В технологическом комплексе добычи полезных ископаемых открытым способом на долю экскавации приходится до 40 % общих расходов [7].
В России исторически сложилась сильная школа, которую создали крупные ученые и разработчики, занимавшиеся (и занимающиеся в настоящее время) проектированием машин с механическим и электромеханическим приводами. С 70-х годов прошлого века в стране ведутся также разработки мощных гидравлических экскаваторов.
В условиях постоянного увеличения объемов земляных работ и ужесточения требований к качеству их выполнения огромное значение приобретает задача совершенствования методов проектирования землеройной техники. Одним из важнейших шагов на пути ее решения являются исследования, направленные на совершенствование расчетов нагрузок на звенья пространственной кинематической цепи «платформа – стрела – рукоять – ковш» в течение рабочего цикла. Точность проектного расчета элементов рабочего оборудования современными методами невысока по следующим причинам:
- сложность математического выражения силовых факторов в многозвенной кинематической цепи с большим числом степеней подвижности;
- разнообразие видов выполняемой экскаватором работы;
- неопределенность внешней нагрузки на рабочее оборудование.
Трудами выдающихся отечественных ученых Н.Г. Домбровского, Е.Р. Петерса, А.Н. Зеленина, Ю.А. Ветрова, А.С. Реброва, Р.Ю. Подэрни и др. заложены основы расчета и проектирования землеройной техники. Предложенные ими методы с полным правом могут считаться классическими, и работа Ф.В. Маковеева [3] на настоящий момент представляется логическим завершением этих методов. Большая заслуга в развитии методик проектирования и в разработке систем управления приводами экскаваторов принадлежит исследованиям В.Р. Кубачека, П.А. Касьянова, Б.А. Носырева, А.П. Комисарова, Н.М. Суслова. На переднем крае находятся такие ученые, как А.В. Крикун, А.П. Побегайло и П.А. Побегайло.
В рамках данного исследования интерес представляют известные методы расчета нагрузок на рабочее оборудование. Сравнение отдельных методик позволяет выявить как их различия, так и общие черты, и в итоге сформулировать задачи дальнейшей работы. Целесообразно рассмотреть наиболее известные фундаментальные труды, отразить новейший результат их развития, после чего дать характеристику современным подходам к расчету и проектированию рабочего оборудования.
Поскольку здесь важно уловить лишь основные принципы построения каждой методики, то нет необходимости в ее подробном анализе. При подходе с позиций теории механизмов и машин [1] достаточно:
- выявить способ представления в расчетах материальной природы (формы, размеров, массы) каждого звена исследуемой кинематической цепи;
- установить, насколько полно отражаются методикой параметры движения (траектории, скорости, ускорения) звеньев в течение рабочего цикла;
- оценить степень точности отражения в расчете действующих на звенья активных сил и сил инерции.
Последнюю операцию удобно осуществить на примере вычисления по рассматриваемой методике какого-либо характерного усилия.
Важно подчеркнуть, что расчеты различных видов рабочего оборудования методически идентичны. Следовательно, результаты изучения расчетов прямых лопат вполне правомерно распространить на расчеты обратных лопат.
Классические методы расчета. В основу методики Н.Г. Домбровского [2] положен принцип подобия рабочих органов и условий резания, в соответствии с которым основные линейные параметры рабочего оборудования карьерных экскаваторов прямая лопата определяются по общей формуле
![]() (1)
(1)
где Li – величина i-го параметра, м; Ki – эмпирический коэффициент; G – рабочий вес экскаватора, тс.
Коэффициент Ki для каждого параметра выбирается из рекомендуемого диапазона.
Таким образом, в качестве критерия подобия выступает вес экскаватора.
Стрела и рукоять рассматриваются как прямолинейные стержни постоянного сечения, их массы считаются сосредоточенными в центрах масс (центрах тяжести) посередине длины.
Для определения траектории движения используется основной вид работы – забой. Стрела остается неподвижной и наклоненной к горизонту под углом ρ, зависящим от высоты оси напорного вала Ннап.вала, рукоять совершает сложное плоское движение, включающее в себя поворот (подъем) и поступательное перемещение (напор), режущая кромка ковша движется по дуге переменного радиуса R
![]() (2)
(2)
где Сmax – максимальная толщина стружки.
Скорости подъема и напора задаются в соответствии с рекомендациями (см. ниже) и зависят от фазы копания (начало, середина, конец).
Рабочее усилие подъема рукояти находят из соотношения
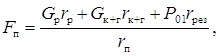 (3)
(3)
где Gр – вес рукояти;Gк+г – вес ковша с грузом; Р01 – усилие на зубьях ковша; rр – расстояние от центра тяжести рукояти до оси напорного вала; rк+г– расстояние от центра тяжести ковша с грузом до оси напорного вала; rрез – плечо усилия Р01;rп – плечо усилия подъема.
В методике НИИтяжмаш (ОАО «Уралмашзавод») [8] для нахождения линейных параметров используется другой критерий подобия, а именно, радиус копания. Будучи размером, он по своей сути соответствует определяемым величинам, что, по-видимому, способствует приближению размеров и масс рабочего оборудования к оптимуму.
Методика Е.Р. Петерса [5] предполагает вычисление усилия подъема по формуле
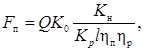 (4)
(4)
где Q – вместимость ковша, м3; K0 – удельная работа резания, кВт/м3; Kн – коэффициент наполнения ковша; Kр – коэффициент разрыхления грунта в ковше; l – перемещение точки приложения усилия подъема на пути копания; ηп – КПД полиспаста канатного подъема рукояти; ηр – КПД рабочего оборудования.
Здесь критерием подобия является работа, затрачиваемая на заполнение ковша.
Исследование [3], как было сказано, представляется наиболее полным и творческим выражением, а может быть, и наивысшим уровнем классических методов расчета. В нем приняты те же допущения о форме и массах звеньев. Скорость подъема рукояти учитывается только для вычисления мощности двигателя и находится как средняя величина по следующей циклограмме: в начале копания (7 % времени) скорость ковша составляет 30 %, в середине (22 % времени) – 60 % и в конце (71 % времени) – 75 % номинальной величины. Аналогичная операция и с той же целью производится со скоростью напора. Усилие на зубьях ковша определяется так же, как в [2]. Приводить какие-либо формулы нагрузок нет необходимости, т.к. они составлены по выше описанным принципам.
Новейшие методы расчета. Недостатки классических подходов к определению геометрических параметров и степени нагруженности рабочего оборудования заставляют исследователей искать пути совершенствования методик расчета. Один из таких путей – рассмотрение системы с позиций аналитической динамики.
В этом плане большой интерес представляет работа [6], основанная на данных, полученных в процессе эксплуатации экскаватора ЭГ-12А. Речь в ней идет о явлениях в гидроприводе, возникающих при опускании ковша в позицию разгрузки. Авторы пишут: «…механическая система ковш – рукоять останавливается не мгновенно, а лишь после полного использования накопленной при движении кинетической энергии… В таком режиме нагружения… возникают явления, … близкие к гидравлическому удару».
Исследуемая система (которую авторы называют «рабочее оборудование – гидропривод», хотя стрела из рассмотрения исключена, а рукоять с ковшом считаются единым звеном) приведена к упрощенной динамической модели. Модель описывается системой из девяти уравнений, в которой одно в числе прочих параметров содержит момент инерции звена, а кинематика представлена не только скоростями, но и ускорениями. В заключительных словах авторы отмечают оценочный характер решения системы.
Среди новейших методов проектирования нельзя не упомянуть их компьютерные разновидности, такие как системы автоматизированного проектирования (САПР). В.П. Павлов, Н.Н. Живейнов и Г.Н. Карасев [4] методику расчета, предназначенную для использования в САПР экскаватора, построили на вероятностно-статистических моделях, которые авторы получили путем обработки практических данных в соответствии с теорией вероятностей и математической статистикой. Назначение САПР – оптимизация одноковшовых экскаваторов по критерию минимума приведенных затрат на эксплуатацию.
Статистически обработан перечень из 24 основных параметров, полученных как отношение фактической величины к массе экскаватора; объем выборки по каждому параметру – от 45 до 118 значений. Построены линии регрессии. Корреляционное отношение в зависимости от параметра колеблется в пределах 0,67…0,96 (самое высокое – для массы ковша).
Для кинематического анализа рабочего оборудования сформирован матричный математический аппарат. Он позволяет рассчитать геометрию рабочего оборудования. Собственно кинематика ограничивается скоростями, ускорения звеньев не рассматриваются.
Соответственно и параметры рабочего оборудования определяются без учета инерционных нагрузок. Единственная задача, при решении которой учитывается среднестатистический момент инерции, – учет углового ускорения при повороте платформы. Силовой анализ производится для нескольких характерных положений рабочего оборудования. Он весьма полезен при решении задач обеспечения устойчивости и вычисления максимальной силы на ковше по условию предотвращения сдвига экскаватора.
Характерные черты известных методов расчета. В классических методиках, прежде всего, обращают на себя внимание предельные упрощения формы стрелы, рукояти и ковша, а также практическое отсутствие динамического анализа. Все это, как было сказано выше, вызвано сложностью расчета динамики многозвенной кинематической цепи с большим числом степеней подвижности.
Вносимые по необходимости в расчет упрощения формы звеньев, допущения, касающиеся характера движений, точек приложения сил и т.д. приводят к значительным погрешностям, в отдельных случаях ставящим под сомнение конечные результаты. Необходимость сохранения работоспособности оборудования в случае вероятного превышения нагрузками их расчетных значений требует введения различных повышающих коэффициентов типа завышенных запасов мощности и прочности. Единственная возможность в таких условиях гарантировать работоспособность техники – построение методов расчета на практических данных, полученных из опыта эксплуатации.
Ограниченность такого подхода очевидна. Как справедливо отмечено в [3], существенным недостатком метода, построенного на статистических данных, является консервативность, обусловленная, во-первых, отсутствием аппарата оперативного отслеживания новшеств, вносимых в технологию экскавации, и, во-вторых, вынужденным копированием уже известных аналогов при проектировании новых машин. Следует добавить, что несовершенство кинематического расчета не позволяет учесть нагрузки, возникающие в периоды неустановившегося движения рабочего оборудования. Вероятно, это одна из причин, по которым конструкторы, использующие классические методики, в качестве основного способа повышения производительности рассматривают увеличение вместимости ковша, а не уменьшение длительности цикла.
Увеличение скоростей движения при сохранении прежней длительности переходных периодов сопровождается повышением ускорений и, как следствие, сил и моментов сил инерции, действующих на звенья кинематической цепи. Инерционные составляющие начинают играть заметную роль в системе сил, приложенных к рабочему оборудованию. Возникает необходимость учета динамики как в прочностных расчетах, так и для определения выходных параметров приводов и оценки энергопотребления, что косвенно подтверждает работа [4]. Известно, что около 70 % энергозатрат стрелоподъемного механизма гидравлического экскаватора обратная лопата приходится на подъем рабочего оборудования. Очевидно, повышение скоростей подъема приведет к росту потребления энергии, и он окажется настолько существенным, что не учитывать это обстоятельство будет уже нельзя.
В исследованиях, посвященных совершенствованию методов расчета, предпринимаются попытки более подробного силового анализа рабочего оборудования. Однако при их изучении создается впечатление, что авторы испытывают слишком сильное влияние классического подхода. Используются те же допущения относительно формы и масс звеньев, решаются задачи, как правило, применительно к нескольким характерным положениям стрелы и рукояти или к их перемещению в одной плоскости, а иногда и вообще один конкретный случай нагружения (например, упор ковша в непреодолимое препятствие).
В последнее время все большее внимание уделяется методам математического моделирования и САПР. Кроме того, что компьютерные (в том числе виртуальные) модели позволяют значительно расширить рамки проектирования, они также помогают качественно представить изменение нагрузок на рабочие органы в процессе экскавации. Но адекватность виртуальной модели зависит от точности базовой математической модели, которая на настоящий момент невысока.
Очень показателен подход, принятый в [4]. Авторы используют все ту же статистическую основу проектирования, но развивают математический аппарат. Суть метода сводится к выбору наиболее совершенной конструкции из ряда несовершенных. Бесспорно, смысл в этом есть. Но очевидно также и то, что методика не дает никакой возможности для разработки технических решений, отличных от представленных выборкой. Другими словами, ей в полной мере присущи недостатки классических методов.
Изучение известных на данный момент методов расчета нагрузок на рабочее оборудование позволяет сделать следующие выводы.
1. Как в классических, так и в новейших методиках стрела и рукоять представлены в виде стержней с массой, сосредоточенной в точке (в центре тяжести).
2. Классические методики оперируют номинальными скоростями движения рабочих органов и их ступенчатым изменением в зависимости от вида работ и стадии копания. Значение скорости принимается из предписанного диапазона. График ее изменения устанавливается на основе статистических исследований. Ускорения не рассматриваются.
Новейшие методики, в основном благодаря использованию компьютерного моделирования, позволяют выполнить полный кинематический анализ процесса копания.
3. В классических методиках активные силы задаются статистически. Динамика рабочего оборудования в процессе копания не рассматривается.
Авторами новейших методик предпринимаются попытки динамического расчета рабочего оборудования применительно к конкретным операциям.
Все вышеизложенное приводит к заключению, что одним из важнейших шагов на пути к созданию новых конструкций экскаваторов следует считать совершенствование методики определения нагрузок на звенья пространственной кинематической цепи «платформа – стрела – рукоять – ковш» в течение рабочего цикла за счет построения уточненной математической модели процесса экскавации.
Уточненная математическая модель позволит не только повысить производительность, но и сделать результаты расчета потребных выходных параметров приводов более достоверными, минимизировать массогабаритные показатели рабочего оборудования и в конечном итоге повысить надежность и экономичность экскаватора.
Рецензенты:
Готлиб Б.М., д.т.н., профессор, заведующий кафедрой «Мехатроника» ФГБОУ ВПО «Уральский государственный университет путей сообщения» Министерства образования и науки Российской Федерации, г. Екатеринбург;
Залазинский А.Г., д.т.н., профессор, заведующий лабораторией системного моделирования, Федеральное государственное бюджетное учреждение науки Институт машиноведения Уральского отделения Российской академии наук, г. Екатеринбург.



