Сложные динамические объекты, как правило, являются нелинейными, многосвязными и многофункциональными – в процессе их функционирования изменяются динамические свойства как самих сепаратных подсистем, так и связей между ними на различных режимах работы [2]. Таким образом, для обеспечения требований по управляемости современные системы автоматического управления СДО необходимо разрабатывать в классе многосвязных систем автоматического управления (МСАУ).
Основная трудность при проектировании МСАУ СДО заключается в обеспечении устойчивости и желаемого качества функционирования многосвязного объекта управления на различных режимах. Удовлетворить столь сложным техническим требованиям могут, в частности, МСАУ, реализующие логические законы управления.
Логические регуляторы берут на себя функции анализа текущего поведения объекта управления и выработки на основе логического закона сигнала управления. Использование логических регуляторов значительно улучшает динамические и статические свойства системы [3]. Основной задачей, связанной с применением логических регуляторов, является разработка логического закона управления, формирующего сигнал управления с учетом структурных и параметрических особенностей объекта управления. Поэтому задача синтеза логических законов управления, позволяющих согласовать сепаратные подсистемы с учетом их взаимосвязи, является актуальной.
В данной статье предлагается новый логический закон управления, новизна которого, в отличие от существующих аналогов, заключается в формировании логической связи между сепаратными подсистемами в составе МСАУ СДО для обеспечения стабилизации и согласования их динамики.
Постановка задачи
Анализ современных исследований в области логического управления СДО показывает, что существуют различные подходы к решению этой проблемы, однако, как правило, они не учитывают влияние перекрестных связей на динамику многосвязного объекта управления.
В контексте нечеткого логического управления предложены многомерные логические регуляторы, основанные на реализации правил логического вывода, выраженных в как нечетких [6], так и в четких термах [1]. Зарубежными авторами предложены нечеткие логически регуляторы для управления нелинейными многосвязными объектами [9]. Однако синтез продукционных правил для управления многосвязным объектом, которые были бы адекватны на всем диапазоне функционирования, невероятно сложен, так как на различных режимах работы структура и динамические параметры объекта управления могут существенно изменяться. Такие структурно-параметрические изменения приводят к значительному изменению характера поведения объекта управления и требует соответствующих изменений продукционных правил. Также, для данного класса регуляторов не разработаны точные методы проверки устойчивости, но есть попытки адаптации классических аналитических подходов [4].
Широкое распространение как в отечественной [3, 5, 7], так и в зарубежной [8, 10] литературе получили системы с переключением коэффициентов передачи либо в прямой цепи, либо в цепи обратной связи. Переключение в таких системах происходит при определенных соотношениях координат системы, которые определяются логическим законом управления [3]. Однако данные логические законы управления не учитывают взаимовлияние сепаратных подсистем, что характерно для МСАУ СДО.
В статье рассматриваются гомогенные МСАУ, состоящие из идентичных сепаратных подсистем. Первые исследования гомогенных многосвязных систем были вызваны развитием энергосистем и крупных электрических станций. Теория гомогенных МСАУ берет свое начало в работах А. А. Красовского, В.Т. Морозовского. Целью управления такими объектами является координация и согласование работы всех сепаратных подсистем. Для достижения данной цели необходимо разработать логический закон управления, формирующий на основе анализа динамики многосвязного объекта управления логические связи между сепаратных подсистем с целью их стабилизации и согласования.
Логический закон управления связями
Проведем синтез логического закона управления, формирующего логическую корректирующую связь ε̅i(t) на основе анализа влияния динамики j-x (j=1…n, j ≠ i) сепаратных подсистем на динамику собственной i-й (i=1…n) подсистемы. Структурная схема данного логического закона управления представлена на рис. 1, где εi(t) – ошибка в i-й подсистеме; ε̅i(t) – корректирующая ошибка, сформированная с учетом влияния динамики j-х подсистем; εi0(t) – собственная ошибка в i-й подсистеме.
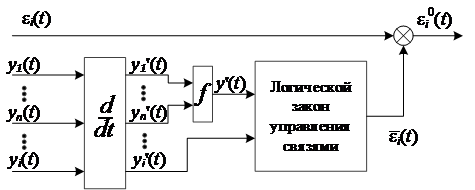
Рис. 1. Структурная схема логического регулятора
Влияние перекрестных связей на качество функционирования сепаратных подсистем в составе МСАУ СДО можно оценить на основе анализа динамики выходных координат. Когда выходные координаты i-й и j-й подсистемы изменяются в противоположных направлениях (что соответствует yi'(t)yj'(t) < 0), то подсистемы не скоординированы между собой и «мешают» друг другу в достижении цели функционирования. Для их координации необходимо форсировать собственную i-ю подсистему созданием положительной связи по динамики yj'(t) j-й подсистемы с некоторым коэффициентом K.
В случае, когда выходные координаты i-й и j-х подсистем изменяются в одном направлении (что соответствует yi'(t)yj'(t) ≥ 0), то подсистемы не согласованы между собой и необходимо сравнивать их абсолютные скорости движения. Если абсолютная скорость |yi'(t)| изменения i-й подсистемы больше абсолютной скорости |yj'(t)|, то i-я подсистема опережает j-ю подсистему и необходимо её замедлять созданием отрицательной связи по динамики yj'(t) j-й подсистемы с некоторым коэффициентом K.
Рассмотрим МСАУ СДО, состоящую из n сепаратных подсистем. Каждая подсистема, на основе сформированного по заданному критерию совокупного влияния j-х подсистем через перекрестные связи, должна принимать решение о формировании положительной или отрицательной связи для координации и стабилизации всей МСАУ СДО в целом. В качестве критерия предлагается использовать следующую функцию:
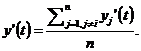
Таким образом, логический закон формирования связей описывается следующей функцией:
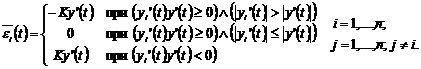
где K – параметр, характеризующий силу формируемой логической связи между i-ой и j-ой сепаратной подсистемой, а y'(t) определяется как:
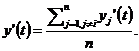
Предлагаемый логический закон на основе анализа динамики многосвязного объекта управления формирует связи между подсистемами, а параметр K определяет силу этой связи.
Проведем анализ качества функционирования МСАУ СДО с предложенным логическим законом формирования связей.
Анализ функционирования МСАУ СДО с предложенным логическим законом формирования связей
Рассмотрим гомогенную трехсвязную систему автоматического управления, структура которой представлена на рис. 2.
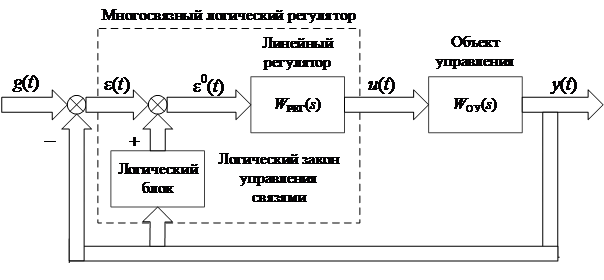
Рис. 2. Структурная схема исследуемой МСАУ СДО
Для описания МСАУ СДО в статье используется подход на основе декомпозиции исследуемой системы на сепаратные подсистемы и многомерный элемент связи между ними [4]. Данный подход позволяет анализировать системы любой размерности и наглядно отображает влияние на устойчивость и качество функционирования МСАУ СДО как динамических свойств сепаратных подсистем, так и связей между ними, что позволяет в полной мере учесть структурно-параметрические особенности данного класса объектов.
В контексте рассматриваемого подхода вводятся такие понятия как индивидуальная характеристика подсистемы, отражающая её динамические свойства, и характеристика многосвязного элемента связи, выражающая силу и характер связи между подсистемами.
В качестве индивидуальной характеристики подсистемы рассмотрим её передаточную функцию в режиме управления – когда подсистема функционирует в изолированном от других подсистем состоянии. Объект управления представляет собой апериодическое звено второго порядка, которое описывается следующей передаточной функцией, где τОУ – постоянная времени объекта управления:
![]()
В качестве линейного регулятора возьмем пропорционально-интегральный регулятор, передаточная функция которого имеет следующий вид:
![]()
Так как исследуемая трехсвязная система является гомогенной, то целесообразно использовать обобщенную характеристику многосвязного элемента связи H для описания действия перекрестных связей относительно действия прямых связей в многосвязном объекте управления [4]:
![]()
где hijk – характеристика связи между группой подсистем.
Рассмотрим характеристику многомерного элемента связи, когда H2 > 0 и H3 > 0. Многомерный элемент связи между сепаратными подсистемами, соответствующий данному характеру связи, описывается следующей матрицей:
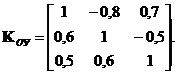
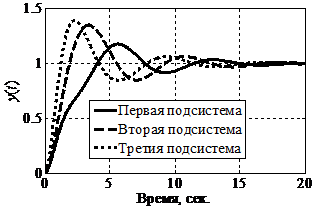
Графики переходных процессов исследуемой системы представлены на рис. 3.
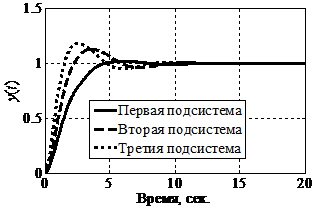
а б
Рис. 3.
Графики переходных процессов в исследуемой системе при H2 > 0 и H3
> 0:
а – без логического регулятора; б – с логическим регулятором
Видно, что в исследуемой системе без логического регулятора наблюдаются значительные колебания переходного процесса. Введение логического регулятор заметно стабилизирует динамики сепаратных подсистем, что приводит к снижению колебательности переходных процессов и уменьшению как перерегулирования, так и времени регулирования.
Рассмотрим характеристику многомерного элемента связи, когда H2 < 0 и H3 > 0. Многомерный элемент связи между сепаратными подсистемами, соответствующий данному характеру связи, описывается следующей матрицей:

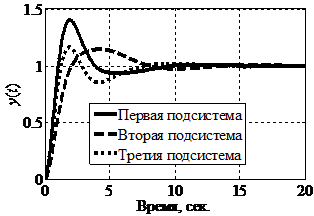
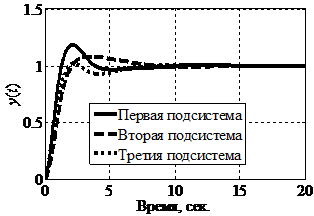
Графики переходных процессов исследуемой системы представлены на рис. 4.
а б
Рис. 4.
Графики переходных процессов в исследуемой системе при H2 < 0 и H3
> 0:
а – без логического регулятора; б – с логическим регулятором
Видно, что в исследуемой системе без логического регулятора наблюдается значительное перерегулирование и «затягивание» переходного процесса. Введение логического регулятора заметно улучшает качество функционирования многосвязной системы, стабилизирует и координирует все сепаратные подсистемы.
Таким образом, преимуществом предложенного логического закона управления является то, что обеспечивается высокое качество управления сепаратной подсистемой за счет введение дополнительных перекрестных связей между регуляторами сепаратных подсистем.
Заключение
Разработана математическая модель закона управления, вырабатывающего корректирующую ошибку ε̅i(t) на основе формирования логических связей между сепаратными подсистемами.
Установлено, что предложенный логический регулятор стабилизирует и согласовывает динамику движения каждой сепаратной подсистемы и существенно улучшается качество переходных процессов, что приводит к значительному улучшению качества функционирования многосвязной системы автоматического управления в целом.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (РФФИ 14-08-97056 р_поволжье_а, 14-08-01019 А, 15-08-01146 А).
Рецензенты:Васильев В.И., д.т.н., профессор, заведующий кафедрой «Вычислительная техника и защиты информации» ФБГОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа;
Мунасыпов Р.А., д.т.н., профессор, заведующий кафедрой «Мехатроннные станочные системы» ФБГОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.



