Постановка задачи
Рассмотрим класс механических объектов (систем), представляющих собой совокупность соединенных между собой и движущихся в пространстве твердых тел, динамика которых описывается уравнениями Лагранжа. Большинство объектов относятся именно к этому классу. Для него уравнения динамики могут быть записаны в виде, совпадающем с уравнениями манипуляционного робота[1, 2]:
![]() , (1)
, (1)
где матрица инерции D(q)>0 (положительно-определенная).
Будем предполагать, что управляющее воздействие U формируется многослойной НС. Ее характеристики будут конкретизированы позже.
Введем новые обозначения:
![]()
Тогда уравнение динамики перепишется в виде:
![]() (2)
(2)
Пусть требуется, чтобы обобщенные координаты динамического объекта q1, q2 следовали за предписанной программной траекторией qd1(t), qd2(t). Ошибки слежения обозначим следующим образом:
![]() (3)
(3)
Вначале ограничимся вторым уравнением (2). Целью синтезируемого нейросетевого управления является обеспечение стремления ошибки к нулю.
Алгоритм обучения нейронной сети
Для получения алгоритма обучения многослойной НС воспользуемся методом скоростного градиента, развитым в работах А.Л. Фрадкова[3, 4]. Образуем локальный целевой функционал
![]() . (4)
. (4)
Вычислим производную целевого функционала по времени в силу уравнений системы (2):
![]() . (5)
. (5)
Из уравнений (3) следует:
![]() (6)
(6)
Так как
![]() , (7)
, (7)
из второго уравнения (2) получим:
![]() . (8)
. (8)
Подставим полученное выражение в производную целевого функционала (5):
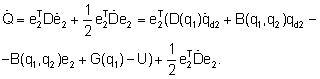 (9)
(9)
Выполнив перекомпоновку слагаемых, получим:
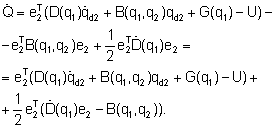 (10)
(10)
Как было показано ранее, последнее слагаемое в (10) равно нулю, поэтому производная целевого функционала равна:
![]() (11)
(11)
Теперь для определенности зададимся конкретными характеристиками многослойной НС. Как будет видно из дальнейшего, это не снижает общности рассуждений при получении алгоритма обучения НС на основе метода скоростного градиента.
Пусть НС имеет один скрытый слой с количеством нейронов H и выходной слой, содержащий m нейронов (m равно размерности вектора e2). Будем также полагать для упрощения выкладок, что в выходных нейронах НС нелинейное преобразование не выполняется и производится лишь суммирование взвешенных сигналов скрытого слоя. Входной вектор содержит N координат.
Обозначим коэффициент передачи по j-му входу i-го нейрона скрытого слоя через wij. Параметр j изменяется в соответствии с размерностью входного вектора: j=1,2…N. Аналогично в соответствии с количеством нейронов скрытого слоя I=1,2…H. Таким образом, коэффициенты передачи для скрытого слоя образуют матрицу размера HxN:
 . (12)
. (12)
Будем считать, что нелинейное преобразование в скрытом слое нейронов выполняется однотипными функциями. Вектор выходных сигналов скрытого слоя НС равен
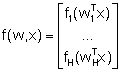 . (13)
. (13)
Здесь wi обозначает i-ю строку матрицы w.
Теперь введем обозначение Wli для коэффициента передачи от i-го нейрона скрытого слоя к l-му выходному нейрону (l=1,2…m). Совокупность этих коэффициентов образует (mxH)-матрицу W.
При описанной структуре многослойной НС ее выходной вектор, представляющий собой сигнал управления в системе, определяется следующим образом:
![]() . (14)
. (14)
Подставим полученное управление в (11):
![]()
В соответствии с методом скоростного градиента вычислим частные производные полученной функции по настраиваемым параметрам. Дифференцирование по матрице W дает
![]() (15)
(15)
Перед тем как записать алгоритм настройки матрицы w, заметим, что для выбранной активационной функции справедливо следующее:
![]() . (16)
. (16)
Введем вспомогательные функции
![]() (17)
(17)
и (HxH)-матрицу
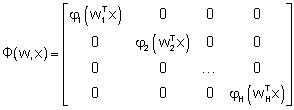 . (18)
. (18)
Непосредственное вычисление дает
![]() . (19)
. (19)
Таким образом, алгоритмы обучения рассматриваемой НС приобретают вид:
![]() , (20)
, (20)
где g – шаг обучения НС.
Процедура обучения НС ведет к минимизации локального целевого функционала (4) и, следовательно, к уменьшению ошибки e2(t). В связи с этим q2(t) с течением времени стремится (в идеальных условиях, асимптотически) к qd2(t):
![]() .
.
Для того чтобы обеспечить следование выхода системы q1(t) за некоторой программной траекторией q*(t), зададимся видом желаемой функции qd2(t):
![]() . (21)
. (21)
При таком выборе вспомогательной функции qd2(t) получаем
![]() , (22)
, (22)
что соответствует неоднородному дифференциальному уравнению с затухающей (или ограниченной) правой частью. При выборе матрицы k, например, диагональной с положительными элементами, обеспечивается асимптотическое слежение за траекторией q*(t) с ограниченной, возможно с нулевой, ошибкой.
Обсудим теперь вопрос о том, какие компоненты должны быть включены во входной вектор многослойной НС. Как следует из выражения (11), выходной вектор нейросетевого регулятора должен компенсировать влияние матричных и векторных функций, зависящих от следующих переменных: ![]() . Поэтому последние и нужно выбрать как составной входной вектор НС.
. Поэтому последние и нужно выбрать как составной входной вектор НС.
При таком общем подходе структура НС оказывается, возможно, излишне сложной из-за большого количества перекрестных связей, что как следствие ведет к увеличению вычислительных затрат на процесс обучения сети.
Для уменьшения структурной сложности нейросетевого регулятора можно предложить путь, состоящий в использовании нескольких более простых многослойных НС, на вход каждой из которых при одновременном обучении подается свой вектор уменьшенной размерности, содержащий только необходимые компоненты. При этом в случае необходимости составляющие выходных векторов могут быть перегруппированы в матрицы. По сути, это означает использование имеющейся информации о структуре математической модели управляемого объекта.
Поясним сказанное на простом примере. Предположим, что решается задача управления двухзвенным манипулятором. В таком случае матрица инерции имеет размерность (2x2) и зависит лишь от обобщенных координат q1=(q11, q12)T. Для ее оценки (показано символом «^») можно применить НС1, приведенную на рис. 1, где в узлах сети располагаются нейроны[5, 6].
Аналогично строится НС2 для оценки матрицы B(q1,q2), причем на вход сети подается составной вектор обобщенных координат q1=(q11, q12)T и обобщенных скоростей q2=(q21, q22)T. Оценивание вектора G(q1) выполняется в НС3, подобно НС1. Тогда с учетом соотношения (11), согласно принципу непосредственной компенсации, управление может быть выбрано в следующем виде[5, 6]:
![]() , (23)
, (23)
где матрица G>0.
Для реализации нейросетевого регулятора вида (23) требуется одновременное обучение сетей НС1-НС3 на основе полученных выше или аналогичных алгоритмов.
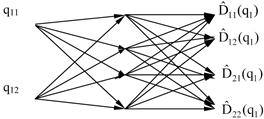
Рис. 1. Нейронная сеть НС1 для оценки матрицы инерции
Работа поддержана Министерством науки и образования Российской Федерации, Государственный контракт 02G25.31.0025.
Рецензенты:
Завьялов В.В., д.т.н., профессор, профессор кафедры Технических средств судовождения, Морской государственный университет имени адмирала Г.И. Невельского, г.Владивосток;
Глушков С.В., дд.т.н., профессор, заведующий кафедрой Автоматических и информационных систем, Морской государственный университет имени адмирала Г.И. Невельского, г. Владивосток.



