Манипулятор, предназначенный для изготовления упаковки с различным профилем поперечного сечения, должен иметь водило (ось), шарнирно закрепленное на раме. В качестве механической модели манипулятора будем рассматривать твердое тело, имеющее неподвижную точку. Поскольку ось водила не совершает вращение вокруг своей оси, то ее положение в пространстве определяется двумя углами Эйлера – углом прецессии ![]() и углом нутации
и углом нутации ![]() . Для управления переносным движением манипулятора (движением оси водила) необходимо задать законы изменения углов
. Для управления переносным движением манипулятора (движением оси водила) необходимо задать законы изменения углов ![]() и
и ![]() . Целесообразно выражать эти углы в функции угла поворота водила
. Целесообразно выражать эти углы в функции угла поворота водила ![]() :
:
![]() ;
; ![]() . (1)
. (1)
Управление переносным движением манипулятора
Рассмотрим управление переносным движением пространственно планетарной роликовой головки для изготовления упаковки квадратного сечения. На рис. 1 показана заданная форма поперечного сечения упаковки.
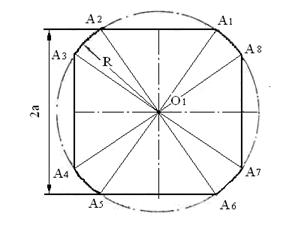
Рис. 1. Заданная форма поперечного сечения.
Для вывода уравнения (1) введем систему координат. Система координат ![]() является инерциальной (связана с рамой манипулятора) и может рассматриваться как неподвижная. Начало координат этой системы помещено в точку шарнирного крепления водила (оси) к раме манипулятора (точка О). Положительное направление осей системы: координатная ось
является инерциальной (связана с рамой манипулятора) и может рассматриваться как неподвижная. Начало координат этой системы помещено в точку шарнирного крепления водила (оси) к раме манипулятора (точка О). Положительное направление осей системы: координатная ось ![]() направлена по оси симметрии проводимого сечения; ось
направлена по оси симметрии проводимого сечения; ось ![]() в горизонтальной плоскости направлена вправо относительно направления проведения сечения; ось
в горизонтальной плоскости направлена вправо относительно направления проведения сечения; ось ![]() направлена перпендикулярно плоскости
направлена перпендикулярно плоскости ![]() . С водилом оси неизменно связана система координат Oxyz с началом в той же точке О; ось Oy совпадает с осью водила. Положение системы координат Oxyz относительно системы
. С водилом оси неизменно связана система координат Oxyz с началом в той же точке О; ось Oy совпадает с осью водила. Положение системы координат Oxyz относительно системы ![]() , а следовательно и положение водила, определяется углом
, а следовательно и положение водила, определяется углом ![]() и
и ![]() . Направление осей симметрии Oxyz совпадает с направлением соответствующих осей симметрии системы в момент, когда ось водила совпадает с осью симметрии сечения на упаковке. Кроме того, введем систему координат O1x1y1z1 с началом в точке О1, являющейся концом водила. Оси этой системы параллельны соответствующим осям системы Oxyz, и, наконец, вводится еще одна система координат
. Направление осей симметрии Oxyz совпадает с направлением соответствующих осей симметрии системы в момент, когда ось водила совпадает с осью симметрии сечения на упаковке. Кроме того, введем систему координат O1x1y1z1 с началом в точке О1, являющейся концом водила. Оси этой системы параллельны соответствующим осям системы Oxyz, и, наконец, вводится еще одна система координат ![]() , неизменно связанная с пространственно планетарной роликовой головкой и вращающейся вокруг оси водила пространственно планетарной роликовой головки с угловой скоростью, равной
, неизменно связанная с пространственно планетарной роликовой головкой и вращающейся вокруг оси водила пространственно планетарной роликовой головки с угловой скоростью, равной ![]() .
.
Пусть водило пространственно планетарной роликовой головки будет повернуто на угол ![]() положительный, при условии, что он отсчитывается против часовой стрелки, если смотреть с положительного направления координатной оси Oy. Для того чтобы в новом положении водила ролики находились в контакте с заготовкой упаковки, необходимо перевести водило в определенное положение, повернув его вокруг точки О, причем углы
положительный, при условии, что он отсчитывается против часовой стрелки, если смотреть с положительного направления координатной оси Oy. Для того чтобы в новом положении водила ролики находились в контакте с заготовкой упаковки, необходимо перевести водило в определенное положение, повернув его вокруг точки О, причем углы ![]() и
и ![]() , определяющие новое положение манипулятора, должны быть такими, чтобы ролики находились на линии аА. Очевидно, перевод манипулятора в требуемое положение можно осуществить различными способами. Рассмотрим два из них. 1. При повороте манипулятора на произвольный угол его положение должно быть таким, чтобы прямая
, определяющие новое положение манипулятора, должны быть такими, чтобы ролики находились на линии аА. Очевидно, перевод манипулятора в требуемое положение можно осуществить различными способами. Рассмотрим два из них. 1. При повороте манипулятора на произвольный угол его положение должно быть таким, чтобы прямая ![]() пересекала ось ОО1. 2. Траектория движения конца оси манипулятора представляет собой окружность, центр которой расположен на оси заготовки упаковки (рис. 2) и угол поворота радиуса этой окружности связан с углом поворот водила в соотношении:
пересекала ось ОО1. 2. Траектория движения конца оси манипулятора представляет собой окружность, центр которой расположен на оси заготовки упаковки (рис. 2) и угол поворота радиуса этой окружности связан с углом поворот водила в соотношении: ![]() .
.
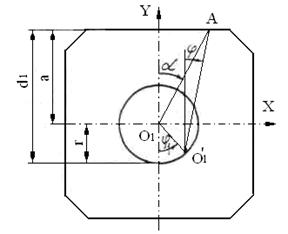
Рис. 2.
Знак «минус» указывает, что вращение водила О1А и радиус окружности ![]() направлены в противоположные стороны.
направлены в противоположные стороны.
Выпишем координаты точки А в системе ![]() :
: ![]() ;
; ![]() ;
; ![]() . В системе
. В системе ![]() координаты точки А будут:
координаты точки А будут: ![]() ;
; ![]() ;
; ![]() .
.
Теперь определим координаты точки А в системе ![]() . Поскольку система координат
. Поскольку система координат ![]() получается путем поворота осей системы
получается путем поворота осей системы ![]() относительно оси
относительно оси ![]() на угол
на угол ![]() и последующего поворота системы относительно оси
и последующего поворота системы относительно оси ![]() на угол
на угол ![]() , то координаты точки А в системе
, то координаты точки А в системе ![]() будут:
будут: ![]() ;
; ![]() ;
; ![]() , где
, где ![]() ;
; ![]() ,
, ![]() =1, 2, 3 – косинусы углов между соответствующими осями. Значения косинусов:
=1, 2, 3 – косинусы углов между соответствующими осями. Значения косинусов: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Таким образом, координаты точки А в системе ![]() :
:
![]() ;
;
![]() ;
;
![]() , (2)
, (2)
где L – расстояние от точки шарнирного закрепления оси манипулятора на раме до точки пересечения оси водила с плоскостью, в которой вращается водило пространственно планетарной роликовой головки.
Формулы (2) остаются справедливыми для любого значения угла поворота водила ![]() . Для вывода уравнений, связывающих углы
. Для вывода уравнений, связывающих углы ![]() ,
, ![]() ,
, ![]() , необходимо последовательно рассмотреть выделенные на рис. 1 участки профиля упаковки, налагая определенные условия на координаты
, необходимо последовательно рассмотреть выделенные на рис. 1 участки профиля упаковки, налагая определенные условия на координаты ![]() и
и ![]() , определяющие заданную форму поперечного сечения.
, определяющие заданную форму поперечного сечения.
Участок А1А2. Чтобы упаковка имела форму поперечного сечения в виде квадрата, необходимо выполнение условий: ![]() ;
; ![]() , что на основании (2) приводит к системе двух уравнений:
, что на основании (2) приводит к системе двух уравнений:
![]() (3)
(3)
где ![]() – угол обхода профиля поперечного сечения упаковки.
– угол обхода профиля поперечного сечения упаковки.
Рассуждая аналогично, запишем для других участков профиля условия, налагаемые на координаты ![]() и
и ![]() , и получаемые из (2) уравнения.
, и получаемые из (2) уравнения.
Участок А3А4: ![]() ;
; ![]() ;
;
![]() (4)
(4)
Участок А5А6: ![]() ;
; ![]() ;
;
![]() (5)
(5)
Участок А7А8: ![]() ;
; ![]() ;
;
![]() (6)
(6)
Участки А2А3, А4А5, А6А7, А8А1 – дуги окружности радиуса R, для них условия, налагаемые на координаты ![]() и
и ![]() (
(![]() ;
; ![]() ), и уравнения, получаемые из (2), будут одинаковыми:
), и уравнения, получаемые из (2), будут одинаковыми:
![]() (7)
(7)
Для нахождения зависимости угла ![]() , входящего в уравнения (3)-(7), от угла
, входящего в уравнения (3)-(7), от угла ![]()
![]() (8)
(8)
воспользуемся условием, что при повороте водила на произвольный угол прямая ![]() должна пересекать ось ОО1 и, следовательно, прямые
должна пересекать ось ОО1 и, следовательно, прямые ![]() и аО1 располагаются в одной плоскости. Запишем уравнения прямых
и аО1 располагаются в одной плоскости. Запишем уравнения прямых ![]() и аО1 на основании формул прямой линии, проходящей через две заданные точки:
и аО1 на основании формул прямой линии, проходящей через две заданные точки:
уравнение прямой ![]()
![]() ;
;
уравнение прямой аО1
![]() .
.
Условие принадлежности прямых ![]() и аО1 одной плоскости:
и аО1 одной плоскости:
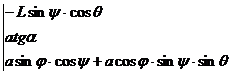
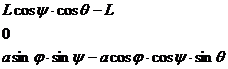
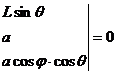 .
.
Раскрыв определитель и выполнив необходимые преобразования, получим уравнение
![]() , (9)
, (9)
которое в соответствии с уравнениями (3)-(7) позволяет определить закон движения манипулятора.
Будем отсчитывать углы ![]() и
и ![]() в этом случае так же, как и при первом способе перемещения водила. Поэтому координаты точки контакта роликов с профилем поперечного сечения упаковки А выражаются по формулам, аналогичным (2), с той разницей, что длина водила О1А в этом случае отлична от а. Обозначим ее через d1:
в этом случае так же, как и при первом способе перемещения водила. Поэтому координаты точки контакта роликов с профилем поперечного сечения упаковки А выражаются по формулам, аналогичным (2), с той разницей, что длина водила О1А в этом случае отлична от а. Обозначим ее через d1: ![]() ;
; ![]() , а координаты конца оси водила О1 выражаются так:
, а координаты конца оси водила О1 выражаются так: ![]() ;
; ![]() .
.
Так как конец оси водила О1 описывает окружность, радиус которой r, то ![]() ;
; ![]() , откуда, учитывая свойства четности и нечетности соответствующих функций, получаем соотношения для выражения углов
, откуда, учитывая свойства четности и нечетности соответствующих функций, получаем соотношения для выражения углов ![]() и
и ![]() через угол поворота водила
через угол поворота водила ![]() :
:
![]() ;
; ![]() . (10)
. (10)
Профили поперечного сечения упаковки для различных значений k в уравнении ![]() представлены на рис. 3.
представлены на рис. 3.
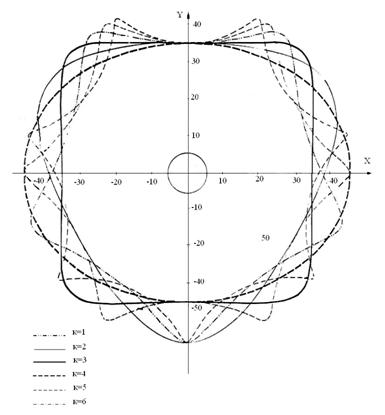
Рис. 3.
Вывод
Найденные законы переносного движения исполнительного органа являются исходными данными для разработки системы автоматического управления пространственно планетарной роликовой головкой при изготовлении упаковки различного сечения.
Рецензенты:
Жизняков А.Л., д.т.н., профессор, первый зам. директора, зав. кафедрой систем автоматизированного проектирования, МИ (филиал) ВлГУ, г. Муром.
Орлов А.А., д.т.н., профессор, зам. директора по развитию электронного обучения и дистанционных образовательных технологий, зав. кафедрой физики и прикладной математики, МИ (филиал) ВлГУ, г. Муром.



