Сторонники подхода к рассмотрению поведения стержневых систем, подверженных внезапному удалению связей как совершающих свободные колебания с начальными условиями, сталкиваются, в первую очередь, с очень жесткими границами применимости этого метода, вызванными физическими характеристиками материала несущих конструкций. Действительно, в подавляющем большинстве реально существующих конструкций, не рассчитанных на сопротивление каким–либо экстремальным воздействиям, запас прочности стремится к минимуму, следовательно, при внезапном изъятии из системы связи, усилия в соседних элементах после перераспределения почти наверняка превысят предел упругости. Как следствие, необходимо рассматривать уже нелинейные колебания, в которых восстанавливающие силы помимо времени зависят и от обобщенной координаты. Настоящая статья посвящена поиску аналитического решения задачи о свободных поперечных колебаниях балки, несущей сосредоточенную массу, упругая характеристика которой близка к низкоуглеродистой стали.
Задание упругой характеристики
В качестве выражения, описывающего упругие свойства материала, примем полином n–ой степени вида[5]:
![]() (1)
(1)
Для стали, одинаково работающей на растяжение и сжатие вид графика будет симметричным относительно нуля, а коэффициенты полинома при неизвестных в четной степени ничтожно малы по сравнению с коэффициентами при степенях 1, 3, 5… Таким образом, выражение упругой характеристики принимает вид:
![]() (2)
(2)
В качестве примера ниже представим диаграмму растяжения–сжатия стали (рис.2), заданную в виде линейного графика (![]() ) и двух полиномов 3–й (
) и двух полиномов 3–й (![]() ) и 5–й (
) и 5–й (![]() )) степени. Значения прогиба и соответствующие напряжения близки к значениям, соответствующим расчетной схеме, представленной на рис.1.
)) степени. Значения прогиба и соответствующие напряжения близки к значениям, соответствующим расчетной схеме, представленной на рис.1.
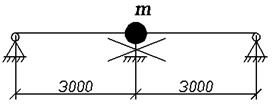
Рис.1
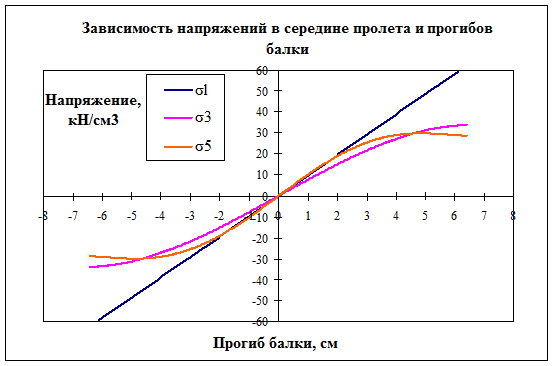
Рис. 2
Отметим, что в настоящей статье абсолютные значения напряжений, прогибов и усилий в балке приняты приблизительно, не принимая во внимание явления, сопряженные с поведением стали в упруго-–пластической зоне, как–то: явление гистерезиса, динамическое упрочнение, уменьшение площади сечения. Главным предметом изучения является получение уравнений колебания балки с нелинейной упругой характеристикой. Численные значения приводятся исключительно для получения наглядных результатов, порядок которых близок к реальным с учетом вышеприведенных оговорок.
Границами применимости каждого из нелинейных графиков условимся принимать значение абсциссы, при которой достигается первый экстремум функции. Так, в нашем случае это 6,414см для полинома 3-й степени и 4,467см для полинома 5-й степени.
Задача о колебаниях одномассовой балки с нелинейной упругостью, описываемой полиномом 3-й степени
Принципиальное отличие рассматриваемого случая от линейной постановки заключается в том, что в уравнение равновесия помимо сил инерции и упругих сил балки должен входить также вес массы. В теории линейных колебаний, как правило, влияние собственного веса опускают в связи с тем, что ни амплитуда, ни частота колебаний не зависят от веса балки и начальных условий, а при необходимости определения величины усилий в сечениях можно использовать принцип независимости действия сил.
Как известно, в нелинейной постановке принцип суперпозиции не выполняется, и действие собственного веса необходимо учитывать в основном дифференциальном уравнении.
Рассмотрим балку на двух опорах, несущую одну сосредоточенную массу. Отклоним массу на небольшую величину и составим уравнение всех сил, действующих на систему:
![]() , (3)
, (3)
где F(x) – упругая характеристика, P=Const – собственный вес массы m.
Упругую характеристику опишем полиномом 3–й степени вида:
![]() ,
,
где ![]() – некий малый параметр.
– некий малый параметр.
В литературе широко описано применение метода малого параметра Пуанкаре [4, c.22; 3, c180] для решения классических задач нелинейной механики, например, осциллятора Дуффинга [2, с.122].Для решения более широкого круга задач будем учитывать константу B, являющуюся множителем при x.
В решении ограничимся рассмотрением только членами при µ первого порядка.
Разделив на m и сгруппировав слагаемые, получим:
![]() , где (4)
, где (4)
![]() ;
; ![]() ;
; ![]() ;
;
Аналитическое решение методом малого параметра разделено на множители и приведено в табл.1.
Таблица 1
Частоты колебаний и перемещения массы при учете разных степеней малого параметра. Упругая характеристика задана полиномом 3–й степени
|
Порядок малого параметра |
Круговая частота, ωn |
Координата, xn |
|
0 |
|
|
|
1 |
|
|
|
2 |
|
|
Итоговое решение [1, с. 24]:
![]() (5)
(5)
![]() (6)
(6)
В линейной постановке с учетом действия постоянной силы P=Const дифференциальное уравнение, описывающее колебания балки будет иметь вид:
![]() (7)
(7)
А его решение:
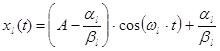 , (8)
, (8)
где ![]() .
.
Для наглядного представления и количественной оценки рассмотрим пример, описанный в начале (рис.1).
Упругая характеристика балки, описанная функцией ![]() (кН):
(кН):
F3(x)=14,817x-0,116x3
Собственный вес (кН):
P=Const=46,6 кН
Сумма всех действующих сил:
![]()
Итоговый вид нелинейного дифференциального уравнения:
![]()
Соответственно, значения коэффициентов уравнения (4):
α=-981,053 β=311,937 δ=2,442 μ=1
В линейной постановке упругая характеристика балки описана функций ![]() . (см. рис.1). Её вид:
. (см. рис.1). Её вид:
Fl(x)=9,719x
Итоговый вид нелинейного дифференциального уравнения:
![]()
Перемещения массы при разных значениях начального отклонения (A) и учете слагаемых при разных степенях малого параметра приведены в табл. 3. На графиках представлены два случая – при отклонениях, вызывающих колебания, близкие к линейным (рис.3а ), и сильно нелинейные колебания (рис.3б).
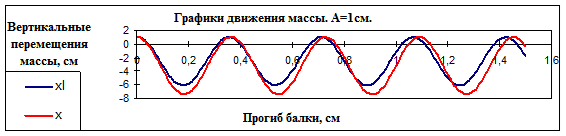
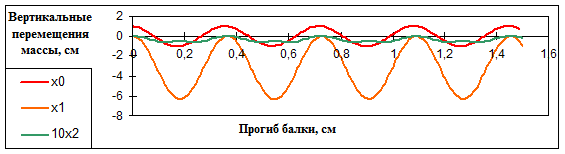
Рис. 3а
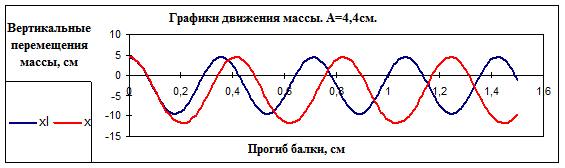
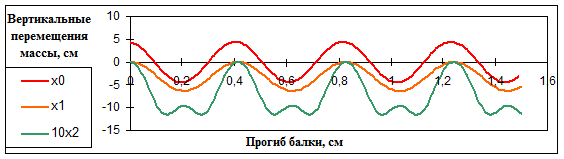
Рис.3б.
Задача о колебаниях одномассовой балки с нелинейной упругостью, описываемой полиномом 5–й степени
Вернемся к диаграмме растяжения–сжатия, представленному на рис.2. Очевидно, что аппроксимация полиномом более высокой степени дает более точный результат и для повышения точности метода следует по–возможности использовать полином 5–й степени.
Уравнение (4) в этом случае принимаем вид:
![]() (9)
(9)
Аналитическое решение методом малого параметра приведено в табл.2.
Таблица 2
Частоты колебаний и перемещения массы при учете разных степеней малого параметра. Упругая характеристика задана полиномом 5–й степени
|
Порядок малого параметра |
Круговая частота, ωn |
Координата, xn |
|
0 |
|
|
|
1 |
|
|
|
2 |
|
|
*![]()
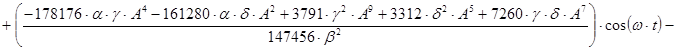
![]()
![]()
![]()
![]()
Значения ω и x(t) определяются по уравнениям (5) и (6), соответственно.
Значения коэффициентов, входящих в уравнение (9) и соответствующих кривой, изображенной на рис.2:
α=-981,053 β=414,956 δ=9,009 γ=-0,008 μ=1
Перемещения массы при разных значениях начального отклонения (A) и учете слагаемых при разных степенях малого параметра приведены в табл. 3. На графиках представлены два случая – при отклонениях, вызывающих колебания, близкие к линейным (рис.4а ), и сильно нелинейные колебания (рис.4б):
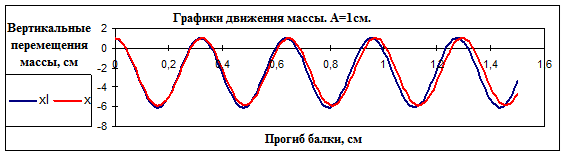
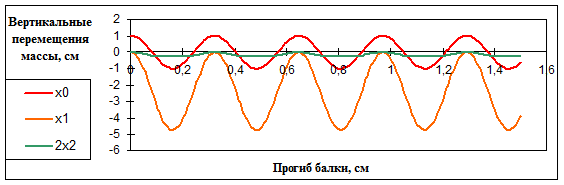
Рис.4а.
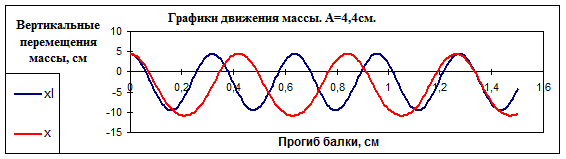
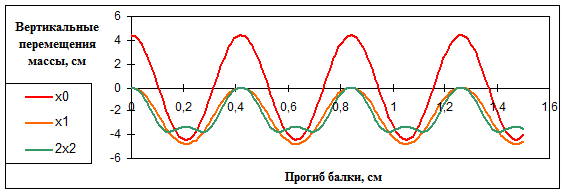
Рис. 4б
Сводные таблицы расчетов
В таблицах ниже xl, x3 и x5 – перемещения массы в случае задания упругой характеристики балки функциями σl, σ3, σ5, соответственно; ωl, ω3 и ω5 – круговые частоты при σl, σ3, σ5.
Результаты приведены для начальных отклонений A, соответствующих упругим (A=1см), близким к пределу текучести (A=2см) и лежащим за пределом текучести (A=4,4см) напряжениям в балке.
Таблица 3
Перемещения массы при учете разных степеней малого параметра. Сравнение балки с линейной и нелинейной упругостью
|
Порядок малого параметра |
Min xl |
Min x3 |
|
Min x5 |
|
|
A=1 см |
|||||
|
0 |
6,04126 |
0,99980 |
504 |
0,99948 |
504 |
|
1 |
7,28923 |
17,12 |
5,72671 |
5,49 |
|
|
2 |
7,33841 |
17,68 |
5,82850 |
3,65 |
|
|
A=2 см |
|||||
|
0 |
7,04115 |
1,99973 |
252 |
1,99951 |
252 |
|
1 |
8,28938 |
15,06 |
6,72741 |
4,66 |
|
|
2 |
8,48607 |
17,03 |
7,12354 |
1,16 |
|
|
A=4,4 см |
|||||
|
0 |
9,44089 |
4,39989 |
114,6 |
4,39998 |
114 |
|
1 |
10,6899 |
11,68 |
9,12844 |
3,42 |
|
|
2 |
11,6417 |
18,90 |
10,7742 |
12,37 |
|
Таблица 4
Круговые частоты колебаний при учете разных степеней малого параметра. Сравнение балки с линейной и нелинейной упругостью
|
Порядок малого параметра |
Min ωl |
Min ω3 |
|
Min ω5 |
|
|
A=1 см |
|||||
|
0 |
6,0413 |
17,6617 |
10,474 |
20,3705 |
3,257 |
|
1 |
17,6099 |
10,737 |
20,206 |
2,422 |
|
|
2 |
17,2837 |
12,390 |
19,432 |
1,498 |
|
|
A=2 см |
|||||
|
0 |
19,728 |
17,6617 |
10,474 |
20,3705 |
3,257 |
|
1 |
17,4543 |
11,525 |
19,727 |
0,007 |
|
|
2 |
16,8007 |
14,839 |
18,239 |
7,546 |
|
|
A=4,4 см |
|||||
|
0 |
19,728 |
17,6617 |
10,474 |
20,3705 |
3,257 |
|
1 |
16,6579 |
15,562 |
17,6197 |
10,687 |
|
|
2 |
15,1897 |
23,005 |
14,9470 |
24,234 |
|
Отметим несколько закономерностей:
1. Необходимо учитывать члены, степень малого параметра при которых не меньше единицы.
2. При небольших начальных отклонениях особенно сильно проявляется погрешность использования полинома 3–й степени. Так, перемещения массы при начальном отклонении 1 см в линейной постановке должно быть максимально приближено к нелинейной. При использовании упругой характеристики σ3 погрешность составляет 17,12% – 17,68% , тогда как для σ5 эта величина 5,49% – 3,65%. Похожая картина и для отклонения 2см, также соответствующего упругой работе материала.
3. По мере роста начального отклонения существенно растет значимость использования членов при высших степенях малого параметра.
Следует обратить внимание, что в указанных примерах причиной возникновения колебаний является действие постоянного веса массы и начальное отклонение от положения статического равновесия, причем величина начального отклонения в представленных примерах целенаправленно принята независящей от веса.
При реальном расчете балки с нелинейной упругой характеристикой, несущей сосредоточенную массу и подверженной внезапному удалению связи, величина начального отклонения будет фиксированной. Алгоритм расчета на внезапное удаление связи будет следующим:
-
Статический расчет системы до удаления связи. Определение смещения массы Δ0.
-
Выбор аппроксимирующей функции для упругой характеристики балки, запись коэффициентов α, β, δ, γ, μ.
-
Статический расчет физически нелинейной системы после удаления связи. Определение смещения массы Δ1.
-
Определение величины начального смещения как разности величин Δ1 и Δ0.
-
Подстановка всех величин в уравнения (5) и (6).
Выводы
-
Метод малого параметра Пуанкаре применим для динамического расчета одномассовой балки с нелинейной упругой характеристикой, подверженной внезапному удалению связи, и позволяет аналитически получить решение задачи о собственных колебаниях.
-
Учет нелинейности позволяет в несколько раз расширить границы применимости метода, описанного в [1] за счет роста максимально возможного начального отклонения массы, даже если соответствующие ему напряжения лежат за пределом упругости.
-
Точность решения сильно зависит от функции, описывающей нелинейно–упругую характеристику балки, поиск этой функции является отдельной, довольно трудоемкой задачей.
-
Развитие подхода требует учета явления гистерезиса.
Рецензенты:
Масленников А.М., д.т.н., профессор кафедры Строительной механики, ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург;
Кондратьева Л.Н., д.т.н., профессор, зав. кафедрой Строительной механики, ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург.



