Одной из основных задач вибродиагностики конструкций и машин является разработка диагностических признаков, характеризирующих различные неисправности машин или повреждения конструкций. Экспериментальное определение диагностических признаков связано с большими материальными затратами в силу многообразия как конструкций, так и неисправностей или повреждений. Поэтому большое практическое значение приобретает численное, конечно-элементное исследование динамического поведения конструкций.
В работе [2] приводится обзор работ, посвященных разработке методов и средств вибродиагностики трещин в виде разреза при ее динамическом нагружении. Предлагается кусочно-линейная модель трещины, использующая понятие эквивалентного шарнира.
В рассматриваемой ниже статье в рамках учебного процесса предлагается и исследуется возможность применения Gap-элементов при конечно-элементном анализе в задачах вибродиагностики конструкций с целью обнаружения возникновения и развития в них трещин. При этом конфигурация трещины может быть любой.
Применение Gap-элементов при динамическом нагружении отмечено только в работе [6], где показано, что использование нелинейного Gap-элемента в качестве модели демпфера сухого трения позволяет достаточно точно оценивать эффективность действия демпферных вставок.
При изложении курса "Основы вибродиагностики конструкций и машин" практические занятия и расчетно-графические работы основаны на построении конечно-элементной модели (КЭ-модели) для определения диагностических признаков в виброакустическом сигнале при появлении трещины в конструкции. В качестве объекта выбрана балка-стенка, позволяющая на всех этапах динамического анализа вести тестирование, сравнивая полученные результаты с аналитическими решениями там, где это возможно. Балка-стенка выполнена в виде прямоугольной стальной пластины с размерами ![]() м.
м.
Для оценки достоверности получаемых результатов расчеты выполняются в виде задач-тестов [4], в процессе решения которых студенты осваивают методику динамического анализа. Расчеты выполняются в конечно-элементном пакете, позволяющем производить динамический нелинейный анализ и имеющего элементы спектрального анализа, являющегося теоретической основой вибродиагностики [5]. Каждому студенту выдается индивидуальное задание. Далее рассматривается один из возможных вариантов задания.
В математическом плане поведение упругой конструкции при отсутствии в ней трещин при динамическом нагружении описывается матричным дифференциальным уравнением
![]() , (1)
, (1)
где ![]() - матрицы масс, демпфирования и жесткости соответственно;
- матрицы масс, демпфирования и жесткости соответственно; ![]() - вектор узловых перемещений;
- вектор узловых перемещений; ![]() - вектор узловой нагрузки.
- вектор узловой нагрузки.
При проведении натурного эксперимента и отцифровки аналогового сигнала с помощью аналого-цифрового преобразователя (АЦП) получается файл дискретных вибропараметров (перемещений, скоростей, ускорений в зависимости от типа вибродатчика).
При численном решении уравнения (1) получаются вибропараметры на каждом временном шаге интегрирования. Поэтому шаг интегрирования уравнения (1) должен выбираться из того же условия, что и шаг дискретизации АЦП в натурном эксперименте. Таким образом, при возможном сопоставлении результатов натурного эксперимента с результатами численного расчета необходимо, чтобы шаг дискретизации АЦП в натурном эксперименте равнялся временному шагу при решении уравнения (1).
При проведении как натурного, так и численного эксперимента получаем функцию вибропараметров с ограниченным спектром, поэтому для выбора шага интегрирования уравнения (1) необходимо воспользоваться теоремой Котельникова В.А., которая в формулировке ее автора гласит, что "любую функцию f(t), состоящую из частот от 0 до fc , можно передавать с любой точностью при помощи чисел, следующих друг за другом через 1/2fc секунд" [7]. Таким образом, чтобы аналоговый сигнал с вибродатчика мог быть отцифрован, а затем восстановлен, необходимо и достаточно, чтобы частота дискретизации была больше или равна удвоенной частоте fc аналогового сигнала. Поэтому временной шаг численного решения уравнения (1) должен быть равным не более чем 1/2fc.
Принимая заданный студентам диапазон частот от 0 до ![]() = 5000 рад/сек (fc = 795,775 Гц), получаем, что шаг интегрирования по времени не должен быть более чем Δt = 0,628·
= 5000 рад/сек (fc = 795,775 Гц), получаем, что шаг интегрирования по времени не должен быть более чем Δt = 0,628·![]() сек. При задании диапазона частот учитывалось, что первая частота свободных колебаний линейной конечно-элементной модели (КЭ-модели), представленной на рисунках 1-4, равна 2265 рад/сек.
сек. При задании диапазона частот учитывалось, что первая частота свободных колебаний линейной конечно-элементной модели (КЭ-модели), представленной на рисунках 1-4, равна 2265 рад/сек.
В одной из задач задания студентам требуется определить амплитуду и спектр виброперемещений наблюдаемого узла (где предполагается установка вибродатчика в натурном эксперименте), если прикладываемая нагрузка вызвана мини-электродвигателем с редуктором, число оборотов которого n=3000 об/мин. В редукторе имеется два балансира массой 50 гр. каждый и с эксцентриситетом 40 мм. Массой электродвигателя и редуктора пренебречь. В результате на балку-стенку будет действовать гармонически изменяющаяся во времени сосредоточенная сила с амплитудой 394 Н и круговой частотой ω=314 рад/сек.
Упругая конструкция при отсутствии в ней повреждений является линейной. При прохождении гармонического сигнала через линейный элемент, коим является упругая конструкция, сигнал (отклик) должен оставаться неизменным по форме, приобретая лишь другую амплитуду и начальную фазу [7]. Динамическое поведение линейной КЭ-модели в этом случае описывается линейным матричным дифференциальным уравнением
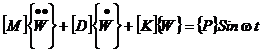 . (2)
. (2)
На рис. 1 приведен отклик 21-го узла и его амплитудный спектр виброперемещений при воздействии гармонической силой ![]() на КЭ-модель, что подтверждает правильность конечно-элементного моделирования.
на КЭ-модель, что подтверждает правильность конечно-элементного моделирования.
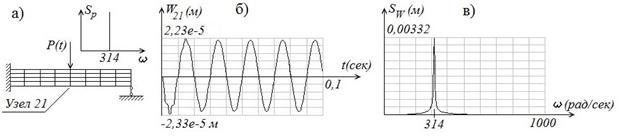
Рис. 1. Прохождение гармонического сигнала через линейную КЭ-модель:
а – нагружение КЭ-модели и спектр приложенной силы; б – виброперемещения 21-го узла; в – амплитудный спектр виброперемещений 21-го узла
При воздействии на линейную КЭ-модель двух гармонических сигналов ![]() результат их воздействия показан на рис. 2.
результат их воздействия показан на рис. 2.
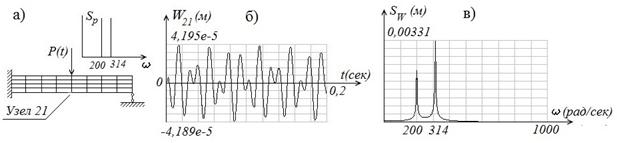
Рис. 2. Прохождение двух гармонических сигналов через линейную КЭ-модель:
а – нагружение КЭ-модели и спектр приложенной силы; б – виброперемещения 21-го узла;
в – амплитудный спектр виброперемещений 21-го узла
При приложении двух гармонических колебаний с близкими частотами ![]() и
и ![]() , удовлетворяющими условию
, удовлетворяющими условию ![]() <<
<<![]() , и
, и ![]() должны наблюдаться биения [5]. На рис. 3 показаны результаты линейного КЭ-моделирования, подтверждающие справедливость этого утверждения. При этом принималось, что
должны наблюдаться биения [5]. На рис. 3 показаны результаты линейного КЭ-моделирования, подтверждающие справедливость этого утверждения. При этом принималось, что ![]() A1=А2=394 Н, ω1=100 рад/сек и ω2=125 рад/сек. Теоретический подсчет периода биений по формуле
A1=А2=394 Н, ω1=100 рад/сек и ω2=125 рад/сек. Теоретический подсчет периода биений по формуле
![]() сек
сек
совпадает с численным экспериментом, результаты которого приведены на рис.3.
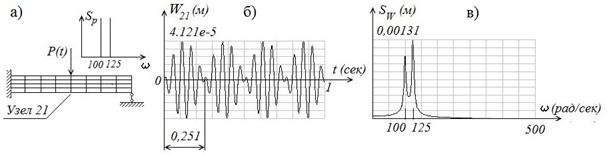
Рис. 3. Прохождение близких по частоте двух гармонических сигналов через линейную КЭ-модель: а – нагружение КЭ-модели и спектр приложенной силы;
б – виброперемещения 21-го узла; в – амплитудный спектр виброперемещений 21-го узла
При аддитивном взаимодействии низкочастотного и высокочастотного гармонического сигнала, временная реализация отклика и его спектра представлена на рис. 4. При этом принималось, что A1=А2= 394 Н, ω1=150 рад/сек и ω2=14 рад/сек.
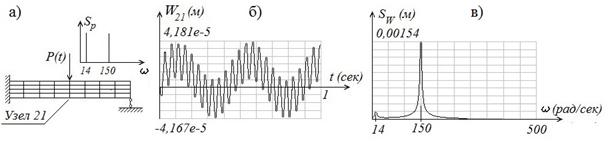
Рис. 4. Прохождение низкочастотного и высокочастотного гармонических сигналов через линейную КЭ-модель: а – нагружение КЭ-модели и спектр приложенной силы; б – вибро-перемещения 21-го узла; в – амплитудный спектр виброперемещений 21-го узла
При появлении трещины конструкция становится нелинейной в силу "дыхания" трещины: при деформации конструкции в направлении закрытия трещины жесткость конструкции равна бездефектному состоянию, при деформации конструкции в направлении раскрытия трещины жесткость мгновенно уменьшается и ее величина зависит от глубины трещины (рис.6). В этом случае динамическое поведение КЭ-модели описывается нелинейным матричным уравнением
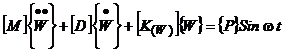 , (3)
, (3)
в котором матрица жесткости является функцией от перемещений узлов КЭ-модели и, следовательно, зависит от времени. "Отслеживать" закрытие и открытие трещины в процессе динамического процесса деформирования КЭ-модели позволяют двухузловые Gap-элементы, работающие на сжатие.
На рис. 5 показан пример конструирования трещины длиной l=(3/4)h при использовании Gap-элементов, т. е. количество Gap-элементов в КЭ-модели зависит от глубины трещины. Поэтому при каждой длине трещины приходится создавать свою КЭ-модель.
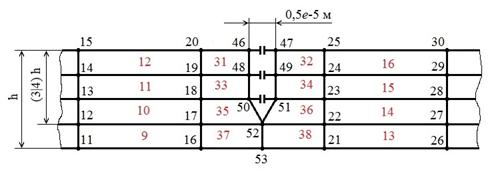
Рис. 5. Моделирование трещины из Gap-элементов
Из теории спектров известно [7], что, если некоторое периодическое колебание P(t) подвергнуть нелинейной операции (такую нелинейную операцию в натурном эксперименте выполняет упругая конструкция, имеющая трещину), то полученное в результате этой операции колебание будет обладать спектром, отличным от спектра P(t) и, как правило, более богатым. Так, например, если первоначальное колебание представляет собой сумму двух синусоид
![]()
![]()
![]() (4)
(4)
и, следовательно, имеет спектр, состоящий из двух спектральных линий, то после нелинейной операции получим в составе колебания спектральные составляющие с частотами
![]()
![]() (5)
(5)
где m и n – в общем случае любые положительные числа. Такого рода спектр носит название комбинационного.
Таким изменением спектра в радиотехнике пользуются для измерения степени отклонения данной системы от линейности. На вход системы подается колебание P(t); изучается спектр получаемого на выходе колебания ![]() . Комбинационные частоты
. Комбинационные частоты ![]()
![]() не возникают в том единственном случае, когда система линейна.
не возникают в том единственном случае, когда система линейна.
На основании этого можно утверждать, что при динамическом нагружении КЭ-модели балки-стенки, имеющей трещину, гармонически изменяющейся во времени силой, на спектре должны появиться комбинационные частоты, кратные частоте вынужденных колебаний.
На рис. 6 приводятся примеры численного моделирования динамического процесса балки–стенки при различной длине трещины, при нагружении одной гармонической силой ![]() , приложенной в 25 узле. При этом число учитываемых собственных частот и форм колебаний принималось равным 5. Шаг интегрирования принимался равным 0,5е-4 сек, так как при большем шаге не хватало итераций (ограничение равно 200). Наблюдение велось на интервале от 0 до 0,5 сек (10000 шагов). Частотный диапазон при расчете спектра виброперемещений 21-го узла принимался равным от1 до 5000 рад/сек. При этом можно определять как вибропараметры КЭ-модели, так и виброусилия, возникающие на Gap-элементах, что позволяет расcчитать напряженно-деформированное состояние в районе трещины в процессе динамического деформирования конструкции.
, приложенной в 25 узле. При этом число учитываемых собственных частот и форм колебаний принималось равным 5. Шаг интегрирования принимался равным 0,5е-4 сек, так как при большем шаге не хватало итераций (ограничение равно 200). Наблюдение велось на интервале от 0 до 0,5 сек (10000 шагов). Частотный диапазон при расчете спектра виброперемещений 21-го узла принимался равным от1 до 5000 рад/сек. При этом можно определять как вибропараметры КЭ-модели, так и виброусилия, возникающие на Gap-элементах, что позволяет расcчитать напряженно-деформированное состояние в районе трещины в процессе динамического деформирования конструкции.
|
|
|
|
|
|
|
|
|
|
На рис. 6 видно, как изменяется отклик 21-го узла КЭ-модели и его спектр в зависимости от длины трещины. На этом рисунке слева показаны деформированные состояния на различных временных шагах и при различной длине, которые показывают, что при движении балки-стенки вверх трещина раскрывается, а при движении вниз трещина закрывается и берега трещины не "наползают" друг на друга, что объясняется работой Gap-элементов. В особенности это хорошо наблюдается студентами при анимации динамического деформирования балки-стенки.
Решение нелинейного матричного уравнения (3) приводит к появлению в отклике гармоник, кратных основной частоте, амплитуды которых возрастают по мере увеличения длины трещины, что подтверждает правильность высказанного выше утверждения. На рис. 6 из спектров, приведенных справа, видно, как появляются гармоники, кратные основной частоте, в момент зарождения трещины, и амплитуды этих гармоник растут с ростом длины трещины.
В средней части рис. 6 показаны фрагменты виброперемещений 21-го узла, из сравнения которых видно, как изменяется колебание рассматриваемого узла в зависимости от длины трещины. При движении КЭ-модели на закрытие трещины на полупериодах колебаний на основной частоте наблюдаются колебания на собственной частоте, возникающие в результате соударения берегов трещины, которые быстро затухают. При движении КЭ-модели на раскрытие трещины на полупериодах колебаний на основной частоте собственные колебания отсутствуют, что подтверждает правильность моделирования физического процесса. На спектрах это явление отражается в виде "всплеска" на гармониках в области собственной частоты.
На рис. 7 по результатам проведенного численного эксперимента построены графики изменения амплитуд основной и четных гармоник, а также первой собственной частоты в зависимости от длины трещины.
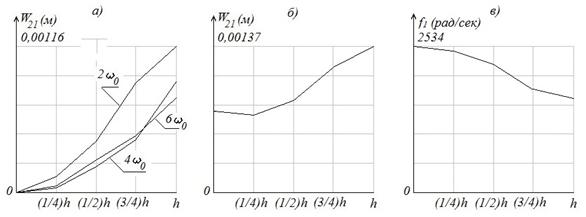
Рис. 7. Изменение основных характеристик вибрационного процесса в зависимости от глубины трещины: а – амплитуд колебаний на четных гармониках; б – амплитуд колебаний на основной частоте; в – первой собственной частоты КЭ-модели.
Особый интерес представляет бигармоническое воздействие на КЭ-модель. В работе [5] рассматривается бигармоническое воздействие на нелинейный элемент с квадратичной характеристикой, где показывается, что помимо высших гармоник возникают также комбинационные частоты, причем порядок комбинационных частот N равен двум. В работе[1] отмечается важная закономерность: "слагаемые со степенью N в характеристике нелинейного элемента обуславливает появление комбинационных составляющих с предельным порядком, равным степени этого слагаемого".
В нашем случае таким нелинейным элементом, преобразующим спектр входного сигнала, является КЭ-модель, имеющая трещину, но степень характеристики этого нелинейного элемента неизвестна. Причем нелинейность КЭ-модели зависит от длины трещины, что является очевидным фактом. Имеется возможность построить степенную характеристику нелинейного элемента (нелинейной КЭ-модели) по результатам численного расчета.
Рис. 8 демонстрирует, как изменяется спектр при бигармоническом воздействии ![]() на нелинейную КЭ-модель в зависимости от длины трещины. Анализ этих спектров показывает, что в сложном колебательном процессе присутствуют комбинационные частоты первого порядка (ω1, ω2), второго порядка (2ω1, 2ω2, ω1+ω2, ω1–ω2), третьего порядка (3ω1, 3ω2, 2ω1+ω2, 2ω1–ω2, 2ω2+ω1, 2ω2–ω1) и более высоких порядков. Наличие комбинационных компонент говорит о том, что в нелинейной КЭ-модели происходит взаимодействие колебаний, соответствующих отдельным компонентам входного воздействия. На рис. 8 также видно (в особенности при длине трещины l, близкой к высоте сечения), что наиболее представительными параметрами возникновения и развития трещины являются амплитуды на комбинационных частотах, кратных сумме основных частот.
на нелинейную КЭ-модель в зависимости от длины трещины. Анализ этих спектров показывает, что в сложном колебательном процессе присутствуют комбинационные частоты первого порядка (ω1, ω2), второго порядка (2ω1, 2ω2, ω1+ω2, ω1–ω2), третьего порядка (3ω1, 3ω2, 2ω1+ω2, 2ω1–ω2, 2ω2+ω1, 2ω2–ω1) и более высоких порядков. Наличие комбинационных компонент говорит о том, что в нелинейной КЭ-модели происходит взаимодействие колебаний, соответствующих отдельным компонентам входного воздействия. На рис. 8 также видно (в особенности при длине трещины l, близкой к высоте сечения), что наиболее представительными параметрами возникновения и развития трещины являются амплитуды на комбинационных частотах, кратных сумме основных частот.
Фрагменты колебательных процессов 21-го узла показаны на рис. 9,а в зависимости от длины трещины l. На рис. 9,б представлены графики изменения амплитуд на основных и комбинационных частотах, кратных сумме основных, также в зависимости от длины трещины.
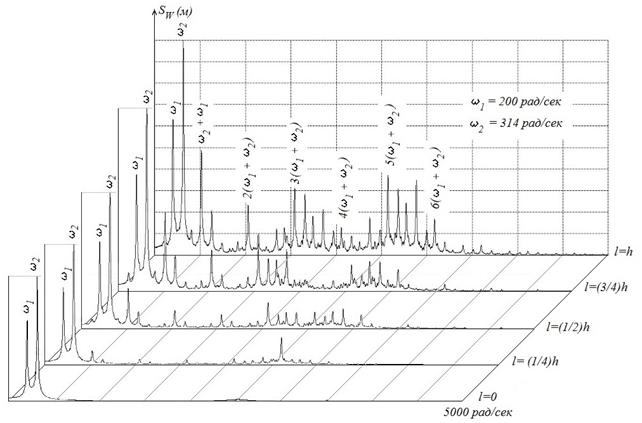
Рис. 8. Изменение спектра виброперемещений 21-го узла при увеличении длины трещины l
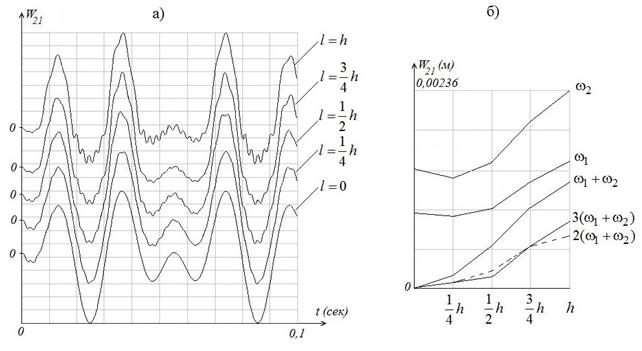
Рис. 9. Изменение в зависимости от глубины трещины: а – виброперемещений 21-го узла;
б – амплитуд колебаний на основных и комбинационных частотах
Полученные в результате численного эксперимента вибропараметры позволяют судить о возникновении и глубине дефекта в виде трещины при проведении мониторинга конструкции в процессе ее эксплуатации.
Таким образом, в процессе динамического анализа студенты отрабатывают методику численного определения двух диагностических признаков:
-
наличия трещины (появление в спектре комбинационных частот на частотах возмущения);
-
длины трещины (по высоте пиков в спектре на комбинационных частотах).
Ценность конечно-элементного подхода в преподавании дисциплины "Основы вибродиагностики конструкций и машин" состоит в следующем:
-
осуществляется адаптация студентов к профессиональным пакетам, применяемым на предприятиях;
-
дорогостоящий натурный эксперимент заменяется численным (компьютерным) экспериментом;
-
на экране студент в реальности видит динамический процесс деформации объекта во времени, что в традиционном изложении курса показать практически невозможно.
Основная ценность работы состоит в том, что впервые в практике вибродиагностики при формировании КЭ-модели применяется Gap-элемент для выделения диагностических признаков возникновения и развития трещин. Проведенные выше исследования в рамках учебного процесса убедительно показывают возможность такого подхода при вибродиагностике реальных инженерных сооружений.
Рецензенты:
Ерофеев В.И., д.ф.-м.н., профессор, заместитель директора по научной работе Института проблем машиностроения РАН, г. Нижний Новгород;
Орлов Л.Н., д.т.н., профессор, заведующий кафедрой "Автомобили и тракторы", Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.




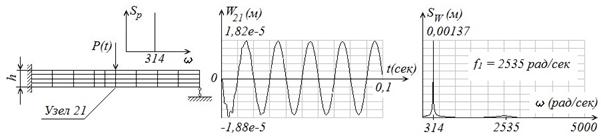
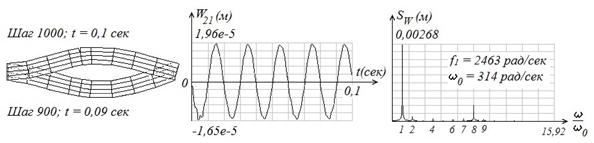
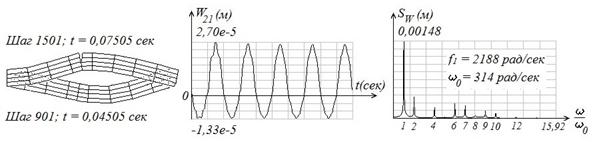
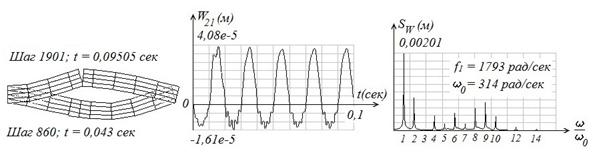
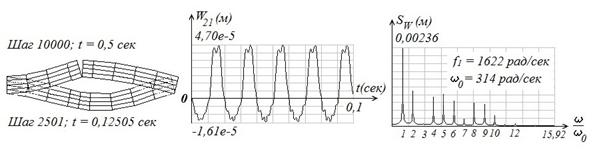 Рис. 6. Прохождение гармонического сигнала через КЭ-модели, имеющих трещину различной длины
Рис. 6. Прохождение гармонического сигнала через КЭ-модели, имеющих трещину различной длины