Интерес к задачам околоэкранной аэродинамики возник в 60-х годах прошлого века и связан с работами Р.Е. Алексеева [8]. В комплексе проблем, связанных с проектно-конструкторскими исследованиями, центральное место занимает задача о движении на произвольном отстоянии от границы крыла конечного размаха. Первые решения таких задач методом функциональных параметров получены А.Н. Панченковым [5, 7]. Позже им же создана квадрупольная теория крыла вблизи экрана [6], которая конструктивно использует малость отстояния крыла от экрана, позволяющую перейти от моделирования несущей поверхности слоем диполей к слою квадруполей, распределенных на экране под крылом. Это вырождение дает возможность перейти от сингулярного интегрального уравнения к дифференциальному соотношению в плоских потоках и к уравнению Пуассона для области течения под крылом в пространственном случае. Для задач со свободной поверхностью первые такие алгоритмы построены в [3, 4]. Обширный круг задач по рассматриваемой теме представлен также в монографии Басина М.А. и Шадрина В.П. [1]. В [10] была разработана расчётная схема, основанная на квадрупольном вырождении фундаментальных структур.
Рассмотрим задачу о движении на малой высоте над поверхностью раздела жидкостей с различной плотностью крыла конечного размаха. Пусть малоискривленное крыло ![]() движется с постоянной скоростью
движется с постоянной скоростью ![]() на малой высоте
на малой высоте ![]() над границей раздела SL двух жидкостей различных плотностей,
над границей раздела SL двух жидкостей различных плотностей, ![]() – плотность верхней жидкости,
– плотность верхней жидкости, ![]() – плотность нижней жидкости. Введем систему координат, связанную с крылом,
– плотность нижней жидкости. Введем систему координат, связанную с крылом, ![]() – проекция поверхности крыла
– проекция поверхности крыла ![]() на координатную плоскость
на координатную плоскость ![]() ,
, ![]() – проекция поверхности
– проекция поверхности ![]() на невозмущённую границу раздела жидкостей.
на невозмущённую границу раздела жидкостей.
Введём потенциал ускорений:![]() – для верхней жидкости и
– для верхней жидкости и ![]() – для нижней жидкости. Тогда исходную задачу можно сформулировать как краевую задачу для уравнения Лапласа от потенциала ускорений с соответствующими краевыми условиями:
– для нижней жидкости. Тогда исходную задачу можно сформулировать как краевую задачу для уравнения Лапласа от потенциала ускорений с соответствующими краевыми условиями:
![]() ,
, ![]() ; (1)
; (1)
![]() ,
, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ;
;
![]() ,
, ![]() ;
;
![]() ,
, ![]() .
.
Здесь ![]() ,
, ![]() – пространство, занятое жидкостью;
– пространство, занятое жидкостью;![]() ;
; ![]() ,
, ![]() ,
, ![]() – нормальная составляющая скорости точек на крыле, b – полуразмах крыла,
– нормальная составляющая скорости точек на крыле, b – полуразмах крыла, ![]() ,
, ![]() ;
; ![]() ,
, ![]() – малый действительный параметр, устремляемый к нулю в конечных результатах.
– малый действительный параметр, устремляемый к нулю в конечных результатах.
Решение краевой задачи (1) будем искать в форме интегрального оператора типа потенциала двойного слоя: ![]() . Основное двумерное сингулярное интегральное уравнение в линейной задаче о движении крыла вблизи границы раздела жидкостей имеет вид [4, 5, 6, 7]
. Основное двумерное сингулярное интегральное уравнение в линейной задаче о движении крыла вблизи границы раздела жидкостей имеет вид [4, 5, 6, 7]
![]() , (2)
, (2)
где 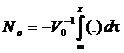 ;
;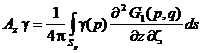 ;
; ![]() ;
; ![]() ;
;
![]() – плотность двойного слоя на поверхности
– плотность двойного слоя на поверхности ![]() ;
; ![]() – проекция на нормаль к
– проекция на нормаль к ![]() скорости набегающего потока жидкости;
скорости набегающего потока жидкости; ![]() – фундаментальное решение уравнения Лапласа, удовлетворяющее условию теории волн малой амплитуды на поверхности раздела жидкостей [2, 7, 9].
– фундаментальное решение уравнения Лапласа, удовлетворяющее условию теории волн малой амплитуды на поверхности раздела жидкостей [2, 7, 9].
![]() , (3)
, (3)
![]() ,
,
где G1, G2 – потенциалы единичного источника, движущегося в верхней жидкости для верхней (индекс 1) и для нижней (индекс 2) жидкостей, ![]() – гармонические функции (волновые интегралы), вид которых после обезразмеривания будет приведён далее,
– гармонические функции (волновые интегралы), вид которых после обезразмеривания будет приведён далее,![]() ,
, ![]() .
.
Поставленная задача будет решена, если будет найдено решение уравнение (2) с ядром (3). В [5, 7] впервые получено решение уравнения (2) методом функциональных параметров. В [3,4] близкое к (2) уравнение о движении тела по поверхности тяжелой жидкости после асимптотического анализа структур типа (3) сведено к двумерному сингулярному уравнению и уравнению Вольтерра типа свёртки с периодическим ядром по продольной координате. Получено решение первого приближения по шкале ![]() . Существенного упрощения расчетов можно добиться, используя квадрупольные вырождения фундаментальных структур (3) [6, 10].
. Существенного упрощения расчетов можно добиться, используя квадрупольные вырождения фундаментальных структур (3) [6, 10].
Поскольку (3) – гармонические функции, которые вместе со всеми своими производными равномерно непрерывны всюду в трехмерном евклидовом пространстве, исключая точки ![]() и
и ![]() , то их разложения в ряды Тейлора относительно точек
, то их разложения в ряды Тейлора относительно точек ![]() , лежащих на границе раздела, – равномерно сходящиеся ряды.
, лежащих на границе раздела, – равномерно сходящиеся ряды.
Тогда, используя асимптотическую квадрупольную теорию крыла, которая основана на аппроксимации фундаментальной структуры двумя членами ряда [3, 4, 6], получим:
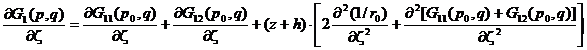 . (4)
. (4)
Этому уравнению можно придать вид
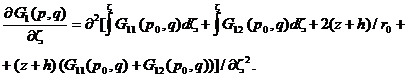 (5)
(5)
Введем безразмерные величины соотношениями:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() – число Фруда,
– число Фруда, ![]() – хорда,
– хорда, ![]() – размах,
– размах, ![]() – относительное удлинение крыла. Выделив действительную часть в выражениях для
– относительное удлинение крыла. Выделив действительную часть в выражениях для![]() в (3), получим (черточки над безразмерными координатами далее опущены):
в (3), получим (черточки над безразмерными координатами далее опущены):
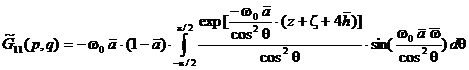 ,
,
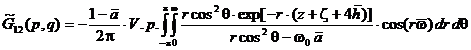 ,
,
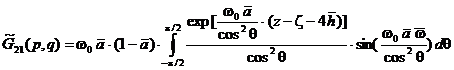 ,
,
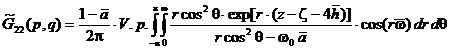 ,
,
![]() ,
, ![]() .
.
В силу гармоничности функций ![]() ,
, ![]() ,
, ![]() и использования (5) в (2), получим краевую задачу:
и использования (5) в (2), получим краевую задачу:
![]() , (6)
, (6)
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
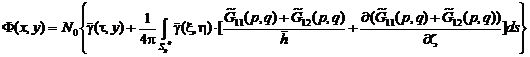 . (7)
. (7)
Уравнение Пуассона (6) описывает движение жидкости в ограниченной области между крылом и поверхностью раздела жидкостей. Исходя из аппроксимации (5), предполагается, что возмущения за пределы этой области не распространяются. Поэтому в (7) оператор ![]() следует заменить на оператор
следует заменить на оператор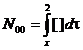 , определяющий отсутствие возмущений перед поверхностью
, определяющий отсутствие возмущений перед поверхностью ![]() . Вместо (7) можно записать
. Вместо (7) можно записать
![]() , (8)
, (8)
где 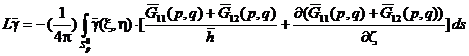 ;
; ![]() ;
; ![]() .
.
Плотность двойного слоя ![]() , определенная из уравнения (8),приводит к следующему значению потенциала скоростей
, определенная из уравнения (8),приводит к следующему значению потенциала скоростей
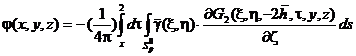 . (9)
. (9)
Форма свободной поверхности жидкости, коэффициенты подъёмной силы и волнового сопротивления определяются по известным формулам [5]:
![]() (10)
(10)
![]() , (11)
, (11)
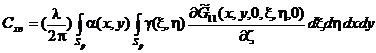 , (12)
, (12)
где ![]() – относительная высота волны в долях полухорды крыла, Сy – коэффициент подъёмной силы,
– относительная высота волны в долях полухорды крыла, Сy – коэффициент подъёмной силы,![]() – коэффициент волнового сопротивления,
– коэффициент волнового сопротивления,![]() – местный угол атаки.
– местный угол атаки.
Таким образом, аэрогидродинамические характеристики низколетящего крыла могут быть найдены в результате последовательного решения краевой задачи (6), интегрального уравнения (8) и вычисления их по формулам (9)-(12). Полученная последовательность задач (6), (8), (9) может быть решена численно по расчетной схеме, приведенной в [10].
Для примера были выполнены расчёты гидроаэродинамических характеристик крыла, близкого по параметрам к крылу судна на динамической воздушной подушке (СДВП) «Волга-2» из [8]. Характерная особенность этого СДВП – сверхмалое отстояние крыла от опорной поверхности (около 0.1 м от хвостика на скорости 30 – 35 м/с). Для такого отстояния расчёт характеристик возможен только с использованием квадрупольной теории или метода сращиваемых асимптотических разложений. Некоторые результаты расчёта, в которых крыло имеет форму плоской бестелесной поверхности, представлены на рис. 1 – рис. 5.
На рис.1 изображен график функции![]() – отношения коэффициента подъёмной силы крыла с λ=1, углом атаки α=40, относительными отстояниями
– отношения коэффициента подъёмной силы крыла с λ=1, углом атаки α=40, относительными отстояниями![]() и
и![]() , к значению того же коэффициента при движении крыла с большой скоростью в зависимости от числа Фруда, а на рис.2 – зависимость от числа Фруда коэффициента волнового сопротивления. Насколько известно авторам, влияние числа Фруда на коэффициент подъёмной силы крыла, движущегося на малой высоте над поверхностью раздела жидкостей с различными плотностями не исследовано, и факт наличия точки экстремума зависимости
, к значению того же коэффициента при движении крыла с большой скоростью в зависимости от числа Фруда, а на рис.2 – зависимость от числа Фруда коэффициента волнового сопротивления. Насколько известно авторам, влияние числа Фруда на коэффициент подъёмной силы крыла, движущегося на малой высоте над поверхностью раздела жидкостей с различными плотностями не исследовано, и факт наличия точки экстремума зависимости![]() ранее не был известен. Для объяснения этого эффекта были выполнены подробные расчёты формы свободной поверхности под крылом и коэффициента подъёмной силы в диапазоне чисел Фруда от 1.43 до 6.64 для относительных отстояний
ранее не был известен. Для объяснения этого эффекта были выполнены подробные расчёты формы свободной поверхности под крылом и коэффициента подъёмной силы в диапазоне чисел Фруда от 1.43 до 6.64 для относительных отстояний![]() и
и![]() . На рис.3, 4, 5 представлен рельеф свободной поверхности (волновые системы) для чисел Фруда 1.43, 2.48 и 4.04, соответственно. При числе Фруда 1.43 волновая система имеет характерный для корабельных волн в закритической (
. На рис.3, 4, 5 представлен рельеф свободной поверхности (волновые системы) для чисел Фруда 1.43, 2.48 и 4.04, соответственно. При числе Фруда 1.43 волновая система имеет характерный для корабельных волн в закритической (![]() ) области вид. Для числа Фруда 4.04 форма волновой поверхности типична для рельефа под крылом экраноплана – валики за боковыми кромками крыла и незначительная впадина под несущей поверхностью. Точка экстремума коэффициента подъёмной силы (
) области вид. Для числа Фруда 4.04 форма волновой поверхности типична для рельефа под крылом экраноплана – валики за боковыми кромками крыла и незначительная впадина под несущей поверхностью. Точка экстремума коэффициента подъёмной силы (![]() ) соответствует фазе перехода волновых систем из первого типа во второй, причём волновая поверхность под крылом заметно возвышается над невозмущённым уровнем. Следует особо отметить, что для исследованной формы крыла (плоская бестелесная поверхность) относительное отстояние не влияет на положение точки экстремума коэффициента подъёмной силы. Коэффициент волнового сопротивления низколетящего крыла ведёт себя, как и положено в теории корабельных волн – с ростом числа Фруда монотонно стремится к нулю, так как для исследуемых систем интерес представляют закритические скорости.
) соответствует фазе перехода волновых систем из первого типа во второй, причём волновая поверхность под крылом заметно возвышается над невозмущённым уровнем. Следует особо отметить, что для исследованной формы крыла (плоская бестелесная поверхность) относительное отстояние не влияет на положение точки экстремума коэффициента подъёмной силы. Коэффициент волнового сопротивления низколетящего крыла ведёт себя, как и положено в теории корабельных волн – с ростом числа Фруда монотонно стремится к нулю, так как для исследуемых систем интерес представляют закритические скорости.
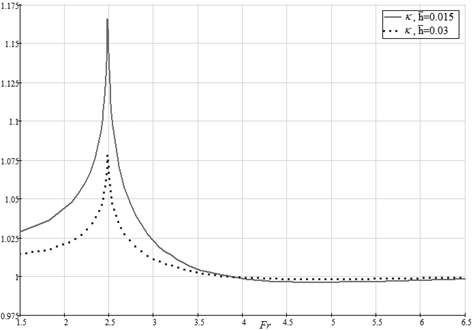
Рис. 1. Зависимость функции![]() от числа Фруда
от числа Фруда
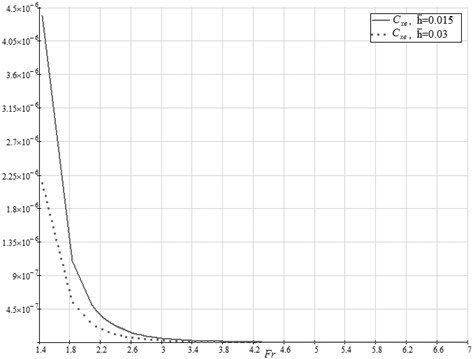
Рис. 2. Зависимость коэффициента волнового сопротивления от числа Фруда
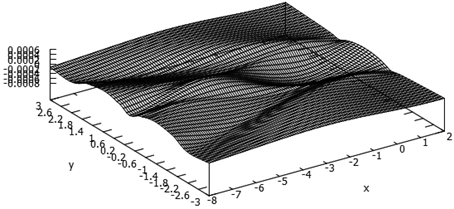
Рис. 3. Рельеф свободной поверхности жидкости под низколетящим крылом, ![]()
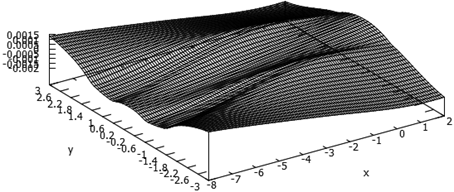
Рис. 4. Рельеф свободной поверхности жидкости под низколетящим крылом, ![]()
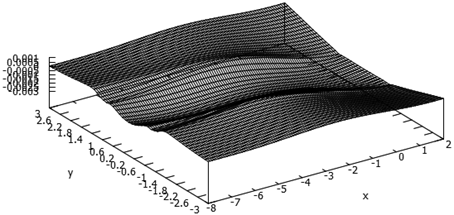
Рис. 5. Рельеф свободной поверхности жидкости под низколетящим крылом, ![]()
Таким образом, квадрупольное вырождение фундаментальных структур оказывается эффективным в задачах о движении несущей поверхности на малой высоте над поверхностью раздела жидкостей с различными плотностями. Выполненные расчёты выявили особенности влияния числа Фруда на аэродинамические характеристики низколетящего крыла.
Рецензенты:
Панченков А.Н., д.т.н., профессор, профессор кафедры Аэро-гидродинамики, прочности машин и сопротивления материалов государственного ОУИнститут Транспортных Систем Нижегородского государственного технического университета имени Р.Е. Алексеева, г. Нижний Новгород;
Катаева Л.Ю., д.ф.-м.н., профессор, профессор кафедры Прикладная математика Нижегородского филиала МИИТ (государственное ОУ), г.Нижний Новгород.



