При динамическом и импульсном воздействии в сооружении распространяются волны напряжений. Волны напряжений образуют области возмущений. Материал находится в напряженно-деформированном состоянии. В зависимости от скорости воздействия области возмущений могут быть локальными или занимать все тело. Локальное возмущение имеет место при сильном динамическом (импульсном) воздействии. Возмущение, занимающее все тело, происходит при слабом динамическом (статическом) воздействии. При импульсном (волновом) воздействии существуют локализованные напряжения и деформации, способствующие возникновению разрушения в одной части тела независимо оттого, что происходит в другой его части. При интерференции волн напряжений их интенсивности складываются. Они могут достигать значений, превосходящих предел прочности материала. В этом случае наступает разрушение материала. Напряженное состояние импульсного (волнового) нагруженного тела может изменяться так быстро, что возникающие деформации и разрушения еще не успевают распространиться, как распределение напряжений изменится, так как скорости распространения волн напряжений достигают 
, а нарушение прочности (трещины) распространяются со скоростью не более 
. В настоящее время активно применяются численные методы для решения различных задач нестационарной механики деформируемого твердого тела. Однако, при решении сложных задач возникают проблемы оценки достоверности полученных результатов. В работах [1, 3– 4, 9–10] приведена информация о постановке волновых задах теории упругости.
Для решения задачи о моделировании упругих взрывных волн в деформируемых областях сложной формы рассмотрим некоторое тело Г в прямоугольной декартовой системе координат ХОУ, которому в начальный момент времени 
сообщается механическое воздействие. Предположим, что тело Г изготовлено из однородного изотропного материала, подчиняющегося упругому закону Гука при малых упругих деформациях.
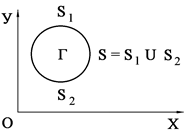
Рис. 1. Некоторое тело Г в прямоугольной декартовой системе координат XOY
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
, 
, 
,
, 
,
,
, 
, 
, 
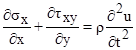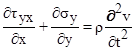, (1)
где: 
, 
и 
– компоненты тензора упругих напряжений; 
, 
и 
– компоненты тензора упругих деформаций; 
и 
– cоставляющие вектора упругих перемещений вдоль осей 
и 
соответственно; 
– плотность материала;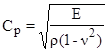 
– скорость продольной упругой волны; 
– скорость поперечной упругой волны; 
– коэффициент Пуассона; 
– модуль упругости; 
– граничный контур тела 
.
Систему (1) в области, занимаемой телом Г, следует интегрировать при начальных и граничных условиях.
Начальные условия в области Г зададим в виде
,
, 
, 
, 
, (2)
где: 
, 
, 
и 
– заданные в области Г функции.
Граничные условия зададим в виде:
составляющих компонентов тензора упругих напряжений на границе 
, 
, 
; (3)
составляющих компонентов вектора упругих перемещений на границе 
, 
, 
, (4)
где: 
и 
– направляющие косинусы; 
,
,
и 
– заданные на границе 
функции.
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями – используем метод конечных элементов в перемещениях. Задача решается методом сквозного счета, без выделения разрывов. Чтобы выполнить динамический расчет методом конечных элементов, нужно иметь матрицу жесткости и матрицу инерции конечного элемента.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела 
, записываем приближенное значение уравнения движения в теории упругости
, 
, 
, (5)
где: 
– матрица инерции; 
– матрица жесткости; 
– вектор узловых упругих перемещений; 
– вектор узловых упругих скоростей перемещений; 
– вектор узловых упругих ускорений; 
– вектор узловых упругих внешних сил.
Соотношение (5) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями. Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями привели к линейной задаче Коши (5). В работах [1, 3–10] приведена информация о численном моделировании нестационарных волн напряжений в деформируемых телах. Рассмотрим интегрирование системы линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями.
Для интегрирования уравнения (5) конечноэлементным вариантом метода Галеркина приведем его к следующему виду
, 
. (6)
Интегрируя по временной координате соотношение (6) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
, 
.
(7)
где: 
– шаг по временной координате.
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина. Рассмотрим устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках. Система уравнений (5) для внутренних и граничных узловых точек, полученная в результате интегрирования уравнения движения теории упругости, должна давать решение, сходящееся к решению исходной системы (1).
Шаг по временной переменной 
определяем из следующего соотношения
, (8)
где: 
– длина стороны конечного элемента.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках. На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных динамических воздействиях на сооружения. При разработке комплекса программ использовался алгоритмический язык Фортран-90. Некоторые вопросы в области постановки, разработки методики, алгоритма и результатах решенных нестационарных динамических задач рассмотрены в работах [1–10]. Рассмотрим задачу об интерференции плоских продольных упругих волн напряжений в виде треугольного импульса.
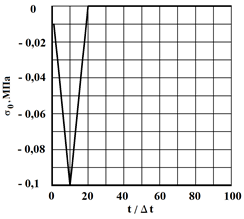
Рис. 2. Воздействие в виде треугольного импульса
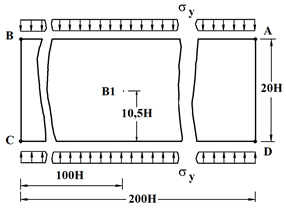
Рис. 3. Постановка задачи об интерференции волн напряжений
На границе пластинки 
(рис. 3) приложено нормальное напряжение 
(рис. 2), которое при 
изменяется линейно от 
до 
, а при 
от до (
, 
= – 0,1 МПа (–1 кгс/см2)). На границе пластинки 
(рис. 3) приложено нормальное напряжение , которое при 
изменяется линейно от до , а при 
от до (, 
= 0,1 МПа (1 кгс/см2)). Граничные условия для контуров 
и 
при 
. Отраженные волны от контуров и не доходят до исследуемых точек при 
. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных. Для примера на рис. 4 представлено изменение нормального напряжения 
(
) во времени 
в точках 
. Сравнение с результатами других методов показало хорошее совпадение, что позволяет сделать вывод о физической и математической достоверности результатов численного решения динамических задач, полученных методом конечных элементов в перемещениях.
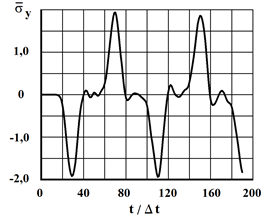
Рис. 4. Изменение нормального напряжения во времени в точке
Достоверность численного метода приведена в следующих работах [1, 3–7, 9–10]. Методика, алгоритм, комплекс программ и результаты решенных задач рекомендуются для использования в научно-технических организациях, специализирующихся в области динамического расчета технических объектов.
Рецензенты:
Савчин В.М., д.ф.-м.н., профессор, профессор кафедры Математического анализа и теории функций факультета Физико-математических и естественных наук Российского университета дружбы народов, г.Москва.
Зволинский В.П., д.х.н., профессор, профессор кафедры Экологического мониторинга и прогнозирования Экологического факультета Российского университета дружбы народов, г.Москва.