Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение. Коэффициент тангенциального сопротивления является характеристикой трения текстильных материалов (КТС). Трение текстильных материалов играет важную роль в технологии швейного производства и оказывает существенное влияние на технологические и эксплуатационные характеристики тканей. От трения зависят условия выполнения и параметры технологических операций по изготовлению швейных изделий, таких как настилание, разрезание и стачивание материалов, выбор конструкций швов, методов обработки открытых срезов и др. Трение влияет и на назначение материала [1]. На сегодняшний день не существует стандартных методов определения КТС полотен. В связи с этим и изыскание возможности прогнозирования КТС текстильных полотен при конфекционировании материалов для одежды актуально.

Цель исследования. Поиск возможности прогнозирования КТС текстильных полотен при конфекционировании материалов для одежды.

Методы исследования: эксперимент по разработанной авторами методике, регрессионный анализ полученных данных, проверка адекватности и работоспособности полученной модели.

Результаты исследования и их обсуждение. Для исследования были выбраны полульняные ткани (табл. 1).

Таблица 1

Характеристики строения и свойств льняных тканей

Все ткани выработаны в лаборатории кафедры ткачества КГТУ на станке АТ-100-5М с зевообразовательной кареткой РК-12. В качестве основы использована хлопчатобумажная пряжа То = 25текс х2 текс, а в утке льняная пряжа Ту =56 текс. Ткани выработаны полотняным, сатиновым и мелкоузорчатыми переплетениями с раппортом шесть по основе и утку. В работе ставилась задача изучить влияние переплетения льняных тканей на КТС.

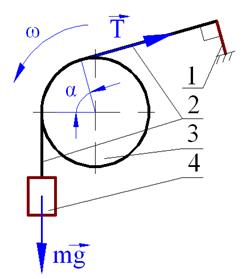
Рис. 1. Схема устройства для определения КТС:

1- тензорезисторный датчик
2- верхняя проба
3- барабан
4- груз

Определение коэффициентов тангенциального сопротивления текстильных полотен проводилось по разработанному в КГТУ и запатентованному методу [2,3], так как стандартные методы определения КТС текстильных полотен отсутствуют. На рис.1 представлена схема устройства и векторы распределения сил, возникающих при контакте взаимодействующих поверхностей проб исследуемых полотен. Пробы имеют прямоугольную форму. Одну пробу (110х350 мм) закрепляют на поверхности вращающегося с постоянной угловой скоростью ω барабана 3. Вторая проба 2 (50х500 мм), огибая цилиндрическую поверхность и охватывая её под углом, равным α, свисает под действием груза 4 массой m. Второй конец пробы 2 прикрепляется к консольному силоизмерительному тензорезисторному датчику 1. [3]. Величину КТС определяют по известной формуле Эйлера [3,4].

Испытания проводились при скорости относительного перемещения тканей 6 мм/с и углом взаимного охвата полотен 30º. Полученные экспериментальные данные по силе трения и КТС льнохлопковых полотен представлены в табл. 1. Наибольшее значение КТС (f=0.83) характерно для тканей полотняного переплетения, что объясняется минимальной длинной перекрытий. Для тканей сатинового переплетения КТС минимальный (f=0.63). Ткани сатинового переплетения благодаря гладкой поверхности устойчивы к трению, хорошо скользят и поэтому применяются в качестве подкладки [1]. Также прослеживается тенденция уменьшения КТС при увеличении длины перекрытий.

Анализ взаимосвязи КТС и характеристик переплетения тканей: коэффициентов связности нитей в переплетении, коэффициентов подвижности нитей в переплетении и коэффициент переплетения [1,4,5], показал наличие тесной взаимосвязи КТС и коэффициентов переплетения Fn [5] по Н.С. Ерёминой (рис. 2).

Методом наименьших квадратов найдена зависимость КТС от коэффициента переплетения. Полученная регрессионная модель представляет собой степенную функцию (1).

Был проведен анализ регрессионной модели, который подтвердил ее адекватность. Для проверки адекватности модели использовался критерий Фишера. Результаты исследований приведены в табл. 2.

Графическое отображение зависимости представлено на рис. 2, где также приведены значения КТС для каждого вида тканей.

Таблица 2

Анализ результатов регрессии

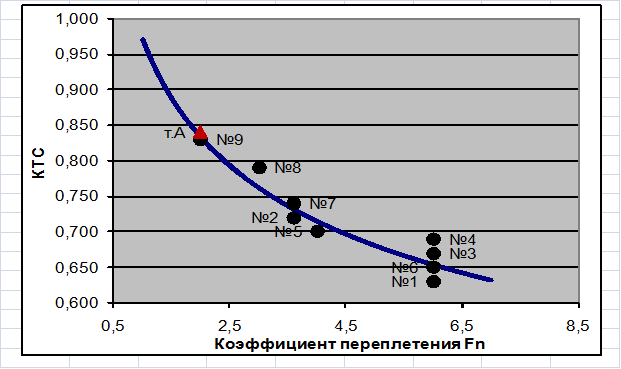
Рис. 2 Зависимость КТС льняных тканей от коэффициентов переплетения

Данная математическая модель была апробирована для льняной ткани с известными характеристиками строения (Fn=2) (табл.3)

Таблица 3

Характеристики строения и свойств льняной ткани для проверки работоспособности модели

Экспериментальное значение КТС для чисто льняной пробы f=0.84 (точка А на рис.2) отличается на 1.2 % от полученного расчетным способом значения КТС f(2)=0.83 по регрессионной модели (1).

Таким образом, можно сделать вывод о работоспособности полученной модели. Кроме того, полученный результат позволяет утверждать, что модель применима не только для льнохлопковых, но и для чистольняных тканей. Модель позволяет рассчитать величину КТС по коэффициенту переплетения ткани. Кроме того, полученная модель появляется реализовать возможность проектирования льняных тканей с заданными значениями тангенциального сопротивления, варьируя их характеристиками строения.

Выводы

1. Новым методом получены экспериментальные справочные данные по коэффициентам тангенциального сопротивления льнохлопковых тканей.

2. Установлена зависимость коэффициента тангенциального сопротивления от коэффициента переплетения для льняных тканей.

3. Предложенная математическая модель позволяет прогнозировать коэффициент тангенциального сопротивления льняных тканей при конфекционировании материалов по переплетению и проектировать льняные ткани с заданными свойства.

Рецензенты:

Жуков В.И., д.т.н., профессор, заведующий кафедрой «Механических технологий волокнистых материалов», ФГБОУ ВПО «Костромской государственный технологический университет», г. Кострома.

Проталинский С.Е., д.т.н., профессор кафедры «Теории механизмов и машин, ДМ и ПТМ»,

ФГБОУ ВПО «Костромской государственный технологический университет», г. Кострома.