Проблема обучения решению физических задач стоит как перед преподавателями школ, так и высших учебных заведений.
Умение решать задачи - это один из критериев усвоения знаний. В теории обучения физике процесс решения задач рассматривается как средство обучения и воспитания. Ему как методу обучения, должны быть присущи все основные функции: побуждающая, познавательная, воспитывающая, развивающая и контролирующая [1].
В работе А.В. Усовой [1] отмечается, что процесс решения физических задач осуществляется в четыре действия: 1- осознание, восприятие задачи; 2- планирование процесса решения; 3- осуществление процесса решения; 4- проверка полученного результата решения - раскрывается смысл этих действий и приводится обобщенная структура процесса решения задач при обучении физике. С другой стороны, условие любой физической задачи, которая предлагается студенту, есть модель, с той или иной степенью точности отражающая реальный физический процесс. Как известно [2] модель создается для получения информации о реальном явлении или процессе, необходимой для решения определенной задачи. Компьютерная техника позволяет визуализировать и исследовать свойства таких моделей непосредственно при проведении семинарских и практических занятий. Концепции использования возможностей информационно-образовательной среды (ИОС) (компьютерных технологий) для повышения эффективности обучения физике изложены в работе [3].
В Кузбасской государственной педагогической академии обучение решению задач по физике с применением ПК на физико-математическом и технолого-экономическом факультетах проводили по следующей технологии: Первые 3-4 занятия обучающимся предлагались простые, тренировочные модели (задачи). Цели этих занятий: усвоить основные законы изучаемого раздела, приобрести умение анализировать модель и находить способы определения параметров, характеризующих данную модель и связь между ними, научиться строить модель на компьютере. Схему проведения первых занятий условно можно обозначить таким образом (рис.1):
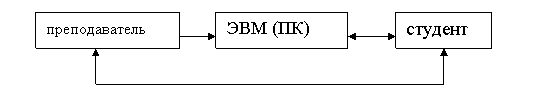
Построение простых, тренировочных моделей на первых занятиях со студентами проводится с помощью преподавателя. Кроме того, одновременно рассматриваются типы моделей, методы построения и визуализации моделей [8].
В дальнейшем, по мере овладения программным обеспечением и методами построения моделей, студенты получают более сложные задания, и схема занятий изменяется (рис.2).

В качестве среды для моделирования на ПК использовался пакет MathCad, как наиболее удобный для проведения занятий такого типа [4-7]. В таблице1 приведены этапы традиционной методики решения физических задач [1] и при использовании ПК.
Таблица 1. Этапы традиционной методики решения физических задач и при использовании ПК.
| Традиционная методика [1] | Использования ПК |
| Условия задачи | модель |
| I. Осознание, восприятие задачи II. Планирование решения. III. Осуществление процесса решения. IV. Проверка полученного результата | I. Анализ модели, ее восприятие. II. Анализ параметров, характеризующих модель и установление их взаимосвязей. III. Построение математической модели. IV. Выбор среды, в которой строится данная модель на ПК. V. Проектирование и отладка компьютерной модели. VI. Исследование модели. VII. Нахождение значений параметров модели определяемых требованием задачи. VIII. Проверка результатов. |
Таким образом, методика проведения традиционных, практических и семинарских занятий является неотъемлемой частью компьютерной технологии обучения решению физических задач. Преимущество компьютерной технологии перед традиционной методикой решения физических задач по нашему мнению заключается в следующем:
1. Занятия становятся более интересными для студентов;
2. Задачи, предлагаемые студентам, носят исследовательский характер, что позволяет более глубоко изучить рассматриваемый процесс или явление;
3. Возможность индивидуальной работы с каждым студентом;
4. Непосредственная реализация межпредметных связей – физика-математика-информатика, а в зависимости от рассматриваемой модели возможно и с другими предметами.
5. Возможность визуализации изучаемой модели и изучения процесса в динамике.
Рассмотрим следующий пример:
модель.
Фарфоровый шар радиусом R=10 см заряжен равномерно с объемной плотностью ρ=15 нКл/м3. Диэлектрическая про ницаемость фарфора ε=5.
Требования задачи
Определить значения напряженности в точках:
1) на расстоянии r1=5 см от центра шара; 2)на поверхности шара; 3) на расстоянии r2=15 см от центра шара.
Анализ модели и выявление связей между параметрами, характеризующими модель
Для построения модели воспользуемся теоремой Гаусса
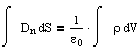
1. Определим связь между параметрами для случая r1 < R
![]()
![]()
![]()
![]()
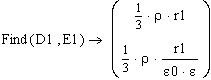 - напряженность электрического поля внутри шара.
- напряженность электрического поля внутри шара.
2) Определим связь между параметрами для случая ![]()
![]()
![]()
![]()
![]()
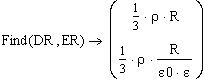 - напряженность электрического поля на поверхности шара
- напряженность электрического поля на поверхности шара
3) Определим связь между параметрами для случая ![]()
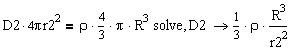
![]()
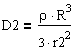
![]()
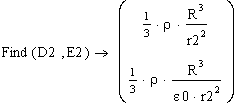 - напряженность электрического поля в пространстве окружающем шар.
- напряженность электрического поля в пространстве окружающем шар.
Проектирование и отладка компьютерной модели
На листовом поле среды MathCad вводим исходные данные и уравнения, связывающие параметры системы между собой.
![]()
![]()
![]()
![]()
![]()
![]()
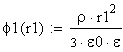
![]()
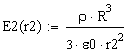
![]()
 .
.
а) б)
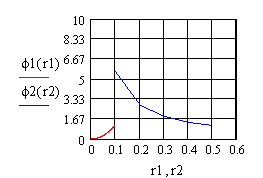
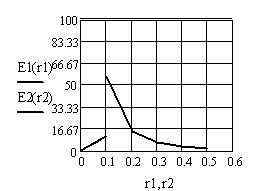
Рисунок 1. а). Зависимость напряженности электрического поля E(r); б). Зависимость потенциала электрического поля φ (r).
Из графиков видно, что на границе раздела сред с различными ε наблюдается скачок на пряженности и потенциала электрического поля, что соответствует известным литературным данным.
Построение трехмерной модели поля.
Для изображения трехмерной модели поля построим фигуру вращения (см. предыдущие графики) вокруг оси Z.
Для r<R 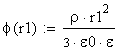
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для r>R ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
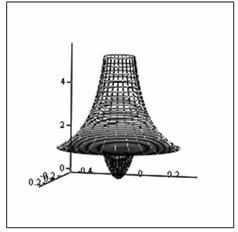
 .
.
![]()
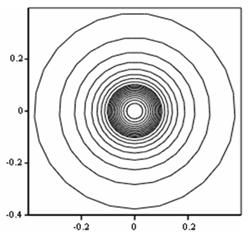
![]() .
.
а) б)
Рисунок 2. а). Поверхностный график электрического поля заряженного шара б). Линии равного потенциала.
Выполняем требования задачи.
Находим значения напряженности электростатического поля в интересующих нас точках пространства.
![]()
![]()
![]()
![]()
Меняя значения параметров можно исследовать построенную модель и наблюдать за из менениями поля.
Для более успешного проведения занятий такого типа, особенно на второй стадии (схема 2), когда студенты освоили методологию компьютерного моделирования, необходимо создать возможность использования студентами во время занятия учебной и справочной литерату рой, т.е. предоставить им больше самостоятельности.
СПИСОК ЛИТЕРАТУРЫ
1. А.В.Усова, Н.Н.Тулькибаева. Практикум по решению физических задач. М.: «Просвещение», 2001 г., с. 206.
2. С.В.Борисенок. Современный подход к моделированию в курсе теоретической физики в педагогических университетах //Физическое образование в вузах. -2004г.- т.10.- №3.- с. 6-18.
3. А.И.Назаров, С.Д.Ханин. Информационно-образовательная среда как средство повышения эффективности обучения физике в вузе//Физическое образование в вузах.-2004г.- т.10.- №3.- с. 45-60.
4. В.Г.Суппес. Использование ЭВМ при изучении гармонических колебаний //Физическое образование в вузах.-2001 г.-т.7.-№3.-.81-91.
5. В.Г.Суппес. Решение задач по механики в среде MathCad.//Физическое образование в вузах.-2002 г., т.8., №4, с.143-149.
6. В.Г.Суппес. Физическое моделирование при изучении электростатических полей в курсе общей физики. //Современные наукоемкие технологии. - 2004 г.-№4.-.54.
7. М.Д.Старостенков, В.Г.Суппес. Использование среды MathCad при решении задач в курсе общей физики. //Успехи современного естествознания. -2004 г.-№8.-с.96.
8. Е.Бенькович, Ю.Колесов, Ю.Сениченков. Практическое моделирование динамических систем.



