Введение
Последние два десятилетия ситуацию в молочной промышленности существенно ухудшилась [4]. Тем не менее, в нескольких регионах России отмечается значительный прогресс и стабилизация ситуации в отрасли. Во Владимирской области наблюдается существенный рост количества сельскохозяйственных и животноводческих хозяйств. Впервые за последние годы поголовье крупного рогатого скота в хозяйствах всех категорий увеличилось на 0,8%, коров – на 1,5%. Производство мяса увеличилось к уровню 2005 года на 14,2%, молока - на 2,9% и составило в 2010 году 63,7 тыс. тонн и 311,9 тыс. тонн соответственно [1].
Анализ современных направлений исследований автоматизации животноводческих предприятий
Одной из наиболее важных задач в условиях ведения животноводства является эффективная селекция животных предприятия и сохранения качества генофонда на высшем уровне. Как показывает статистика сельскохозяйственного департамента Владимирской области, в результате неэффективной селекционной работы увеличивается падеж скота в раннем возрасте, уменьшается уровень среднего надоя за лактационный период, ухудшается иммунная защита животных, следствием чего становится высокая степень риска заболевания вирусными инфекциями, наиболее опасными из которых является лейкоз крупного рогатого скота.
Исследования в данной области начали проводиться с середины 50-ых годов и продолжаются до настоящего времени. Отдельно стоит отметить современную работу [3] американских ученых из университета штата Висконсин. Используя математическую статистику для анализа данных о животных, искусственно разбитых на 28 групп по среднему ежегодному показателю надоя, авторы разрабатывают новую методику отбора животных, основанную на процентном соотношении наследуемых признаков и их генетической корреляции. В работе [9] авторы пользуются средствами аппроксимации данных о молочных надоях для определения концентрации протеина и белка для каждого животного. Используя средства математической статистики, корреляционного анализа, математического моделирования и методы аппроксимации в статье приводятся математические выкладки и графические материалы на их основе, позволяющие оценить уровень надоев, содержание протеина и белка в молоке в зависимости от времени года. В работе [10] авторы используют Байесовский анализ для оценки наследуемости и генетической корреляции между молочными надоями, интервалами между отелами и длинной лактации. Математический анализ и средства математической статистики по отношению к различным параметрам жизнедеятельности животных молочного предприятия применяются также в работах [5-8]. Стоит отметить также работы отечественных авторов. В работе [2] авторы проводят экономический анализ состояния финансового стимулирования для увеличения молочной продуктивности одного животного и приходят к выводу, что при определённых условиях всевозрастающие затраты на молокоотдачу становятся больше, чем сам эффект от продажи продукта. В работе авторы путем статистического анализа находят оптимальной значение надоя для одного животного, дальнейшее увеличение которого не будет приносить предприятию дополнительного дохода.
Исследование закона распределения производственных данных
При разработке интеллектуального продукта автоматизации животноводческого производства требуется решать проблемы индивидуального прогнозирования состояния и качества продукции для каждой конкретной особи на предприятии. Необходимо отслеживать отклонения и резкие колебания в величине показателей надоев молока, ежедневной активности, изменения температуры, химического состава молока и др. показателей. С этой целью необходимо провести анализ реальных данных, состоящий из следующих этапов:
- Визуальный анализ данных. Общая характеристика временного ряда исследуемых показателей.
- Разделение временного ряда показателя на периоды, в которых присутствуют и отсутствуют отклонения значений, требующих внимание к особи.
- Определение законов, которым подчинены данные этих периодов.
- Построение математической модели и разработка информационно-аналитической системы на ее основе.
На рис. 1 представлен временной ряд удоя животного за один лактационный период. В рамках решения задачи индивидуального прогнозирования надоев животных на подобных диаграммах выделяются стабильные участки (A-B, C-D). На графике видны резкие нехарактерные перепады значений (B-C, D-E), что говорит о внеплановом снижении объема производства молока и проблемах в состоянии животного. Подобные ситуации необходимо отслеживать на ранних стадиях их возникновения.
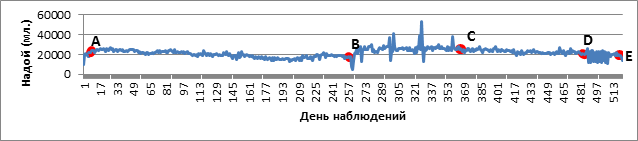
Рис. 1. – график изменения значения ежедневного надоя
Поскольку численность поголовья крупного рогатого скота (КРС) на крупных предприятиях исчисляется тысячами голов отслеживать подобные изменения для каждого животного человеком весьма проблематично. В этом случае возможен человеческий фактор возникновения ошибок, что, в конечном итоге, приведет либо к гибели животных, либо к ухудшению качества выпускаемой продукции. В связи с этим возникает актуальная задача автоматизации выявления нестабильностей удоев в период лактации.
На стабильном участке график ряда значений удоев можно разложить на две составляющих: тренд и отклонение от тренда. Тренд характеризует основную тенденцию изменения надоев во времени. Взаимодействие между собой регулярных составляющих может быть представлено как аддитивная комбинация:
![]() , (1)
, (1)
где Y(t) – значение надоя в момент t;
T(t) – тренд изменения надоев;
E(t) – отклонение от тренда.
Для разработки математической модели поиска нестабильных участков, которые могут свидетельствовать о критических изменениях здоровья животного, необходимо знать закон распределения значений E(t) на стабильных и нестабильных участках. В данной статье ставится задача определения вида этого закона.
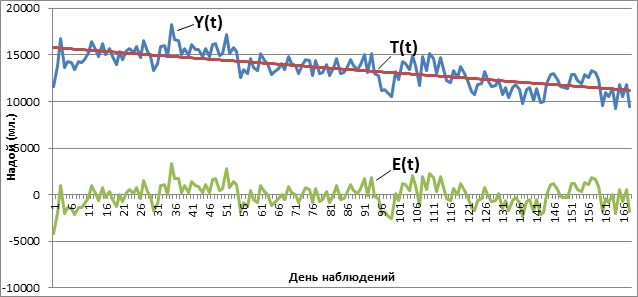
Рис. 2. – Y(t) - График изменения ежедневных надоев на стабильном участке; T(t) – трендовая линия аппроксимации Y(t); E(t) – График отклонения ежедневных надоев от тренда
Используя метод наименьших квадратов, построили трендовую линию изменения надоев T(t). Функция E(t) находится из формулы (1). Построим гистограмму значений эмпирического распределения функции E(t), разделенных на 17 периодов (рис 3).
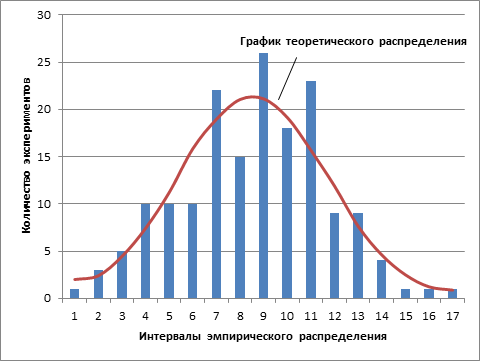
Рис. 3. – Эмпирическое распределение экспериментальных данных отклонения от тренда
На рисунке 3 визуально наблюдаем подобие эмпирического распределения нормальному закону распределения случайных величин. Это предположение не является фактом, поэтому выдвинем его в качестве гипотезы H0.
Доказательство гипотезы подчинения производственных данных нормальному закону распределения
Для проверки этой гипотезы используем критерий согласия Пирсона χ2. Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины. Для экспериментального ряда, включающего от 100 до 200 наблюдений, рекомендуют выбирать количество интервалов от 15 до 20. Количество экспериментальных отчетов, в нашем случае, составляет 168, поэтому возьмём 17 интервалов. Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20% от их общего количества, допускаются интервалы с частотой nj ≥ 2. Оценка χ2 вычисляется по формуле:
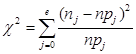 , (2)
, (2)
где pj - вероятность попадания изучаемой случайной величины в j-й интервал, вычисляемая в соответствии с теоретическим законом распределения. При вычислении вероятности pj нужно иметь в виду, что левая граница первого интервала и правая последнего должны совпадать с границами области возможных значений случайной величины. При нормальном распределении первый интервал изменяется до -∞, а последний - до +∞.
Нулевую гипотезу о соответствии выборочного распределения теоретическому закону проверяют путем сравнения вычисленной по формуле (2) величины с критическим значением χ2α, найденным по таблице критических точек распределения Пирсона для уровня значимости α и числа степеней свободы k = e1 - m - 1. Здесь e1 - число интервалов после объединения; m - число параметров, оцениваемых по рассматриваемой выборке (для нормального распределения m = 2). Если выполняется неравенство:
χ2 ≤ χ2α , (3)
то нулевую гипотезу не отвергают. При несоблюдении указанного неравенства принимают альтернативную гипотезу о принадлежности выборки неизвестному распределению.
Таким образом, принимаем предположение о подчинении данных о надоях (рис. 3) нормальному распределению за гипотезу H0,требующую доказательства. Проверяя гипотезу с помощью критерия согласия χ2примем уровень значимости α = 0,05.
Результаты расчетов приведены в таблице 1.
Таблица 1 – Расчет значения критерия согласия Пирсона χ2
|
Отчеты эмпирического распределения |
Пределы эмпирического распределения |
Пределы теоретического распределения |
Значение функции Лапласа на границах интервала Φ(zj) |
Оценка вероятности попадания в интервалpj |
|
||||
|
Исходное |
С объединением |
Левый предел |
Правый предел |
Левый предел |
Правый предел |
Левый предел |
Правый предел |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
9 |
-4172 |
-2660 |
-∞ |
-2,26 |
0,000 |
0,012 |
0,053
|
0,003
|
|
3 |
-2660 |
-2282 |
-2,26 |
-1,94 |
0,012 |
0,026 |
|||
|
5 |
-2282 |
-1903 |
-1,94 |
-1,62 |
0,026 |
0,053 |
|||
|
10 |
10 |
-1903 |
-1525 |
-1,62 |
-1,30 |
0,053 |
0,097 |
0,044 |
0,895 |
|
10 |
10 |
-1525 |
-1147 |
-1,30 |
-0,98 |
0,097 |
0,164 |
0,067 |
0,131 |
|
10 |
10 |
-1147 |
-769 |
-0,98 |
-0,65 |
0,164 |
0,258 |
0,094 |
2,156 |
|
22 |
22 |
-769 |
-391 |
-0,65 |
-0,33 |
0,258 |
0,371 |
0,113 |
0,488 |
|
15 |
15 |
-391 |
-13 |
-0,33 |
-0,01 |
0,371 |
0,496 |
0,125 |
1,740 |
|
26 |
26 |
-13 |
365 |
-0,01 |
0,31 |
0,496 |
0,622 |
0,126 |
1,128 |
|
18 |
18 |
365 |
743 |
0,31 |
0,63 |
0,622 |
0,736 |
0,114 |
0,068 |
|
23 |
23 |
743 |
1121 |
0,63 |
0,95 |
0,736 |
0,829 |
0,093 |
3,426 |
|
9 |
9 |
1121 |
1499 |
0,95 |
1,28 |
0,829 |
0,900 |
0,071 |
0,704 |
|
9 |
9 |
1499 |
1877 |
1,28 |
1,60 |
0,900 |
0,945 |
0,045 |
0,242 |
|
4 |
7 |
1877 |
2255 |
1,60 |
1,92 |
0,945 |
0,973 |
0,055 |
0,529 |
|
1 |
2255 |
2633 |
1,92 |
2,24 |
0,973 |
0,987 |
|||
|
1 |
2633 |
3011 |
2,24 |
2,56 |
0,987 |
0,995 |
|||
|
1 |
3011 |
3389 |
2,56 |
+∞ |
0,995 |
1,000 |
|||
|
Всего n = 168 |
|
|
|
|
∑ = 1 |
|
χ2 = 11,506 |
||
Изначально исходные данные о надоях были предварительно обработаны: рассчитаны параметры линейной функцииY(t). Разность данных о наблюдениях и значений функции тренда в точках наблюдения позволила получить ряд значений функции E(t). Отсчеты этой функции с помощью операции квантования разбиты на промежутки (столбец 1, таблица 2), и получены соответствующие границы интервалов (столбец 3, 4, таблица 2) и количество вхождений наблюдений в эти интервалы (столбец 2 Исходное). В 5-ом, 6-ом столбцах показаны результаты вычисления границ интервалов, выраженные через нормированную случайную величину:
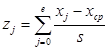 , (4)
, (4)
где xср и s – выборочное среднее значение и среднее квадратическое отклонение выборочных данных, соответственно. Значения этих оценок были найдены для исходных данных наблюдений заранее и представлены в таблице 2.
Таблица 2 – Основные статистические параметры, необходимые для вычисления значения критерия согласия Пирсона χ2
|
Минимальное значение отклонения от тренда надоев |
-4171,80729 |
|
Максимальное значение отклонения от тренда надоев |
3389,225627 |
|
Среднеквадратическое отклонение линии отклонения от тренда надоев |
1175,355677 |
|
Среднее значение отклонений от тренда надоев |
-0,00096104 |
Находим значения функции Лапласа для границ интервалов и заносим их в 7-ой, 8-ой столбцы. Оценка вероятности попадания значений в интервалы (10-ый столбец) представляет собой разность значений функции Лапласа на правой и левой границе интервала. Если интервалы объединяются, вычисляют разность значений функции на границах объединенного интервала. Сумма значений pj, в столбце 6 всегда будет равна единице. В 7-ой столбец заносят оценки математических ожиданий числа наблюдений по интервалам, которые определяем умножением оценки вероятности pj на общее число образцов в выборке n =100.
Результаты
Таким образом, рассчитаем значение χ2 по формуле, используя значения 9, 10 столбцы при уровне значимости α = 0.05 и количестве степеней свободы k = 11 – 2, где 2 – число параметров функции нормального распределения.
После расчетов значение величины χ2 = 11,5060317.
При e = 12 и α = 0,05 для доказательства заявленной гипотезы о подчинении исходных данных нормальному закону распределения необходимо исходя из таблицы значений χ2[2], чтобы полученное значение было меньше 16,9.
Таким образом, неравенство:
χ2 ≤ 16,9
верно, а следовательно верно и утверждение:
χ2 ≤ χ2α
Что позволяет сделать вывод о доказательстве выдвинутой в начале исследований гипотезы.
Заключение
Доказательство факта подчинения числового ряда наблюдаемых значений нормальному закону распределения позволяет разработать математическую модель отслеживания случайных всплесков значений. На практике внеплановые всплески представляют собой резкие отклонения наблюдаемых значений от нормы, что в условиях реального производства может означать резкое ухудшение здоровья животных, качества выпускаемой продукции, и, как следствие этого, финансовые потери. На основе проведенного исследования и подобных исследований других важных параметров животных был разработан метод отслеживания случайных всплесков в значениях различных параметров. Данный метод лежит в основе алгоритма мониторинга отклонений значений характеристик производственного процесса и состояния животных. Разработанный алгоритм реализован в системе в рамках интеллектуального программного модуля контроля производственного процесса.
Рецензенты:
Жизняков А.Л., д.т.н., профессор, зав. кафедрой САПР МИ (ф), г. Муром.
Андрианов Д.Е., д.т.н., доцент, зав. кафедрой ИС МИ (ф), г. Муром.



