Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Логинов В.Н. 1 Космынин А.В. 1 Широкова З.В. 1 Медведовская Ю.А. 1

---

1 Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Комсомольский-на-Амуре государственный технический университет»

Рассмотрено аналитическое решение задачи определения эксплуатационных характеристик частично пористого цилиндрического подшипника с внешним наддувом газа, работающего в гибридном режиме (при вращающемся вале). В основе методики лежит модифицированное уравнение Рейнольдса, решение которого представляется в виде суммы двух решений. Первое – соответствует решению статической задачи определения поля давления (без вращения вала). Второе решение находится с помощью метода разложения по малому параметру, в качестве которого используется число сжимаемости. В результате решения задачи определяется несущая способность подшипника, жесткость его смазочного слоя, угол положения нагрузки. Сравнение теоретических результатов расчета с опытными данными характеристик различных частично пористых газовых подшипников показало не вполне удовлетворительную точность.

Статья в формате PDF

165 KB

жесткость смазочного слоя

несущая способность

газовая смазка

газовый подшипник

пористая среда

1. Высокоскоростной шпиндельный узел внутришлифовального станка для прецизионной обработки деталей летательных аппаратов / А. В. Космынин, В. С. Щетинин, А. С. Хвостиков, А. В. Смирнов, С. С. Блинков // Фундаментальные исследования. – 2011. – Ч.1, № 8. – С. 137-138.

2. Константинеску В. Н. Газовая смазка. – М.: Машиностроение, 1968. – 718 с.

3. Космынин А. В., Чернобай С. П., Виноградов С. В. Расчет частично пористых газовых подшипников высокоскоростных шпиндельных узлов // Автоматизация и современные технологии. – 2008. – № 10. – С. 8-12.

4. Космынин А. В., Шаломов В. И. Аэростатические шпиндельные опоры с частично пористой стенкой вкладыша // Современные проблемы науки и образования. – 2006. – № 2. – С.69-70.

5. Космынин А. В., Щетинин В. С. Расчет несущей способности газомагнитных опор высокоскоростных шпиндельных узлов // СТИН. – 2010. – № 9. – С. 6-8.

6. Космынин А. В., Щетинин В. С. Эксплуатационные показатели высокоскоростных шпиндельных узлов металлообрабатывающего оборудования с газомагнитными опорами // Успехи современного естествознания. – 2009. – № 11. – C. 69-70.

7. Космынин А. В., Щетинин В. С., Иванова Н. А. Методика расчета несущей способности газомагнитного подшипника высокоскоростного шпиндельного узла // Вестник Самарского ГТУ. – 2010. – №4. – C. 226-229.

8. Логинов В. Н., Космынин А. В., Широкова З. В. Аналитическое решение задачи определения характеристик цилиндрического газового подшипника // Современные проблемы науки и образования. – 2012. – № 5; URL: http//www.science-education.ru/105-7188 (дата обращения: 18.10.2012).

9. О результатах экспериментальной проверки расчётных характеристик высокоскоростных шпиндельных узлов металлорежущих станков с частично пористыми газостатическими опорами / А. В. Космынин, В. И. Шаломов, И. Г. Суходоев, С. В. Виноградов // Фундаментальные исследования. – 2009. – №1. – С. 32-33.

10. Щетинин В. С., Космынин А. В. Математическая модель расчета несущей способности высокоскоростного шпиндельного узла на газомагнитной опоре // Трение и смазка в машинах и механизмах. – 2010. – № 8. – С. 31-35.

Настоящая работа является продолжением работы [8], в которой была изложена аналитическая методика расчета эксплуатационных характеристик частично пористых газостатических подшипников. Ниже рассмотрена аналитическая методика расчета характеристик таких опор при вращающемся вале, т.е. при работе опор в гибридном режиме.

Гибридный режим работы бесконтактных подшипников с внешним наддувом газа характеризуется наличием дополнительной подъемной силы, возникающей в результате вращения ротора. Механизм ее образования заключается в том, что при вращении эксцентрично расположенного во вкладыше вала газ под действием касательных сил вязкости увлекается его поверхностью и вгоняется в клиновидный зазор между валом и вкладышем. Такое явление называют эффектом самогенерации давления или эффектом смазочного клина [1]. С учетом внешнего наддува это приводит к дополнительному сжатию газа в смазочном слое и такому распределению давления, в результате которого несущая способность подшипника увеличивается. Гибридный режим работы подшипников называют также комбинированным.

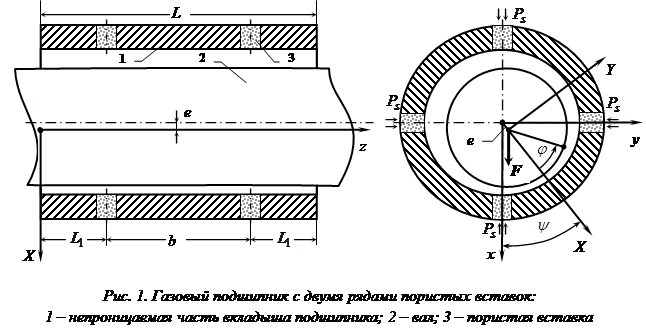
Вращение вала, в отличие от случая работы опор в режиме подвеса, приводит к асимметричному распределению давления газа в зазоре [4, 5, 7, 10]. Вследствие этого, вал смещается от равновесного положения в направление своего вращения и образует отличный от нуля угол ориентации нагрузки (рис. 1). Следует отметить, что малый угол ориентации нагрузки считается целесообразным с точки зрения устойчивой работы опоры [3].

При работе газовых опор в гибридном режиме дифференциальное уравнение для поля давления принимает вид или в безразмерных координатах

, (1)

где , , – угловая скорость вращения вала, – относительное давление, – среднее давление в зазоре подшипника, полученное при решении статической задачи () [8], – относительная толщина смазочного слоя, – число сжимаемости. Решение этого уравнения будем искать в виде , где – решение статической задачи (), – газодинамическая составляющая давления.

При подстановке в уравнение (1) получаем

.

В последнем уравнении сумма первого и пятого слагаемых тождественно равна нулю. В оставшихся слагаемых, в первом приближении, заменим давление средним значением , в результате получаем уравнение .

Первый интеграл этого уравнения имеет вид

, (2)

здесь и далее штрих – производная по . Это обыкновенное дифференциальное уравнение, которое в квадратурах не интегрируется. Будем решать его методом малого параметра, в качестве которого можно принять относительный эксцентриситет или число сжимаемости. Тестирующие расчеты показали, что в достаточно широком изменении режимных и конструктивных параметров опоры, более адекватно экспериментальным данным отвечают расчеты, в которых малым параметром является число сжимаемости .

Разложим относительное давление в ряд по степеням : , . Постоянная интегрирования в уравнении (2) также зависит от , поэтому ее тоже раскладываем в ряд: . Подставляя эти разложения в уравнение (2), получаем

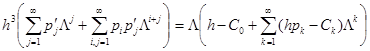. (3)

Приравнивая коэффициенты при одинаковых степенях , получаем бесконечную систему линейных обыкновенных дифференциальных уравнений. При интегрировании этих уравнений, будут появляться интегралы вида , которые можно выразить через интегралы

.

Для последних интегралов легко получить рекуррентную формулу. Действительно, дифференцируя по параметру , находим или

. (4)

Первый интеграл вычисляется непосредственно:

.

Если ввести обозначения: , , то

, где .

Дифференцируя необходимое число раз и используя рекуррентную формулу (4), последовательно находим:

, , ;

,
, , ;

,
, , , ;

,
, , , , ;

,
, , , , .

При этом .

При интегрировании уравнений системы (3) будут появляться постоянные интегрирования, значения которых определяются следующим образом. Из условия отсутствия перетекания смазки в направлении оси () получаем равенство [2] 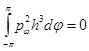, откуда находим:

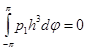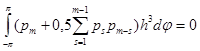; , (5)

Приравнивая коэффициенты при первой степени , из системы (3) получаем уравнение , решение которого имеет вид

, (6)

где – постоянная интегрирования. Из первого равенства системы (5) получаем 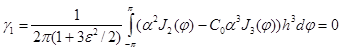, так как функции нечетные, а функция – четная. Постоянная находится из условия непрерывности функции : , .

Подставляя постоянную интегрирования в равенство (6) и приводя подобные слагаемые, получаем решение первого приближения

, (7)

где .

При из системы (3) получаем второе уравнение или, с использованием равенства , , откуда

,

где .

Из условия непрерывности функции получаем , а из второго равенства системы (5) (:

, ,

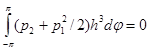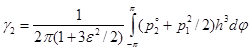где . Таким образом, второе решение имеет вид

. (8)

При из системы (3) находим , откуда:

,

. (9)

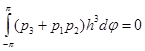Здесь, в силу нечетности функций и функции ( – нечетная, – четная), из третьего равенства системы (5) (: , получаем . Постоянная находится из условия непрерывности функции и вычисляется по формуле

.

По аналогичной схеме находится давление . Формула, по которой вычисляется , в виду ее громоздкости, не приводится. Следует отметить, что является четной функцией и представляет собою линейную комбинацию обратных степеней со второй по шестую.

В результате, используя формулы (7) – (9), получаем приближенное решение уравнения (3) с точностью .

С целью проверки адекватности математической модели было проведено сравнение с опытными данными, полученными на экспериментальных стендах [6, 9] ФГБОУ ВПО «КнАГТУ». На рис. 2 представлены результаты расчетов и экспериментальные данные для двухрядного подшипника, имеющего следующие геометрические размеры: длина подшипника L = 60 мм, диаметр подшипника D = 50 мм; средний радиальный зазор с = 45 мкм, диаметр пористых вставок = 6,3 мм; раздвижка линий наддува b = 30 мм, высота вставок = 7,5 мм. В одном ряду наддува располагалось 6 вставок. В качестве пористых вставок использовалась модифицированная древесина березы с коэффициентом проницаемости = 4,23∙10-12 м2.

Для представления характеристик подшипника в зависимости от безразмерного комплекса прямо пропорционального среднему радиальному зазору, в рассмотрение введен конструктивный параметр , который был равен = 0,266.

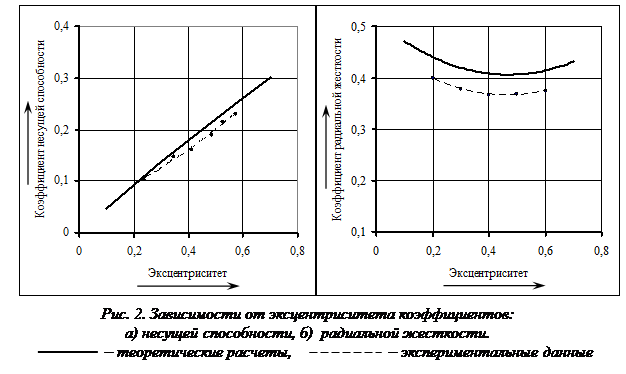
Испытания подшипника выполнены при относительном давлении наддува и числе сжимаемости , равном .

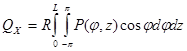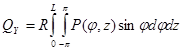
Основные интегральные характеристики вычислялись по формулам: – несущая способность, , – коэффициент несущей способности, – коэффициент радиальной жесткости смазочного слоя.

Из представленных графиков видна хорошая согласованность теоретических и опытных данных. Максимальная относительная погрешность при вычислении , не превосходит 10 %.

Рецензенты:

Олейников А. И., д.ф.-м.н., профессор, зав. кафедрой «Механика и анализ конструкций и процессов» ФГБОУ ВПО «Комсомольский-на-Амуре государственный технический университет», г. Комсомольск-на-Амуре.

Биленко С. В., д.т.н., доцент, зав. кафедрой «Технология машиностроения» ФГБОУ ВПО «Комсомольский-на-Амуре государственный технический университет», г. Комсомольск-на-Амуре.

Библиографическая ссылка