Введение
Определение состояния костного регенерата в месте повреждения конечности является актуальной проблемой ортопедии, решение которой позволило бы проводить более точную диагностику состояния восстанавливаемой конечности, костного регенерата, что в свою очередь привело бы к сокращению послеоперационного периода и уменьшило количество послеоперационных осложнений. В разное время несколько групп исследователей пытались решить эту проблему, однако точность их методов не позволяла достоверно оценивать состояние костного регенерата из-за несовершенства применяемых ими методик и приборов [1–3, 6]. Поэтому в лечебных учреждениях до сих пор используется рентгеновский метод контроля, при котором периодически производятся рентгеновские исследования места повреждения, и уже на их основе врач принимает решение о снятии или не снятии аппарата Илизарова. Основным недостатком этого метода является недостаточная эффективность рентгенографии для определения состояния костного регенерата. В результате трактовка снимков сильно зависит от опыта врача-ортопеда, что выливается в достаточную субъективность данного метода. Поэтому часто аппарат Илизарова снимается позже, чем надо. Также бывают случаи раннего снятия аппарата Илизарова, когда поврежденная конечность еще не срослась. Все это приводит к осложнениям у пациентов, увеличению пребывания пациентов в стационарах, что в итоге выливается в финансовые издержки медицинских учреждений.
Цель исследования – разработка физико-математической модели зоны стыка костных отломков, зафиксированных с помощью аппарата Илизарова, и вывод аналитической формулы для осевой жесткости костного регенерата.
Материал и методы
Для рассмотрения картины, происходящей со спицей аппарата Илизарова при нагрузке, воспользуемся допущением, что спица является тонким стержнем, на который, кроме поперечной нагрузки, действует продольная растягивающая сила (спица аппарата Илизарова имеет начальное натяжение).
Система «спицы – кольцо – костный регенерат» изображена на рисунке 1.
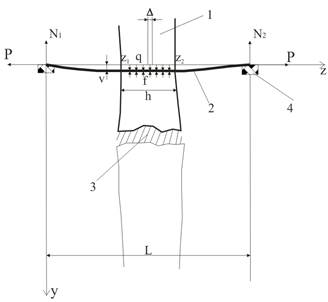
Рисунок 1. Система «спица – кольцо – костный регенерат»
1 – костные отломки; 2 – спица; 3 – костный регенерат; 4 – кольцо
На этом рисунке показан прогиб спицы v под действием распределенной нагрузки q со стороны костного отломка. На спицу также действует распределенная сила сопротивления костного регенерата f, однако на начальной стадии процесса излечения костный регенерат не оказывает значительного сопротивления, поэтому мы пока будем считать, что она равна нулю. Также на рисунке показаны силы натяжения спицы P и силы реакции опор N1 и N2. Расстояние между опорными точками на кольце равно – L, h – ширина кости (опорной площадки на спице), h = z2 - z1. Учитывая не соблюдение полной симметрии при наложении аппарата, в модель также введена величина Δ – смещение центра костного отломка (центра опорного участка спицы), относительно геометрического центра расстояния между опорными точками на кольце.
Для определения формулы величины прогиба v воспользуемся уравнением изгиба из курса сопротивления материалов [4], принимая во внимание, что спица испытывает продольно-поперечный изгиб под действием распределенной нагрузки. Это уравнение имеет следующий вид:
![]() (1)
(1)
В данном уравнении Mx*(z) – момент поперечной нагрузки в сечении с координатой z, ![]() , где P – поперечная нагрузка, E – модуль Юнга, Jx – момент инерции спицы относительно главной центральной оси Х:
, где P – поперечная нагрузка, E – модуль Юнга, Jx – момент инерции спицы относительно главной центральной оси Х:
![]()
где d – диаметр спицы.
Решение уравнения (1) имеет следующий вид:
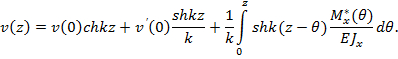
Исходя из рисунка 1 и учитывая, что f = 0, видно, что на спицу действуют сосредоточенные силы N1, N2 и распределенная нагрузка q. Поэтому интеграл в формуле выше решается с учетом следующих формул для момента поперечной нагрузки:
Mx*(z) = q[φ2(z - z1) - φ2(z - z2)] для распределенной нагрузки q, действующей на участке от z1 до z2;
Mx*(z) = Qφ1(z - b) для любой сосредоточенной силы Q в сечении z = b.
В этих формулах ![]() . Также φn(z) = 0 при z ≤ 0.
. Также φn(z) = 0 при z ≤ 0.
В итоге, опуская математические расчеты (они есть в курсе сопротивления материалов), получаем решение уравнения (1) в следующем виде:
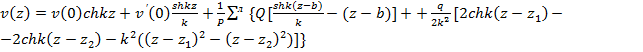 (2)
(2)
Буква л над знаком суммы означает, что суммирование распространяется только на те силы, которые приложены слева от рассматриваемого сечения.
Для участка z2 ≤ z ≤ L существует сосредоточенная сила – реакция опоры N1 в сечении z = 0 и распределенная нагрузка q на участке от z1 до z2. Учитывая также, что прогиб спицы на кольце отсутствует (v(0) = v(L) = 0), решение (2) принимает вид:
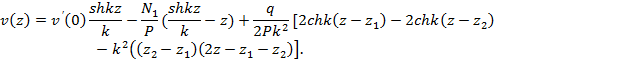
Учитывая, что z2 - z1 = h получим:
![]()
v'(0) находится из условия v(L) = 0, в итоге прогиб спицы на участке z2 ≤ z ≤ L равен:
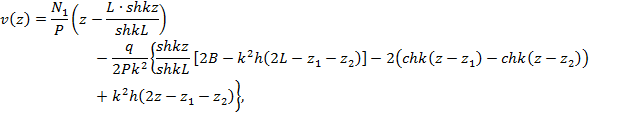
где B = ch k(L - z1) - ch k(L - z2).
Реакцию опоры N1 можно найти, используя тот факт, что сумма моментов действующих сил на спицу равно нулю, т.к. система находится в равновесии. Сумма моментов сил относительно точки приложения реакции опоры N2 (z = L, рисунок 1) выражается следующим уравнением:
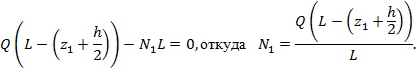
Учитывая, что Q = qh, получим:
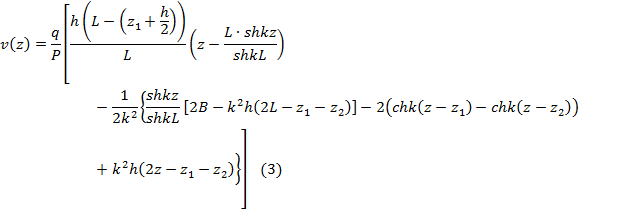
Данная модель является достаточно точной применительно к расчетам величины прогиба спицы в процессе лечения поврежденной конечности, она отражает основные тенденции изменения величины прогиба с течением времени, как будет показано ниже. Также необходимо отметить, что в ней изначально заложены некоторые индивидуальные характеристики, такие как масса пациента (от нее зависит удельная нагрузка q) и ширина костного участка, опирающегося на спицу.
Используя рассчитанную выше модель, можно аналитически показать, что с увеличением времени излечения прогиб спицы будет уменьшаться. Для этого зададимся сразу условием, что с течением времени костный регенерат увеличивает свою жесткость по неизвестному нам закону. Необходимо аналитически показать, что напряжение с тензометрических датчиков силы, установленных в стержнях аппарата Илизарова, будет уменьшаться.
Для этого зададимся некоторым фиксированным сечением zфикс = const, которое будет удовлетворять условию z2 ≤ z ≤ L. Тогда в уравнении (3) часть, стоящая в больших квадратных скобках, превратиться в некую константу, и мы можем переписать это уравнение для фиксированного сечения zфикс:
![]()
где A и есть та самая константа.
Если учитывать сопротивление костного регенерата, тогда формула (4) преобразуется в следующую формулу:
![]()
где f – распределенная сила сопротивления со стороны костного регенерата.
Делая допущение, что распределенные нагрузки на выбранную (в данном случае первую) спицу со стороны силы тяжести пациента и со стороны силы сопротивления костного регенерата распределены более-менее равномерно, получим:
![]()
![]()
где Q1 – доля силы тяжести пациента, действующая на первую спицу, Fсопр1 – доля силы сопротивления костного регенерата, действующая на первую спицу, h1 – длина первой спицы в костном отломке. Так как мы ведем расчет для периода излечения, во время которого костный регенерат является упругим, то силу сопротивления можно выразить законом Гука как:
![]()
где c1 – доля общей жесткости костного регенерата на сжатие, х1 – деформация костного регенерата. Другими словами, общая сила сопротивления в случае двух спиц выражается следующим образом:
![]()
где c – жесткость костного регенерата на сжатие, х – итоговая деформация костного регенерата в случае двух спиц.
Таким образом, формула (5) приобретет следующий вид:
![]()
В данной формуле, по сути дела, записаны две физические величины одной природы – это прогиб спицы на фиксированном участке и деформация регенерата на этом участке. В самом деле, исходя из построенной выше модели и цепочки наших рассуждений, прогиб спицы на конкретном участке должен быть равен деформации регенерата на этом участке, т.е. vфикс1 = x1. Тогда формула (6) преобразуется к виду:
![]()
Изолируя прогиб спицы в левой части и учитывая, что жесткость костного регенерата является функцией времени, получим:
![]()
![]()
Принимая во внимание то, что жесткость костного регенерата со временем увеличивается, из формулы (7) очевидно, что величина прогиба спицы будет уменьшаться со временем.
Аналогичные расчеты можно произвести и для второй спицы аппарата Илизарова. При этом прогибы спиц у краев костного отломка и в нем самом (например, в сечении zфикс = z2 для первой спицы) будут одинаковы.
Общая нагрузка на спицы аппарата Илизарова является весом пациента, т.е.:
Q = Q1 + Q2 = mg,
где m – масса пациента, g – ускорение свободного падения. Тогда можно записать:
qh1 + qh2 = mg, откуда
![]()
Таким образом, значение Q1 из формул (7) и (8) может быть рассчитано по следующей формуле:
![]()
где h1 и h2 – длины участков первой и второй спиц в костном отломке.
Аналогичным образом распределяется общая сила сопротивления костного регенерата по спицам аппарата Илизарова. Другими словами, используя формулу (8):
![]()
Как было сказано выше, прогибы спиц в костном отломке будут одинаковы, т.к. он является твердым телом, т.е. v1 = v2 = v. Поэтому общую силу сопротивления и жесткость регенерата можно представить следующими формулами:
![]()
![]()
Используя данную модель, можно установить примерную зависимость изменения напряжения с датчика силы, установленного в опорном стержне аппарата Илизарова, в зависимости от времени излечения, а также зависимость жесткости костного регенерата от напряжения с датчика.
Так как при опоре на аппарат Илизарова сила тяжести пациента полностью компенсируется реактивными силами опоры со стороны стержней аппарата Илизарова и костного регенерата, справедливо следующее выражение:
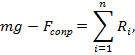
где Ri – силы реакции опоры со стороны стержней, n – количество стержней, Fсопр – общая сила сопротивления со стороны костного регенерата. Для упрощения дальнейших рассуждений будем считать, что кольцо действует на стержни аппарата более-менее равномерно, без сильных перекосов (это справедливо при правильном наложении аппарата Илизарова). Тогда можно записать, что:
![]()
![]()
Учитывая, что возникающие нагрузки на стержень будут находиться в зоне линейности тензодатчика (рабочий режим) [5], можно заключить, что напряжение с него будет пропорционально действующей на него силе:
![]()
где U – напряжение с тензодатчика (датчика силы), α – коэффициент пропорциональности, n – количество стержней. Т.к. прогиб спицы со временем уменьшается, то и напряжение с тензодатчика будет уменьшаться со временем.
Для получения формулы жесткости костного регенерата необходимо выразить прогиб спицы из (11):
![]()
Подставляя это выражение в (10), получим:
![]()
Следует отметить, что в общем случае спицы аппарата Илизарова на пациенте будут опираться на кольцо на некотором расстоянии от опорных стержней (рисунок 2.4). В результате этого нагрузка на стержни аппарата будет неодинаковой, т.е. R1 ≠ R2 ≠ R3 ≠ R4. Для детального расчета нагрузки на каждый стержень требуется модификация разработанной математической модели.
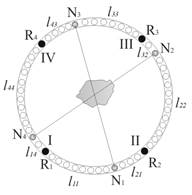
Рисунок 2. Размещение спиц относительно стержней в общем случае
На рисунке 2 показано, что контактные площадки спиц (обозначены серым цветом) в общем случае опираются на некотором расстоянии l от ближайшего опорного стержня. Для расчета такой системы введены следующие обозначения: Ni – сила, с которой спица действует на кольцо, направлена от наблюдателя; Ri – сила реакции опоры со стороны i-го стержня, направлена к наблюдателю; lij – длина дуги от i-го стержня до j-й контактной площадки спицы с кольцом. Также обозначим dij как кратчайшую длину дуги между стержнями i и j, например, d12 = l11 + l21. Так как система находится в равновесии, то сумма действующих моментов сил на спицы равна нулю. Запишем уравнения моментов относительно стержней, считая силы, направленные от наблюдателя, отрицательными, а к наблюдателю положительными:
I: ![]()
II: ![]()
III: ![]()
Уравнение сил: Q = R1 + R2 + R3 + R4.
Продолжая математические преобразования, получим следующую систему:
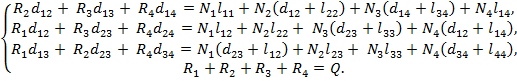
Данная система содержит 4 уравнения и 4 неизвестных: R1, R2, R3, R4, т.е. является разрешимой. Значения сил Ni могут быть найдены при отдельном рассмотрении каждой спицы с учетом закона сохранения моментов сил, как это было сделано для силы N1 в процессе построения физико-математической модели.
Выводы: полученные данные делают возможным аналитический расчет текущей осевой жесткости костного регенерата, не проникая напрямую в зону стыка костных отломков. Это открывает новые возможности в оптимизации сроков лечения пациентов, перенесших операции по чрескостному остеосинтезу.
Рецензенты:
Шеин Александр Георгиевич, д-р физ.-мат. наук, профессор, ВолгГТУ, г. Волгоград.
Горобцов Александр Сергеевич, д-р техн. наук, профессор ВолгГТУ, г. Волгоград.
Библиографическая ссылка
Русаков С.А., Муха Ю.П. МЕТОДИКА ОПРЕДЕЛЕНИЯ ОСЕВОЙ ЖЕСТКОСТИ КОСТНОГО РЕГЕНЕРАТА // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=9144 (дата обращения: 27.04.2024).



