За последние полтора десятилетия интерактивные компьютерные модели вошли в систему физического образования в качестве одного из средств обучения. Однако их дидактическая ценность, целесообразность применения при различных формах организации занятий и возможности использования в различных видах учебной деятельности оцениваются весьма по-разному различными дидактами, методистами и практикующими педагогами, о чем свидетельствуют дискуссии на научно-методических конференциях.
На наш взгляд, различие оценок в значительной степени связано с тем, что речь о компьютерных моделях ведется как об однородном множестве, тогда как они существенно отличаются не только с точки зрения дисциплинарного содержания и дизайна, но и с точки зрения их места в процессе познания. Представляется, что упомянутые дискуссии могут стать более конструктивными в контексте предлагаемой классификации компьютерных моделей, соответствующей традиционной структуре естественнонаучного исследования, с которым процесс учения во многом схож.
Физика изучает и помогает изменять реальный мир, но знания, являющиеся результатом исследования этого мира, и рецепты его изменения обычно формулирует на языке моделей. Поэтому говорят, что физика – это наука о моделях. Моделями с точки зрения познания являются физические понятия (объекты, которыми оперирует теория, и их характеристики, включая физические величины) и отдельные физические законы. Из кирпичиков понятий и законов строятся модели физических явлений. Моделями являются целые физические теории. В философских и физических работах моделирование рассматривается как один из общих методов научного исследования, а модель – как средство получения знания [4,8].
Рассмотрению закономерностей процесса познания в физике, изучению роли и соотношения экспериментального и теоретического уровней исследования посвящено большое число работ, наиболее фундаментальной из которых представляется монография [3]. Преломление процесса научного познания в образовательном процессе обсуждается в учебном издании [6]. Процедуру построения модели физического объекта или явления принято подразделять на ряд этапов. Соответствующую структуру процесса познания в физике, предложенную в [3], изобразим в виде следующей схемы (рис. 1).
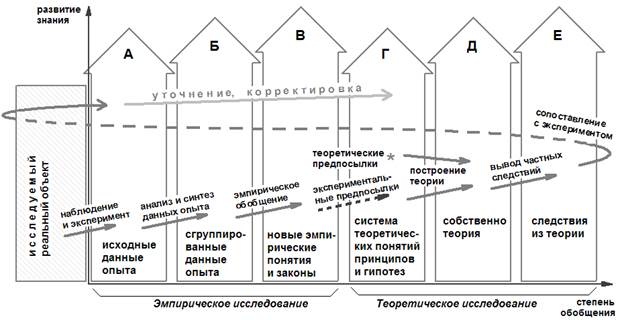
Рис. 1. Этапы процесса познания в физике и интеллектуальные действия исследователя
В столбцах А-Е представлены элементы эмпирического и теоретического знания, над стрелками переходов от одного столбца к другому надписаны совершаемые исследователем при этих переходах интеллектуальные действия. Каждый переход приводит к повышению степени обобщения знания. Последнее действие замыкает элемент Е на элемент А, так что образуется циклический процесс.
Отметим, что переходы на рисунке от одного элемента знания к другому (в том числе и первая стрелка – от объекта исследования к опытным данным) являются, по сути, актами моделирования определенного уровня: А-Б – моделирование причинно-следственных связей (например, в форме таблиц экспериментальных данных); Б-В – создание моделей эмпирических понятий и законов (понятий давления или силы тока, законов Шарля или Ома); В-Г – уточнение существующих и введение новых, теоретических понятий (например, введение понятий идеального газа и молекулярного хаоса, раскрытие статистического смысла понятий давления и температуры в молекулярно-кинетической теории); Г-Д – построение теоретических законов (например, основного уравнения молекулярно-кинетической теории газов) и так далее.
В последние десятилетия в физических исследованиях все чаще используются компьютерные технологии. Раньше всего они были внедрены в этапы А-Б-В – в качестве средства автоматизации и обработки результатов эксперимента, а также в этап Е-А – в качестве средства расчета сложных задач, являющихся частными случаями или следствиями теории. Появилось понятие численного моделирования (вычислительного эксперимента).
Позднее, когда компьютерные технологии стали применяться в обучении, появились моделирующие учебные программы. Компьютерные модели учебного назначения, как и научно-исследовательские, можно классифицировать в соответствии с этапами познания, к которым они относятся, и с исполняемыми ими гносеологическими функциями. Следуя, в целом, работам [4, 8], выделим такие функции моделей в процессе познания:
– аппроксимационная: отражение действительности с некоторым огрублением, упрощением («выделение существенного с целью выяснения существенного») и с последующим итерационным ростом адекватности модельного описания явления, дополняемым элементами его объяснения;
– заместительно-эвристическая: выполнение роли одной из ступеней в процессе познания, промежуточного звена между теоретическим абстрактным мышлением и объективной действительностью, открытие новых путей развития теории;
– экстраполяционно-прогностическая: перенос свойств модели на изучаемый объект, построение и проверка теории, открытие пути подтверждающему эксперименту (формулировка условий его осуществления) и объяснение явления (установление причинных и закономерных связей, раскрытие их сущности);
– трансляционная: отражение реальности путем переноса информации с одной, изученной сферы на другую, не изученную, но имеющую существенные черты сходства с первой;
– иллюстративная: демонстрация явления с целью установления связи между чувственным и логическим, конкретным и абстрактным (с элементами объяснения).
В соответствии с рис. 1 выделим шесть классов учебных компьютерных моделей.
1. Интерактивная компьютерная модель, соответствующая фазе А-Б-В на рис. 1, является достойным объектом учебного исследования, если исходная информация поступает на компьютер с реальной экспериментальной установки. По сути, это полноценный физический эксперимент, в котором компьютер выполняет роль одного из инструментов.
Если же речь идет о сугубо «виртуальном» представлении физических объектов (явлений, понятий, законов, свойств), которое обычно и предлагается компьютерными учебными изданиями, то такие модели уязвимы по отношению к критике со стороны противников использования компьютера. На самом деле эти модели обычно соответствуют цепочке В-А-Б-В, содержащей «порочный» участок «возвратного движения», поскольку имеют в своей основе готовый эмпирический закон, а пользователь в ходе модельного эксперимента «заново открывает» его. Эмпирический закон обычно отражает лишь внешние связи между величинами и потому математически прост. Соответственно, модель состоит из одного – двух уравнений и имеет малое число степеней свободы, так что ее «исследование» превращается в банальную табуляцию явной зависимости. Никакие искусственные приемы типа внесения «экспериментальной погрешности» не повышают заметно ценность таких моделей для развития мышления учащегося. Впрочем, ценность эта не нулевая благодаря одному из важнейших присущих модели свойств – наглядности. Модель, создающая яркий, запоминающийся образ, выполняет иллюстративную функцию, и ее применение в качестве демонстрации может быть оправданным при изложении нового материала.
Поскольку пользователь в ходе модельного эксперимента анализирует данные, обнаруживает закономерности, назовем эти модели регуляризирующими (от английского to regularaze – упорядочивать) или эмпирикоподобными 1-го рода.
Говорить же об исследовании на основе компьютерной модели можно лишь в том случае, если эта модель не содержит в себе готового результата. Для этого она должна описывать систему, уравнения которой решить «на руках» сложно или практически невозможно. Например, если процесс, описываемый моделью, многофакторный, многоэтапный, если велико количество задействованных в нем тел, то наблюдение и обобщение данных на выходе из компьютера будет содержательным, а не имитирующим.
2. Более содержательны модели, также имитирующие фазу А-Б-В, но включающие цепочку Г-А-Б-В, то есть имеющие в своей основе теоретические законы наряду с экспериментальными законами и понятиями. Такие модели могут иметь значительное число степеней свободы. Они не содержат готового результата, поведение их не является однозначным. Тем не менее вполне признанным педагогической общественностью является лишь модельный вариант исторических реконструкций классических экспериментов, когда модель определенно не уступает учебному фильму, а при качественном (в визуальном и содержательном плане) исполнении существенно превосходит его за счет интерактивности. С оговорками оправданным считают компьютерный эксперимент, «прототип» которого по какой-либо причине невозможен в учебной лаборатории, дорог или опасен (движение небесных тел, ядерные реакции и пр.). Представление же в компьютерной среде моделей-аналогов обычного лабораторного эксперимента, особенно схожих по интерфейсу с реальными установками, в большинстве случаев вызывает негативные оценки экспериментаторов, хотя и этот вариант продуктивен, если акцент делается на визуализации невидимых элементов системы и абстрактных понятий (векторы сил, силовые линии полей, индукционный ток). На таких моделях можно ставить задания, схожие с познавательной точки зрения с традиционными лабораторными работами. Кроме того, они могут быть частью некоторого обучающего сценария. Модели этого класса можно назвать инференционными (от to infer – выводить заключение) или эмпирикоподобными 2-го рода.
3. Весьма интересными и перспективными для использования в обучении представляются интерактивные модели, соответствующие этапу В-Г (или внутренние для фазы Г, имеющей сложную внутреннюю структуру) рис. 1, нацеленные на формирование новых, теоретических или раскрытие содержания уже известных, эмпирических понятий, на уточнение оснований новой теории. Такие компьютерные модели не служат заменой реального физического эксперимента, а являются самоценными для процесса познания. Например, серия модельных экспериментов, описанных в [1, 2, 7], позволяет, основываясь на понятии идеального газа и механической модели (законы сохранения и второй закон Ньютона) теплового движения молекул, сформулировать на микроуровне понятие термодинамического равновесия, изучить свойства молекулярного хаоса, раскрыть статистический смысл понятий давления и температуры.
На этом же этапе познания в физике часто проводят так называемый мысленный эксперимент, представляющий собой обобщение реальных экспериментов в идеализированных (читай – модельных) условиях. Таким образом, мысленный эксперимент – это моделирование реального физического явления. Применение же компьютера позволяет визуализировать результат этого моделирования, сопоставить и «привести к общему знаменателю» представление о процессе у группы пользователей. Минус такой технологии донесения информации до учащихся состоит в том, что разработчик программного обеспечения, по сути, навязывает пользователю свое видение процесса как некоторого шаблона. Однако этот субъективизм разработчика является и благом, поскольку информация становится конкретной, наглядной, «измеряемой», тогда как в отсутствии подобного шаблона учителю очень непросто убедиться, что в мозгу учащихся сформировались хоть какие-то представления о «помысленном» явлении. К тому же, приняв «шаблонный» вариант за начальный уровень, грамотный учитель может высказать свои замечания и уточнения к используемой модели, чтобы поднять качество представлений учащихся на большую высоту.
Описанные модели, призванные углубить систему научных представлений пользователя, назовем иммерсионными (от to immerse – погружаться, уходить с головой) или теоретикоподобными 1-го рода.
4. Отражение в компьютерной среде фазы Г-Д может быть сложным и даже невозможным. Однако в ряде случаев модельный эксперимент позволяет не только обнаружить важные зависимости на качественном уровне, но и вскрыть их причину и смысл, избежав при этом математических сложностей, сопутствующих строгому решению проблемы. В [1, 2, 7] примерами такого рода являются «вычисление» общего (нулевого) начала термодинамики (самопроизвольный переход замкнутой системы в состояние термодинамического равновесия) и основного уравнения молекулярно-кинетической теории газов на основе уже упоминавшейся механической модели теплового движения. Модели такого рода, требующие исследовательского подхода, отнесем к классу инвентивных (от to invent – придумывать, создавать, изобретать) или теоретикоподобных 2-го рода.
5. Богатые возможности для развития физических представлений и теоретического мышления предоставляет фаза Д-Е. Системы модельных объектов, поставленные в определенные условия и наделенные определенными значениями параметров, способны проявлять новые качества и обнаруживать специфические свойства. Например, та же механическая модель теплового движения в газах позволяет отследить динамику установления распределения Максвелла по скоростям, изучить его зависимость от температуры. Среди других следствий этой модели такие важные теоретические положения, как эргодическая гипотеза (эквивалентность осреднения характеристик по времени и по ансамблю частиц), теорема о равномерном распределении кинетической энергии по степеням свободы, распределение Больцмана частиц по потенциальным энергиям, закономерности броуновского движения, согласующиеся с теорией Эйнштейна – Смолуховского. Модели этого класса могут быть названы детектирующими (от to detect – замечать, открывать) или эвристическими.
Принципиальное отличие моделей двух последних классов от эмпирикоподобных моделей состоит в том, что от пользователя требуется не просто определить некую величину или обнаружить тенденцию, изначально заложенную в модель, но выявить глубинные механизмы, которые эту тенденцию обеспечивают, открыть принципиально новую сущность, новое качество, не содержащиеся в уравнениях модели в явном виде. Между собой инвентивные и детектирующие модели отличаются тем, что первые позволяют выявить наиболее общие, базовые сущности, вторые же – различные частные, хотя и важные проявления этих сущностей.
6. Весьма ценными для развития мышления учащихся представляются модели, учебная деятельность в рамках которых соответствует этапу Е-А, этапу сопоставления модели с экспериментом. На их основе можно поставить полноценное исследование, в том числе дать прогноз поведения системы в еще не изученных экспериментально ситуациях и даже просчитать условия, при которых в эксперименте удастся обнаружить новый эффект. К недостаткам моделей такого рода можно отнести сложность представления результатов в аналитическом виде, но тенденции, качественные закономерности явлений видны отчетливо; в ряде случаев возможны прямые сравнения расчетных значений с экспериментом. Назовем модели этого класса компаративными (от to compare – сравнивать) или прогностическими.
Особенности, функции и целесообразные способы использования моделей описанных классов сведены в таблицу 1.
Таблица 1. Соответствие этапов познания классам моделей и их характеристикам
|
Этап процесса познания |
Содержание деятельности |
Способ мышления |
Ведущие функции модели на этапе |
Возможная форма использования |
Класс модели |
|
В-А-Б-В |
обобщение данных, поиск закономерности |
индук-тивный |
иллюстративная |
демонстрация |
регуляризирующие (эмпирикоподоб-ные 1-го рода) |
|
Г-А-Б-В |
обобщение данных, поиск закономерности |
индук-тивный |
экстраполяционно-прогностическая, иллюстративная |
лабораторный стенд, демонстрация |
инференционные (эмпирикоподоб-ные 2-го рода) |
|
В-Г, Г |
обнаружение, углубление смысла понятий |
индук-тивный |
аппроксимационная, трансляционная |
исследование, демонстрация |
иммерсионные (теоретикоподоб-ные 1-го рода) |
|
Г-Д |
выявление новой сущности (построение теории) |
индук-тивный |
заместительно-эвристическая |
исследование, лабораторный стенд, демонстрация |
инвентивные (теоретикоподоб-ные 2-го рода) |
|
Д-Е |
выявление связанных сущностей (следствий |
дедук-тивный |
заместительно-эвристическая, экстраполяционно-прогностическая |
исследование, лабораторный стенд, демонстрация |
детектирующие (эвристические) |
|
Е-А |
сопоставление результатов моделирования и эксперимента |
дедук-тивный |
экстраполяционно-прогностическая |
лабораторный стенд, демонстрация |
компаративные (прогности-ческие) |
Отметим, что в четвертом столбце таблицы указаны не все, а лишь основные функции, выполняемые моделью на каждом этапе познания. Например, иллюстративная функция присуща моделям всех классов, но указана она лишь у двух из них.
В целом из таблицы видно, что интерактивные компьютерные модели разных классов имеют существенные отличия, касающиеся вида поддерживаемых ими интеллектуальных действий, способов построения умозаключений, адекватной формы использования при обучении. Обсуждать полезность, целесообразность и условия эффективного использования компьютерных моделей следует с учетом их функций и места в процессе познания.
Подавляющее большинство моделей, входящих в состав существующих сегодня электронных учебных пособий, являются, по нашей классификации, эмпирикоподобными. Их достоинства – яркая иллюстративность, а также доступность в использовании как педагогом, так и учащимся. При этом они не отличаются глубиной, их возможности в плане развития мышления и формирования научных представлений невелики. Развивающий потенциал моделей остальных классов, напротив, высок, но эти модели относительно малочисленны, а вопросы их разработки и методики использования хотя и обсуждаются в научно-методических публикациях (например, [1,2,5]), но требуют дальнейшего изучения.
Рецензенты:
Оспенникова Елена Васильевна, д-р пед. наук, профессор, зав. кафедрой мультимедийной дидактики и информационных технологий обучения Пермского государственного гуманитарно-педагогического университета, г. Пермь.
Косолапова Лариса Александровна, д-р пед. наук, доцент, зав. кафедрой педагогики Пермского государственного гуманитарно-педагогического университета, г. Пермь.
Библиографическая ссылка
Баяндин Д.В. КЛАССИФИКАЦИЯ ИНТЕРАКТИВНЫХ КОМПЬЮТЕРНЫХ МОДЕЛЕЙ И СТРУКТУРА ПРОЦЕССА ПОЗНАНИЯ В ФИЗИКЕ // Современные проблемы науки и образования. 2013. № 2. ;URL: https://science-education.ru/ru/article/view?id=9018 (дата обращения: 20.12.2025).



