Введение
Основным способом финишной обработки закаленных деталей являются процессы шлифования, среди которых около 27% приходится на операции плоского шлифования периферией круга. На сегодняшний день проектирование операций плоского шлифования осуществляется по нормативным справочникам [4], которые являются результатом статистической обработки технологических процессов, применяемых на машиностроительных предприятиях страны до 1991 года. По существу, заложенная в них методика является укрупненной и в большей степени направлена на определение трудоемкости изготовления детали, т.е. решается вопрос нормирования операции. Это предопределило основной недостаток методики назначения режимов резания: жесткое задание количества рабочих ходов и постоянство глубины резания на них, обеспечивающей отсутствие прижогов и выполнение требований по шероховатости готовой детали даже на начальных этапах обработки.
В результате на производстве технология обработки конкретной детали корректируется по точности, шероховатости, бесприжоговости, производительности и другим критериям. Такое положение приводит к существенному увеличению периода технологической подготовки производства, что в совокупности с низкой производительностью приводит к существенным экономическим потерям.
В то же время для повышения производительности операций круглого шлифования эффективно применяются циклы, при которых весь путь инструмента к детали делится на ступени с различающейся радиальной подачей [3]. При этом имеется возможность адаптировать цикл обработки к конкретным технологическим условиям. Поскольку при плоском шлифовании подача на двойной рабочий ход является дискретной, то управление параметрами операции возможно за счет разбиения припуска на стадии обработки и оптимизации количества рабочих ходов на каждой из них.
Оптимизация возможна на основе модели процесса, учитывающей его разноплановые физические особенности: множественное вероятностное микрорезание, высокую теплонапряженность и упругие отжатия в технологической системе. Поскольку механическое взаимодействие инструмента и заготовки является первостепенным в сложной последовательности теплофизических и силовых взаимосвязей, то базой моделирования процесса должна являться геометрическая модель съема припуска. Использование модели позволит расчетным путем находить параметры шероховатости на каждом рабочем ходе и тем самым формировать набор исходных данных, необходимых для расчета температур и сил резания. Все существующие модели шероховатости не учитывают полученный на предыдущих рабочих ходах микрорельеф и поэтому не могут быть использованы.
Моделирование процесса шлифования представляется последовательным использованием геометрической, теплофизической и силовой моделей. При этом входные данные для каждой из них являются результатами моделирования предыдущей. Это диктует необходимость создания комплексной модели плоского шлифования периферией круга.
1. Модель формирования шлифованной поверхности и съема припуска.
Расчетная схема модели формирования шлифованной поверхности приведена на рис. 1. Поверхностный слой круга движется со скоростью круга – VK, относительно заготовки, движущейся со скоростью VЗ. В зоне контакта абразивные зерна врезаются в поверхностный слой детали на различную величину, срезая при этом некоторый объем металла и оставляя шлифовальную риску. В результате наложения множества рисок друг на друга образуется новая поверхность детали с расположенными на ней неровностями. На втором рабочем ходе зерна врезаются в уже обработанный материал, имеющий неровности, и формируют поверхность с отличающимся микрорельефом.
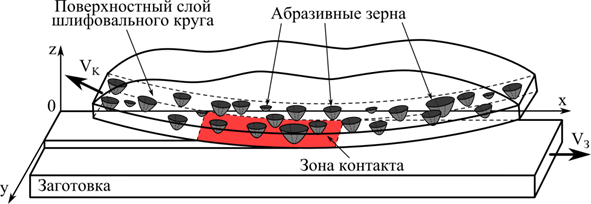
Рис. 1. Расчетная схема геометрической модели
На основе анализа работ [2; 3] в качестве аппроксимирующей фигуры формы абразивного зерна принят эллиптический параболоид вращения, обеспечивающий максимальное приближение и имеющий возможность учета зернистости и износа. Поэтому образуемая зерном поверхность риски формируется наиболее выступающей частью абразивного зерна – параболой, движущейся по окружности – периферии инструмента (рис. 2).

Рис. 2. Расчетная схема для определения рельефа единичной риски
Расчет поверхности, образованной зерном, осуществляется в два этапа: разделение риски по длине на множество сечений с шагом Δ и, исходя из высоты расположения параболы в каждом сечении, расчет координат точек параболы по высоте:
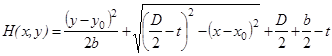 ,
, ![]() ,
, ![]() , (1)
, (1)
где D – диаметр круга, t – глубина внедрения зерна, b – параметр, характеризующий размер зерна, x0 и y0 – координаты риски на поверхности детали, l и c –длина и ширина риски.
Для расчетного построения поверхности заготовки в результате наложения множества единичных рисок, построенных по (1), необходимо задаться моделью строения абразивного инструмента. На основе существующих исследований принято условие случайного нормального распределения размеров абразивных зерен bi и их равномерного распределения в поверхностном объеме инструмента диаметром D, высотой B и толщиной H. Зная координаты расположения зерен и скорости взаимного движения инструмента и заготовки, имеется возможность определения координат расположения рисок на детали. Таким образом, происходит последовательное наложение рисок на деталь и формирование готовой поверхности.
В итоге рельеф поверхности детали формируется в результате наложения k рисок друг на друга по методу суперпозиции, т.е. каждый элемент матрицы детали есть минимальная высота расположения поверхности в данном узле из всей совокупности рисок:
![]() (2)
(2)
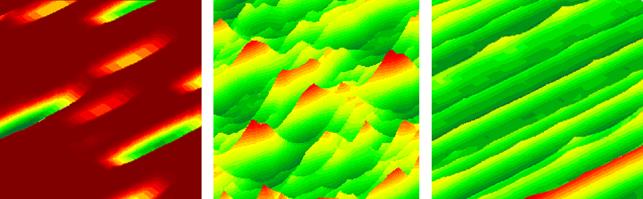
Образованная поверхность переходит на следующий рабочий ход, в процессе которого формируется новая поверхность с учетом предшествующего микрорельефа. Таким образом, имеется возможность построить микрорельеф шлифованной поверхности на каждом рабочем ходе операции плоского шлифования (рис. 3).
 |
||
|
а) |
б) |
в) |
Рис. 3. Микрорельеф шлифованной поверхности на рабочем ходе:
а) касания круга и заготовки; б) активного резания; в) выхаживания
Расчет показателей шероховатости осуществляется путем выбора на поверхности детали N поперечных сечений, математически представленных столбцами матрицы. В каждом столбце на базовой длине рассчитывается наиболее распространенный показатель шероховатости, применяемый в технологии обработки металлов резанием, среднеарифметическое отклонение профиля, определяемое следующим образом:
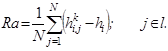 (3)
(3)
Адекватность разработанной модели подтверждается сопоставлением с экспериментальными данными при 95%-ном уровне доверительной вероятности.
2. Формирование комплексной имитационной модели
Разработка теплофизической и силовой моделей, построенных на схеме дискретного вероятностного контакта, является сложной задачей, требующего отдельного решения. Поэтому для прогнозирования выбирается уже существующая модель А.А. Дьяконова [1], а задача формирования комплексной модели сводится к объединению разработанной модели шероховатости и моделей А.А. Дьяконова.
Геометрическая модель поставляет для теплофизической следующие исходные данные: количество микроконтактов зерна с шероховатой поверхностью, координаты этих контактов, глубина резания и трения в каждом из них, объем снятого металла, характер взаимодействия (резание или деформирование), время микроконтакта. Отметим, что до объединения с геометрией микрорезания представленные исходные данные задавались пользователем. Затем каждый микроконтакт представляется тепловым источником и точкой приложения силы резания от единичного зерна. Таким образом, имеем возможность прогнозировать микрорельеф поверхности, температурные поля и силы резания в одной комплексной модели.
На рис. 7 представлена структурная схема комплексной имитационной модели. Блоки и взаимосвязи, выделенные жирными рамками, были разработаны впервые. На основе заданных пользователем параметров инструмента – зернистости, структуры, размеров и прочих параметров строится абразивный инструмент, являющийся основой для расчета микрорельефа обработанной поверхности. В свою очередь, полученные в процессе построения обработанной поверхности данные являются исходными для теплофизической модели процесса. Температурные поля и данные о механическом взаимодействии являются исходными для расчета сил резания от каждого абразивного зерна, суммирование которых позволяет найти радиальную составляющую силы резания и возникающие отжимы.
В результате реализации представленного комплекса на языке программирования C++ стало возможным моделировать любую стадию обработки плоским шлифованием с прогнозированием микрорельефа обработанной поверхности и ее шероховатости, температурных полей и сил резания. Именно объединение частных моделей в комплекс позволило избавиться от необходимости задания промежуточных сложных для определения исходных данных, оставив в качестве требуемых исходных данных только общепринятые технологические параметры: скорости движения, размеры, параметры инструмента и процесса.
Сопряжение теплофизической и силовой моделей с геометрической также позволило приблизить результаты моделирования к экспериментальным данным, полученным А.А. Дьяконовым [1].
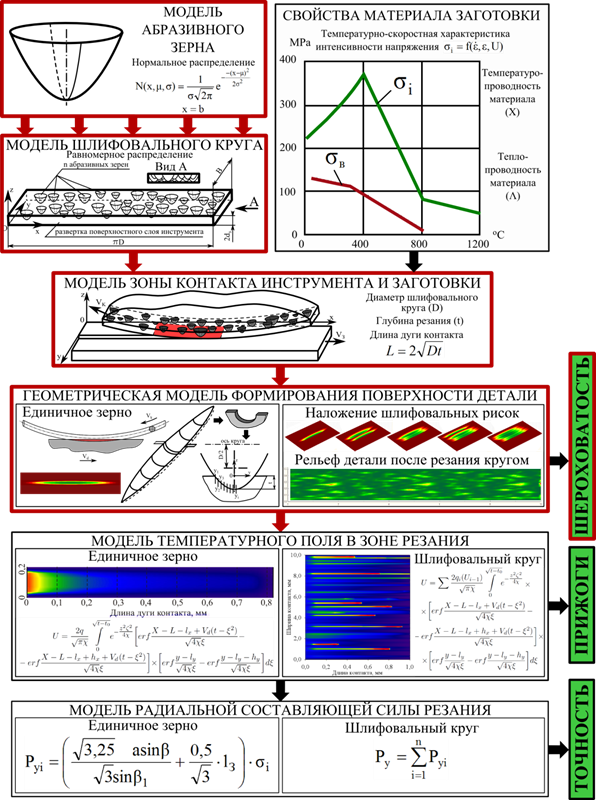
Рис. 4. Структурная схема комплексной имитационной модели
3. Совершенствование методики проектирования операций плоского шлифования.
Научно-методическая база совершенствования методики основывается на делении припуска на стадии, наложении на них различных ограничений и определение режимов резания.
На первой стадии снимается большая часть припуска за исключением оставленного дефектного слоя (рис. 5). Активными технологическими ограничения на этой стадии являются прикладываемая к зерну и к связке сила резания и температура, вызывающая прижог не более оставшегося припуска:
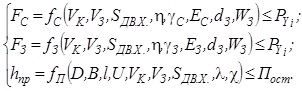 (4)
(4)
Целью второй стадии обработки является снятие дефектного слоя, образовавшегося на предыдущей стадии, и выполнение размерной точности обработки за счет уменьшения сил резания и упругих отжатий. Технологическими ограничениями на этой стадии являются отсутствие прижога на поверхности и выполнение размерной точности обработки.
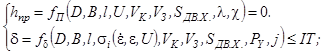 (5)
(5)
Третья стадия обработки направлена на формирование заданной шероховатости. Прижоги на данной стадии исключены, поэтому рассматривается лишь технологическое ограничение по шероховатости:
![]() (6)
(6)
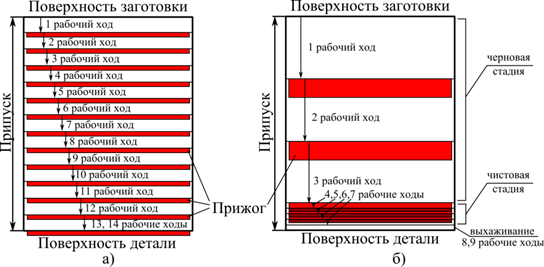
Рис. 5. Деление припуска: по нормативам (а) и по разработанной методике (б)
Полученные системы уравнений (4–6) есть математическая постановка задачи оптимизации количества рабочих ходов на стадиях обработки. Эта задача относится к задачам математического программирования. В соответствии с формальным аппаратом математического программирования по каждому ограничивающему параметру определяется область допустимых параметров управления. Пересечение областей определяет область, гарантирующую выполнение всех требований на соответствующей им стадии обработки (рис. 6). Область не вырождается в точку, поэтому вводится критерий оптимальности – минимум основного времени tо.
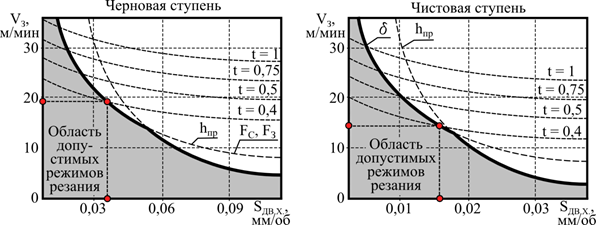
Рис. 6. Области допустимых режимов резания для черновой и чистовой стадий обработки
Разработанная научно-методическая база оптимизации количества рабочих ходов на стадиях обработки реализована в виде расчетного алгоритма (программы) и инженерной методики (карты и таблицы решения). Разработанные рекомендации по бездефектным режимам операций плоского шлифования периферией круга оформлены в виде руководящих технических материалов, которые внедрены на ряде предприятий Уральского региона. Результаты внедрения и проведенный эксперимент позволяют говорить о повышении производительности операций плоского шлифования до 220%.
Рецензенты:
Гузеев Виктор Иванович, доктор технических наук, профессор, заведующий кафедрой «Технология машиностроения», ФГБОУ ВПО «Южно-Уральский государственный университет» (НИУ), г. Челябинск.
Переверзев Павел Петрович, доктор технических наук, профессор, профессор кафедры «Технология машиностроения», ФГБОУ ВПО «Южно-Уральский государственный университет» (НИУ), г. Челябинск.
Библиографическая ссылка
Шипулин Л.В. СОВЕРШЕНСТВОВАНИЕ МЕТОДИКИ ПРОЕКТИРОВАНИЯ ОПЕРАЦИЙ ПЛОСКОГО ШЛИФОВАНИЯ ПЕРИФЕРИЕЙ КРУГА НА ОСНОВЕ КОМПЛЕКСНОГО МОДЕЛИРОВАНИЯ ПРОЦЕССА // Современные проблемы науки и образования. 2013. № 2. ;URL: https://science-education.ru/ru/article/view?id=9014 (дата обращения: 07.07.2025).



