Современный этап развития энергосистем характеризуется повышением требований к качеству прогнозирования потребления электроэнергии в условиях существенного ограничения на выделяемые энергоресурсы. Актуальными становятся проблемы разработки и внедрения энергосберегающих технологий, нечувствительных к недостатку априорной информации, применение новых методов прогнозирования.
Наряду со статистическими методами в настоящее время используются нечеткие и нейросетевые системы искусственного интеллекта, которые, будучи универсальными аппроксиматорами, гарантируют возможность успешного прогнозирования. Основные преимущества интеллектуальных систем прогнозирования: способность получения правильного решения задачи при наличии неполных и искаженных данных после настройки параметров (обучения) сети; возможность учета большого количества дополнительных факторов, влияющих на качество прогнозирования. Недостаток интеллектуальных систем – необходимость обучения. Отрицательное свойство нейронечетких сетей – при наличии более пяти входов реализация становится очень сложной, точность решения уменьшается; негативная особенность нейронных сетей – сложность поиска неисправности.
В последние годы при использовании метода опорных векторов новое развитие получил способ прогнозирования на основе регрессионных моделей, альтернативный интеллектуальному подходу.
Преимуществом метода опорных векторов [8] (SVM–support vector machines) является то, что параметры регрессионной модели определяются на основе решения задачи квадратичного программирования, имеющей единственное решение.
Ограничение использования метода опорных векторов связано с отсутствием рекомендаций по выбору параметров ядерной функции, наиболее подходящих для решения конкретной задачи. Необходимо проведение дополнительных исследований для определения эффективных параметров алгоритма.
В настоящей работе предлагается с целью повышения точности прогнозирования электропотребления использовать метод опорных векторов, оптимизационные генетические алгоритмы [5] (GA – genetic algorithm) и алгоритмы роя частиц [6] (PSO – particles warm optimization).
Задача прогнозирования формулируется следующим образом:
зная предыдущие q (длина окна) значений временного ряда, предсказать последующее значение x(t+d):
![]() (1)
(1)
где d – шаг прогнозирования, g – количество независимых переменных h.
Для формирования обучающей последовательности временной ряд при этом выглядит следующим образом:
![]()
![]()
Задачей построения уравнения регрессии является оценка неизвестной вещественной функции:
![]()
где ![]() , вектор w
, вектор w![]() и смещение
и смещение![]() – параметры уравнения, e – ограниченные неучтенные возмущения, для задачи (1)
– параметры уравнения, e – ограниченные неучтенные возмущения, для задачи (1)![]() .
.
В методе опорных векторов задача построения нелинейной регрессии в исходном пространстве F рассматривается как задача построения линейной регрессии в некотором расширенном пространстве признаков H, порождаемом нелинейным отображением f: F®H
f(x)=(w, f(x))+w0
Задача нахождения параметров (поиска оптимальной разделяющей поверхности) сводится к задаче квадратичной оптимизации и формулируется в виде минимизации функционала:
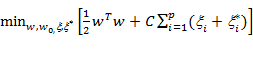 (2)
(2)
при ограничениях
![]()
Здесь параметр С – положительная константа, чем больше значение С, тем выше штраф ошибки, xi – параметры для обработки неразделимых наблюдений (входов), e – функции потерь. Штрафное слагаемое в функционале![]() вводится согласно принципу регуляризации и означает, что среди всех векторов w, минимизирующих функционал (2), наиболее предпочтительны векторы с минимальной нормой. Второе слагаемое функционала штрафует любые отклонения f(x) от
вводится согласно принципу регуляризации и означает, что среди всех векторов w, минимизирующих функционал (2), наиболее предпочтительны векторы с минимальной нормой. Второе слагаемое функционала штрафует любые отклонения f(x) от![]() , больше чем e для всех обучающих данных.
, больше чем e для всех обучающих данных.
При использовании метода опорных векторов обычно решается двойственная к данной задача [1; 2; 4].
![]() ,
,
где двойственные переменные удовлетворяют условию![]() , K (xi, x) – ядерная функция. В исследованиях в качестве ядерной функции использована гауссова радиальная базисная функция:
, K (xi, x) – ядерная функция. В исследованиях в качестве ядерной функции использована гауссова радиальная базисная функция:
K(x, x′) = exp (![]() ) (3)
) (3)
Идея алгоритма роя частиц частично заимствована из исследований поведения скоплений животных (косяков рыб, стай птиц и т.п.). Метод является стохастическим, не требующим вычисления градиента, может использоваться для решения многих задач, включая обучение нейросетей, задачи поиска минимума функции, а также задач для оптимизации опорных векторов.
Алгоритм имитирует передвижения птиц в пространстве поиска, каждая птица – «частица». Частицы передвигаются с определенной скоростью до тех пор, пока не будет найдена позиция глобального оптимума.
Расчет вектора скорости i-й частицы на t+1 шаге может быть вычислен в соответствии со следующими формулами:
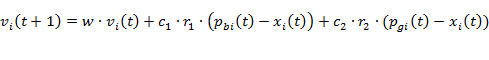 (4)
(4)
![]()
Скорость зависит от трех членов. Первый – ![]() . Множитель w – инерционный вес и является константой;
. Множитель w – инерционный вес и является константой; ![]() – текущая скорость i-й частицы в момент t. Второй член –
– текущая скорость i-й частицы в момент t. Второй член –![]() . Множитель
. Множитель![]() =const,ускорение с положительными значениями, называемый локальной весовой долей. Множитель
=const,ускорение с положительными значениями, называемый локальной весовой долей. Множитель![]() является случайной переменной в диапазоне [0,1]. Векторная величина
является случайной переменной в диапазоне [0,1]. Векторная величина![]() – это лучшая позиция i-й частицы, а векторная величина
– это лучшая позиция i-й частицы, а векторная величина![]() – текущая позиция i-й частицы. Если f – функция, которую необходимо минимизировать, тогда выражение для
– текущая позиция i-й частицы. Если f – функция, которую необходимо минимизировать, тогда выражение для![]() зависит от времени:
зависит от времени:
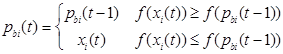
Третий член в уравнении обновления скорости – ![]() . Множитель
. Множитель ![]() является константой, называемой глобальной весовой долей. Множители
является константой, называемой глобальной весовой долей. Множители ![]() и
и ![]() одинаковы. Величина вектора
одинаковы. Величина вектора![]() – глобальная лучшая позиция всего роя частиц.
– глобальная лучшая позиция всего роя частиц. ![]() – фактор ограничения, использующийся для контроля веса скорости.
– фактор ограничения, использующийся для контроля веса скорости.
Блок-схема алгоритма выглядит следующим образом (рис. 1):
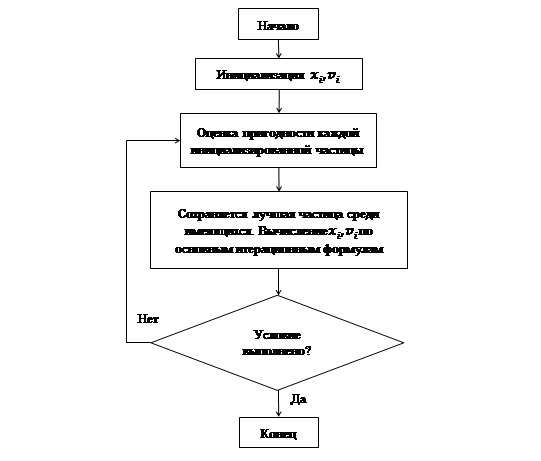
Рис. 1
Метод генетических алгоритмов – поисковые алгоритмы стохастической оптимизации, основанные на механизмах генетики (генетического наследования и естественного отбора), в которых сохраняется в упрощенном виде биологическая терминология.
Генетический алгоритм предполагает выполнение следующих шагов.
Шаг 1. Создать обучающее множество векторов и тестовое множество векторов.
Шаг 2. Создать исходную популяцию. Каждая особь состоит из двух хромосом – значения параметров ![]() и s.
и s.
Шаг 3. Вычислить функции пригодности для особей популяции.
Шаг 4. Выбор родителей для процесса размножения (оператор селекции – репродукции).
Шаг 5. Создание потомков выбранных пар родителей (оператор скрещивания).
Шаг 6. Мутация новых особей.
Шаг 7. Расширение популяции за счет добавления новых особей.
Шаг 8. Сокращение расширенной популяции до исходного размера (оператор редукции).
Шаг 9. Процесс продолжается до тех пор, пока критерий остановки не будет выполнен. Иначе переход на шаг 3.
Метод главных компонент [7] (PCA – principle component analysis) – один из основных способов уменьшения размерности данных с потерей минимального количества информации. Он состоит в линейном ортогональном преобразовании входного вектора x размерности q в выходной вектор y размерности s, где ![]() . При этом компоненты вектора y являются некоррелированными, и общая дисперсия после преобразования остается неизменной. Совокупность входных данных обучающей выборки представима в виде матрицы:
. При этом компоненты вектора y являются некоррелированными, и общая дисперсия после преобразования остается неизменной. Совокупность входных данных обучающей выборки представима в виде матрицы:
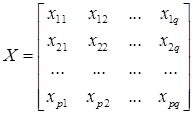
где p – количество обучающих выборок.
Пусть R ковариационная матрица (размерности ![]() ) входных данных x,
) входных данных x,![]() – собственные числа,
– собственные числа, ![]() – соответствующие им единичные собственные векторы. Метод главных компонент состоит в нахождении таких линейных комбинаций исходных переменных:
– соответствующие им единичные собственные векторы. Метод главных компонент состоит в нахождении таких линейных комбинаций исходных переменных:
![]() i=1,…,s,
i=1,…,s,
s – число главных компонент.
Переменные уi упорядочены по возрастанию дисперсии, большую часть общей дисперсии характеризует подмножество s первых переменных. Относительные доли дисперсии исходных данных определяются по формуле: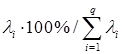 . В матричной форме преобразование главных компонент можно представить как y = Ux.
. В матричной форме преобразование главных компонент можно представить как y = Ux.
Обучающая выборка представляет собой почасовые данные электропотребления за 5 рабочих дней весеннего периода 2009 года. Выполнено предварительное нормирование данных обучающей выборки так, чтобы они находились в диапазоне [0,1]. Нормированные данные обрабатываются методом главных компонент (функция MATLAB princomp).
В исследовании для подбора параметров ![]() функционала (2) и параметра ядерной функции s (3) выбраны параметры алгоритма роя частиц (4)
функционала (2) и параметра ядерной функции s (3) выбраны параметры алгоритма роя частиц (4)![]() =1.5,
=1.5, ![]() =1.7, количество частиц – 20, максимальное количество итераций – 100, w=0,8,
=1.7, количество частиц – 20, максимальное количество итераций – 100, w=0,8, ![]() =1,
=1,![]() ,
,![]() получат от функции MATLAB rand; параметр
получат от функции MATLAB rand; параметр ![]() и s выбирается из диапазона [0; 100]. Функция пригодности задается как
и s выбирается из диапазона [0; 100]. Функция пригодности задается как 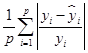 , где
, где ![]() ,
,![]() обозначает фактические и расчетные значения прогноза.
обозначает фактические и расчетные значения прогноза.
Исследование моделированием выполнено с использованием пакета MATLAB R2009b и программы SVR [4]. Иллюстрацией результатов прогнозирования служат рис. 2–4.
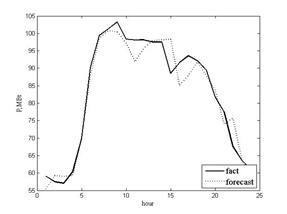
Рис. 2
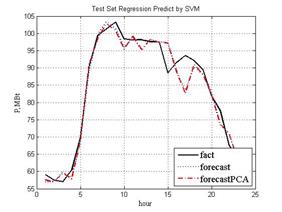
Рис. 3
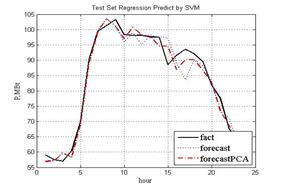
Рис. 4
Параметры ядерных функций, принятых при моделировании, и ошибки прогноза указаны в таблице.
|
Функция |
Параметры |
Ошибка прогноза, % |
|
|
s |
|
||
|
SVM (рис. 2) |
13 |
65 |
3.3451 |
|
SVM+GA(PCA), (рис. 3 ) |
9.25 |
96 |
2.99 (2.77) |
|
SVM+PSO(PCA), (рис. 4) |
6 |
55 |
2.9 (2.398) |
В результате предварительной обработки данных обучающей выборки с использованием метода главных компонентов, применения метода опорных векторов и эволюционных алгоритмов оптимизации точность прогнозирования электропотребления удалось повысить. Ошибка прогнозирования уменьшилась по сравнению с прогнозом на основе статистических моделей в 2 раза [3].
Работа выполнена при финансовой поддержке Министерства образования и науки РФ в рамках государственного задания на оказание услуг (выполнение работ), на 2012–2014 гг., шифр проекта 7.1299.2011
Рецензенты:
Микеров Александр Геннадьевич, доктор технических наук, профессор, профессор СПбГЭТУ, г. Санкт-Петербург.
Соловьева Елена Борисовна, доктор технических наук, профессор, профессор, СПбГЭТУ, г. Санкт-Петербург.
Библиографическая ссылка
Поляхов Н.Д., Приходько И.А., Ван Е. ПРОГНОЗИРОВАНИЕ ЭЛЕКТРОПОТРЕБЛЕНИЯ НА ОСНОВЕ МЕТОДА ОПОРНЫХ ВЕКТОРОВ С ИСПОЛЬЗОВАНИЕМ ЭВОЛЮЦИОННЫХ АЛГОРИТМОВ ОПТИМИЗАЦИИ // Современные проблемы науки и образования. 2013. № 2. ;URL: https://science-education.ru/ru/article/view?id=8962 (дата обращения: 15.11.2025).



