Несмотря на наблюдающийся в последнее десятилетие пик популярности нейронных сетей, обращает на себя внимание отсутствие общепринятых унифицированных технологий нейросетевого моделирования, что, по-видимому, объясняется несовершенством теоретической базы. В связи с этим многие специалисты в области нейросетевого моделирования называют свою область не только наукой, но и в какой-то степени искусством [7]. Профессионалы-разработчики нейросетевых интеллектуальных систем, приступая к решению практически каждой новой задачи, применяют весьма внушительный арсенал различных, только им известных хитростей и ноу-хау, зачастую надеясь на интуицию, а иногда и просто – на везение. В России, как и за рубежом, существуют научные школы, которые развивают и применяют на практике свои собственные варианты нейросетевых парадигм и технологий, отмечают их преимущества, часто противопоставляя другим подходам, применяемым в других школах.
Пермской научной школой искусственного интеллекта (www.PermAi.ru) [5] на протяжении последних пятнадцати лет предпринимались попытки изобретения новых принципов построения и функционирования нейронных сетей. Осваивались пропагандируемые другими научными школами нейросетевые парадигмы неклассического типа. Однако до сих пор не нашлось практически значимых задач, для решения которых неклассические нейросети оказались бы более эффективны, чем персептроны с сигмоидными активационными функциями, изобретенные в середине прошлого столетия.
У нас сложилось твердое убеждение, что, вне зависимости от применяемых нейросетевых парадигм, попытки разработки адекватной нейросетевой математической модели могут быть успешными только в том случае, если одновременно выполняются следующие условия.
1. При постановке задачи учтено достаточное количество признаков (входных параметров модели), оказывающих влияние на результат моделирования.
2. Сформировано достаточно репрезентативное множество примеров поведения предметной области (наблюдений).
3. Во множестве наблюдений не содержатся конфликтные (противоречащие друг другу) примеры.
4. Во множестве наблюдений не содержится посторонних выбросов, либо они незначительны, либо их количество мало по сравнению с общим количеством примеров.
Настоящая работа посвящена проблеме обнаружения и исключения посторонних выбросов из статистической информации, предназначенной для обучения нейронной сети.
Прежде всего, отметим, что под посторонними выбросами понимаются примеры поведения предметной области, по каким-либо причинам выпадающие из общих закономерностей этой предметной области. Другими словами – это наблюдения, не удовлетворяющие закономерностям, которым подчиняется подавляющее большинство примеров поведения исследуемой предметной области. Причинами появления посторонних выбросов могут быть: не достаточно чисто проведенный эксперимент, ошибки измерений, сбои приборов и оборудования, искажения информации при формировании множества обучающих примеров. Причиной появления посторонних выбросов может быть также влияние факторов, не учтенных при постановке задачи и не включенных в качестве входных параметров модели.
Идея предлагаемого алгоритма обнаружения выбросов основана на том факте, что если выбросов в обучающем множестве сравнительно немного и если нейронная сеть имеет сравнительно небольшое число степеней свободы (небольшое количество синаптических весов), то после применения процедуры обучения нейронная сеть на примерах, являющихся выбросами, как правило, показывает более высокую погрешность обучения, чем на примерах, не являющихся выбросами. Используя этот эмпирический факт, алгоритм обнаружения и исключения посторонних выбросов предлагается в виде блок-схемы, представленной на рис. 1.
Согласно этой блок-схеме алгоритм включает следующие пункты.
1. Разбить множество примеров поведения предметной области на обучающее (![]() ), тестирующее (
), тестирующее (![]() ) и подтверждающее (
) и подтверждающее (![]() ) в отношении 80 : 15 : 5 (%).
) в отношении 80 : 15 : 5 (%).
2. Для множества примеров ![]() , пользуясь формулами следствия теоремы Арнольда – Колмогорова – Хехт-Нильсена [7], рассчитать минимальное и максимальное количество скрытых нейронов двухслойного персептрона:
, пользуясь формулами следствия теоремы Арнольда – Колмогорова – Хехт-Нильсена [7], рассчитать минимальное и максимальное количество скрытых нейронов двухслойного персептрона:
![]() ,
,
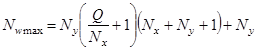 ,
,

Рис. 1. Блок-схема нейроэкспертного алгоритма последовательного обнаружения и исключения посторонних выбросов
![]() ,
,
![]() .
.
Здесь: ![]() и
и ![]() – минимальное и максимальное количество скрытых нейронов;
– минимальное и максимальное количество скрытых нейронов; ![]() и
и ![]() – минимальное и максимальное количество сил синаптических связей;
– минимальное и максимальное количество сил синаптических связей; ![]() – количество нейронов входного слоя;
– количество нейронов входного слоя; ![]() – количество нейронов выходного слоя;
– количество нейронов выходного слоя; ![]() – число элементов множества
– число элементов множества ![]() .
.
3. Рассчитать число скрытых нейронов двухслойного персептрона, предназначенного для выявления посторонних выбросов с помощью предлагаемой в настоящей статье эмпирической формулы:
![]() ,
,
в которой ![]() – эмпирический коэффициент, значение которого, в зависимости от решаемой задачи, мы рекомендуем принимать от 0 до 0,2 (рис. 2).
– эмпирический коэффициент, значение которого, в зависимости от решаемой задачи, мы рекомендуем принимать от 0 до 0,2 (рис. 2).
4. Обучить нейронную сеть на множестве ![]() и выявить пример, для которого ошибка обучения нейросети
и выявить пример, для которого ошибка обучения нейросети ![]() имеет максимальное значение.
имеет максимальное значение.
5. Предоставить информацию о выявленном примере специалисту в исследуемой предметной области и согласовать с ним вопрос о возможности удаления данного примера из множества ![]() .
.
6. В зависимости от решения эксперта: либо удалить выявленный пример из множества ![]() , либо пометить его как неподлежащий удалению, выявить следующий по величине
, либо пометить его как неподлежащий удалению, выявить следующий по величине ![]() пример и перейти на п. 5.
пример и перейти на п. 5.
7. Разбить очищенное множество ![]() на обучающее
на обучающее ![]() и тестирующее
и тестирующее ![]() в отношении 85% : 15%.
в отношении 85% : 15%.
8. Обучить и протестировать нейросеть, вычислив ошибку тестирования ![]() на множестве
на множестве ![]() . Результат тестирования изобразить графически, как на рис. 2.
. Результат тестирования изобразить графически, как на рис. 2.
9. Повторять пп. 2 – 8, пока кривая на рис. 2 не перестанет снижаться.
10. Вычислить ошибку сети ![]() на подтверждающем множестве
на подтверждающем множестве ![]() .
.
В заключение отметим, что применение предлагаемого алгоритма обнаружения и исключения посторонних выбросов в ряде случаев, при работе с сильно зашумленными статистическими данными, позволило уменьшить погрешности нейросетевых моделей в десятки раз. Особенно эффективным применение этого алгоритма оказалось при создании нейросетевого детектора лжи [2; 11; 12; 14], а также в задачах, относящихся к сфере экологии [8; 10] и медицины [9]. Менее заметное снижение погрешности – от одного до 10 процентов, зафиксировано в задачах, относящихся к сферам: экономики и бизнеса [13], политологии и социологии [15], педагогики [3], исторических наук [1], туризма [6].
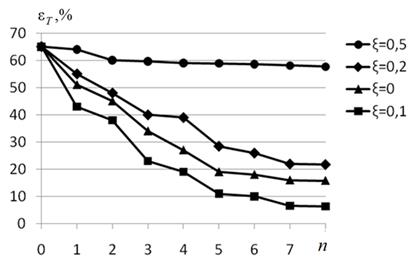
Рис. 2. Примерные зависимости погрешности тестирования ![]() от эмпирического коэффициента
от эмпирического коэффициента ![]() и от числа итераций
и от числа итераций ![]() по пп. 2-8 предлагаемого алгоритма
по пп. 2-8 предлагаемого алгоритма
Отметим также, что, в отличие от других известных алгоритмов обнаружения и исключения выбросов, например [4], предлагаемый алгоритм предполагает интерактивное участие эксперта, анализирующего правомерность удаления выявленного в качестве выброса наблюдения. Кроме того, удаление выбросов производится не за один прием, как это регламентируется алгоритмом [4], а в результате итерационного процесса строго по одному на каждой итерации.
Применение этих ноу-хау делает предлагаемый алгоритм более эффективным, позволяющим строить нейросетевые математические модели, как правило, на 1–15% более точными, чем известный алгоритм [4], преследующий аналогичные цели.
Отметим, что в нашей практике встречались случаи, как например [2; 8; 10-12; 14], когда попытки построения нейросетевых, а также регрессионных моделей, без предварительной очистки статистической информации от выбросов, осуществляемой с помощью предлагаемого алгоритма, вообще не приводили к положительным результатам, т.е. погрешности математических моделей не удавалось снизить до сколько-нибудь приемлемых для практического применения значений.
Таким образом, применение предлагаемого в настоящей работе алгоритма обнаружения и исключения посторонних выбросов из статистической информации позволяет не только повышать точность нейросетевых и регрессионных моделей, но и расширяет круг задач, для которых применение данного вида моделирования вообще возможно.
Рецензенты:
Шварц Константин Григорьевич, доктор физико-математических наук, доцент, профессор кафедры прикладной математики и информатики, Пермский государственный национальный исследовательский университет, г. Пермь.
Ясницкий Леонид Нахимович, доктор технических наук, профессор, заведующий кафедрой прикладной информатики, Пермский государственный гуманитарно-педагогический университет, г. Пермь.
Библиографическая ссылка
Сичинава З.И. НЕЙРОЭКСПЕРТНЫЙ АЛГОРИТМ ПОСЛЕДОВАТЕЛЬНОГО ОБНАРУЖЕНИЯ И ИСКЛЮЧЕНИЯ ПОСТОРОННИХ ВЫБРОСОВ ИЗ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ ПРИ ПОСТРОЕНИИ НЕЙРОСЕТЕВЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ // Современные проблемы науки и образования. 2013. № 2. ;URL: https://science-education.ru/ru/article/view?id=8903 (дата обращения: 16.11.2025).



