В современный период развития Высшего профессионального образования большое значение придаётся профессиональной направленности обучения. По мнению Г. И. Худяковой, «принцип профессиональной направленности в вузе разрешает противоречие между теоретическим характером изучаемых дисциплин и практическим умением применять эти знания в профессиональной деятельности» [5]. Особенно это значимо для студентов гуманитарных специальностей, так как профессиональная направленность является «основой мотивации и гуманизации обучения студентов будущей профессии» [5].
С целью усиления профессиональной направленности обучения математике для студентов филологических специальностей профилей подготовки «Иностранный язык», «Русский язык», «Литература», реализуемых в рамках общего направления подготовки 050100.62 «Педагогическое образование» стандартами нового поколения, вместо привычной дисциплины «математика», «математика и информатика» введена дисциплина «Основы математической обработки информации».
Пути решения задачи усиления профессиональной направленности подсказывают трактовки понятия «профессиональная направленность обучения» Г. И. Худяковой, М. И. Зайкина, С. В. Щербатых. Они выделяют содержательный и процессуальный аспекты решения данной задачи.
Содержательный аспект проявляется в насыщении курса профессионально значимым содержанием – сведениями о теоретических основах решения профессиональных задач. В настоящее время ему уделяется наиболее пристальное внимание. Проведенный нами анализ трудов отечественных и зарубежных лингвистов и математиков, таких как И. А. Бодуэн де Куртенэ, М. Н. Петерсон, В. В. Виноградов, Р. Г. Пиотровский, А. В. Гладкий, В. А. Звегинцев, М. В. Панов, Н. Ф. Алефиренко, Б. Н. Головин и других, показал, что решение проблемы усиления профессиональной направленности математического образования студентов-филологов видится в увеличении доли теории вероятностей и математической статистики в структуре курса, а также включении в его содержание стохастических методов математической лингвистики: стилостатистики, глоттохронологии, статистических методов в лексикографии и других.
Менее разработанным, но не менее важным является процессуальный аспект усиления профессиональной направленности. Он связан с созданием комплекса методических средств, систематическое применение которых способствует формированию у студентов опыта использования научных знаний в профессиональной деятельности. Мы предлагаем формировать этот опыт путем организации поэтапного перехода от обучения решению учебных стохастических задач к профессионально-ориентированным, а от них и к профессиональным лингвистическим стохастическим задачам. Для понимания различий между этими видами задач необходимо дать характеристику различий видов деятельности, которую они определяют.
Таблица 1
Характеристика различий видов деятельности
|
Виды деятельности обучающихся в системе ВПО (А. Вербицкий) |
Виды лингвистических стохастических задач |
Характеристика видов лингвистических стохастических задач |
Место в структуре курса |
|
Учебная деятельность академического типа |
Учебные стохастические задачи |
Задачи на применение теоретических положений ТВ и МС на типичных моделях лингвистических опытов со случайным исходом |
Лекционные, практические занятия |
|
Квазипрофес-сиональная |
Профессионально-ориентированные стохастические задачи |
Сюжетно построенные лингвистические стохастические задачи, сюжет которых вводит в профессиональную ситуацию постановки таких задач |
Практические занятия, подготовительный этап лабораторных работ |
|
Учебно-профессиональная |
Профессиональные стохастические задачи |
Задачи, которые реально возникли или могли бы возникнуть в процессе лингвистического исследования и решение которых требует обращения к стохастическим методам |
Лабораторные занятия, научно-исследовательская практика, курсовые работы, выпускные квалификационные работы |
Для содержательной иллюстрации различий задач, представленных в таблице, рассмотрим конкретные примеры.
Пример 1 (учебная лингвистическая стохастическая задача)
Лингвистами установлено, что «статистическая вероятность появления глагола в произведениях Л. Н. Толстого равна 0,21, в произведениях А.И. Куприна – 0,15» [2]. Из текста каждого автора случайным образом выбирают по одному слову. Составить закон распределения случайной величины X – «Количество глаголов в выборке» и определить среднее квадратическое отклонение σ(Х) случайной величины Х. Для данной случайной величины найти функцию распределения F(x) и построить её график.
Приведенный пример показывает, что сюжетная составляющая такой задачи выполняет лишь мотивационную функцию, показывая студентам применимость изучаемой теории в лингвистике. Описание ситуации применения теории и требований здесь представлено уже с использованием всей необходимой стохастической терминологии, поэтому успешность решения задачи зависит лишь от наличия знаний соответствующей математической теории. Такие задачи могут быть использованы на лекциях для демонстрации типичных ситуаций применения введенной теории или на практических занятиях для формирования навыков ее применения.
Пример 2 (профессионально-ориентированная лингвистическая стохастическая задача)
«Для расчёта памяти автомата, распознающего устную речь, и построения алгоритма его работы приходится вычислять вероятность совпадения хотя бы одной из словоформ обрабатываемого текста с соответствующей лексемой, заданной в словаре автомата. Выбрано два одинаковых по объёму отрывка текста, из каждого отрывка случайным образом выбирается слово. Нужно определить вероятность того, что хотя бы одно из двух выбранных слов будет местоимением он» [4].
Этой задаче присущи черты как учебной, так и профессиональной задачи. В сюжетной составляющей на языке учебной информации описываются условия и содержание реального производственного процесса. Успех решения будет зависеть не только от знания теоретических положений теории вероятностей, но и от выбора вероятностной модели, которая будет использована. Задачи такого вида могут быть предложены студентам для решения на практических занятиях, а также в качестве подготовительных, на лабораторных работах.
Пример 3 (профессиональная лингвистическая задача)
Установить специфичность описанного в труде Б. Н. Головина «Язык и статистика» [2] факта существования отрицательной корреляционной зависимости между количеством существительных и количеством местоимений в русских литературных текстах для а) художественных текстов; б) для публицистических текстов. Задача данного вида уже возникала в реальном профессионально-лингвистическом исследовании. Подтверждая результаты этого исследования, студенты фактически осуществляют профессиональную деятельность. Для успешности этой деятельности необходимо использовать знания, полученные при решении учебных и профессионально-ориентированных задач. По словам А. А. Вербицкого, студенты «остаются в позиции обучающихся и в то же время по целям, содержанию, формам, процессу и требованиям к получаемым результатам в позиции специалистов» [5]. Профессиональные лингвистические задачи обычно решаются студентами на лабораторных работах, а также при выполнении курсовых и дипломных работ.
Так как процесс решения профессиональных стохастических задач является длительным и многогранным, то для проведения учебных занятий (лабораторных работ) мы решили использовать так называемую «сквозную» задачу лингвистического анализа, т.е. задачу статистического анализа одной базы данных лингвистического эксперимента, в решении которой студент продвигается на протяжении целой серии учебных занятий. Такую базу данных студенты формируют самостоятельно на этапе подготовки к лабораторным работам. Для этого им предлагается, например, выполнить следующее домашнее задание:
«Выбрать по 20 фрагментов в 100 словоупотреблениях из двух произведений различных периодов творчества любимого писателя: 1 – ранний период, 2 – поздний период. Подсчитать количество глагольных форм в каждом фрагменте. Занести полученные данные в электронную таблицу SPSS (форма такой таблицы может быть предложена студентам в готовом виде)».
Характер продвижения в решении сквозной задачи при проведении серии лабораторных работ представлен таблицей 2.
Таблица 2
Лабораторные работы для студентов-филологов со «сквозной задачей»
|
Тема лабораторной работы |
Профессиональная подзадача |
|
Первичная обработка лингвистической информации. Описательные статистики выборки |
По лингвистической выборке построить статистический ряд, получить геометрическую интерпретацию полученного статистического распределения. Определить числовые характеристики выборки. Проверить результаты в пакете анализа данных SPSS |
|
Проверка гипотезы о нормальности распределения генеральной лингвистической совокупности |
Сформировать статистические гипотезы о виде распределения генеральной лингвистической совокупности и проверить их с помощью различных критериев согласия используя программу SPSS |
|
Оценка параметров нормально распределённой лингвистической случайной величины по выборке. Определение достаточного объёма выборки в лингвистических исследованиях |
Построить доверительные интервалы для параметров нормально распределённой лингвистической величины, найти ошибки измерения. Определить достаточный объём выборки по заданной возможной ошибке. Произвести проверку в SPSS |
|
Проверка гипотезы о статистической значимости различия средних двух независимых лингвистических совокупностей |
Cформулировать гипотезы о параметрах распределения лингвистической информации. Проверить гипотезы, используя параметрические критерии. Проверить результаты в программе SPSS |
|
Корреляционный анализ. Проверка гипотезы о статистической зависимости двух лингвистических совокупностей |
Оценить величину корреляционной зависимости лингвистических величин с помощью коэффициента корреляции Пирсона. Построить простую линейную регрессию по экспериментальным данным, используя программу SPSS |
|
Однофакторный дисперсионный анализ. Исследование влияния фактора на лингвистическую СВ |
Проверить влияние независимой СВ (номинативный признак) на зависимую лингвистическую СВ, измеренную в метрической шкале. Применить при проверке однофакторный дисперсионный анализ. Использовать программу SPSS |
Еще одной особенностью решения задачи профессиональной направленности обучения математике в процессуальном аспекте является обучение использованию программных продуктов специального назначения для обработки и анализа статистических данных. Для обработки лингвистической информации на компьютере мы выбрали пакет анализа данных SPSS Statistics. Данная программа проста в употреблении, универсальна, не требует от студентов знания математических формул, владения техникой вычислений, поэтому наиболее удобна для студентов-гуманитариев.
Для демонстрации специфики постановки профессиональных стохастических лингвистических задач на лабораторных работах рассмотрим задачу на проверку влияния периода творчества автора на частоту употребления глагольных форм. Эта задача решается методом однофакторного дисперсионного анализа. Так как фактор имеет только две градации, то вместо дисперсионного анализа можно использовать критерий t-Стьюдента для сравнения средних двух независимых выборок. В случае если выборки имеют различные объёмы и при проверке равенства дисперсий будет получен отрицательный результат, то может быть использован наиболее чувствительный аналог критерия Стьюдента для независимых выборок – критерий U-Манна – Уитни.
Пример 4. Лабораторная работа на тему «Исследование влияния периода творчества автора на частоту употребления глагольных форм»
Цель работы: научиться применять однофакторный дисперсионный анализ для проверки влияния независимой СВ (номинативный признак – фактор) на зависимую лингвистическую СВ, измеренную в метрической шкале (результативный признак).
Постановка задачи. В лингвистике часто требуется проверить влияние на нормально распределённую лингвистическую случайную величину определённого фактора, имеющего несколько уровней (градаций), например, исследовать влияние на распределение частоты употребления в художественных текстах, относящихся к различным периодам творчества автора одних и тех же словоформ.
Используя программу SPSS и составленную при выполнении подготовительного домашнего задания базу данных об употреблениях глагольных форм в текстах любимого писателя в разные периоды его творчества, проверить на уровне значимости р=0,05 гипотезу о зависимости числа употребления (средней частоты) глагольных форм от периода написания произведения. Для решения задачи используйте результат лабораторной работы № 2 (доказано на уровне значимости р=0,05, что случайная величина Y – «число употребления глагольных форм», имеет нормальное распределение). Предварительно докажите возможность использования для решения задачи дисперсионного однофакторного анализа (проверьте гипотезу об однородности дисперсий).
План решения задачи вручную
1) Сформировать нулевую Н0 и альтернативную Н1 гипотезы однофакторного дисперсионного анализа.
2) Найти общее среднее![]() и групповые средние значения:
и групповые средние значения: ![]() .
.
3) Вычислить суммы квадратов отклонений значений выборки от среднего:
![]() ;
; ![]() ;
; ![]()
4) Определить число степеней свободы: для общей суммы квадратов ![]() ; для межгрупповой –
; для межгрупповой – ![]() ; для внутригрупповой –
; для внутригрупповой – ![]() , где n – число всех значений выборки (для нашей задачи n=15), k – число групп (m=2).
, где n – число всех значений выборки (для нашей задачи n=15), k – число групп (m=2).
5) Найти средние квадраты отклонений: 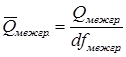 ;
; 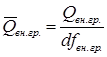 .
.
6) Вычислить эмпирическое F-отношение: 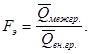
7) По таблице критических значений F-распределения для направленных альтернатив (распределение Фишера – Снедекора) найти критическое значение ![]() с найденным числом степеней свободы числителя
с найденным числом степеней свободы числителя ![]() и числом степеней свободы знаменателя
и числом степеней свободы знаменателя ![]() .
.
8) Сделать вывод относительно принятия или опровержения гипотез Н0 и Н1.: если ![]() , то гипотеза Н0 не отвергается, т. е. влияние фактора на результативный признак не доказано, если
, то гипотеза Н0 не отвергается, т. е. влияние фактора на результативный признак не доказано, если ![]() , то гипотеза Н0 отвергается с вероятностью ошибки р (уровень значимости указан в таблице), т. е. фактор существенно влияет на результативный признак Y.
, то гипотеза Н0 отвергается с вероятностью ошибки р (уровень значимости указан в таблице), т. е. фактор существенно влияет на результативный признак Y.
Для решения задачи в программе SPSS необходимо:
– открыть программу SPSS, в главном окне перейти на вкладку «переменные», ввести следующие переменные: N (номер), числовая переменная, шкала порядковая;
Y (число глаголов), числовая переменная, шкала количественная; Х (период творчества), числовая переменная, шкала номинальная. Установить метки значений переменной Х: 1 – «ранний период», 2 – «поздний период», перейти в окно «данные» и ввести исходные значения переменных;
– выбрать «Анализ»→«Сравнение средних»→«Однофакторный дисперсионный анализ»;
– перенести в окно «зависимые переменные» переменную Y, а в окно «фактор» переменную Х (период творчества);
– открыть вкладку «параметры» и отметить «описательные», «проверка однородности дисперсии» и «график средних» → «продолжить» →ОК.
Получаем: 1) описательные статистики; 2) критерий однородности дисперсии по статистике Ливиня (если уровень значимости (Знч) больше 0,05, то отличие дисперсий статистически не значимо; 3) дисперсионный анализ (если уровень значимости не превышает 0,05, то отличия средних значений в группах статистически значимо); 4) график зависимости среднего значения количества глаголов от периода творчества.
В результате решения задачи студенты получают возможность сделать следующий качественный вывод: частота употребления глаголов меняется во время творческой деятельности автора, что говорит о изменении динамичности, действенности повествования автора.
Приведенный пример показывает, что компьютерное решение профессиональной задачи концентрирует внимание студентов не на технике математических вычислений, а на условиях выбора математического метода и интерпретации результатов его применения.
Практическая апробация представленной методики формирования у студентов-филологов опыта использования стохастических методов в лингвистических исследованиях показывает, что такой подход формирует положительную мотивацию студентов к изучению математики, снижает их тревожность, связанную с успешностью овладения содержанием курса, снимает формализм результатов обучения студентов-филологов математике в вузе.
Рецензенты:
Шабанова Мария Валерьевна, доктор педагогических наук, профессор, зав. кафедрой методики преподавания математики Северного (Арктического) федерального университета имени М. В. Ломоносова, г. Архангельск.
Симашко Татьяна Васильевна, доктор филологических наук, профессор, зав. кафедрой языкознания Гуманитарного института Северодвинского филиала Северного (Арктического) федерального университета имени М. В. Ломоносова, г. Архангельск.
Библиографическая ссылка
КОКОРИНА И.В. ПРОЦЕССУАЛЬНЫЙ АСПЕКТ ПРОФЕССИОНАЛЬНОЙ НАПРАВЛЕННОСТИ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ СТУДЕНТОВ-ФИЛОЛОГОВ И ЕГО РЕАЛИЗАЦИЯ ПРИ ИЗУЧЕНИИ СТОХАСТИЧЕСКИХ МЕТОДОВ МАТЕМАТИЧЕСКОЙ ЛИНГВИСТИКИ // Современные проблемы науки и образования. 2013. № 2. ;URL: https://science-education.ru/ru/article/view?id=8862 (дата обращения: 02.07.2025).



