Реформирование системы образования в Республике Армения привело к изменению структуры обучения. При переходе на 12-летний срок обучения возникла необходимость пересмотреть содержательную и психолого-педагогическую систему нового цикла обучения.
В новых действующих программах большое место отведено обобщающему повторению курса экзаменационных дисциплин. Все второе полугодие 12-ого класса в программе предусмотрено повторение пройденного материала и организация консультаций [2].
Согласно учебному плану по физике, обучению по углубленной программе отведено 578 учебных часов (X-136 ч., XI-170 ч., XII-272 ч.), при этом для обобщающего повторения предусмотрено все II полугодие XII класса, что составляет 136 часов или около 24 % всех часов. Следовательно, в среднем на каждые 4 часа приходится один час повторения. Количество часов для неспециализированных классов составляет 306 часов (X-102 ч., XI-102 ч., XII-102 ч.). Из них 56 часов, или около 18 % всех часов, предусматривается для обобщающего повторения. В связи с этим возникла необходимость разработать продуктивную учебно-методическую систему организации повторения курса физики, так как существует явная опасность того, что вместо систематизации знаний учащихся и формирования на этой основе целостной физической картины мира отводимое на повторение школьного курса физики время будет потрачено на примитивное “натаскивание” по запоминанию необходимых для прохождения итогового тестирования формул, в результате чего будет потерян смысл обучения физике и будут отброшены декларируемые цели и задачи обучения [5].
Методологизация и повышение научного уровня школьного физического образования в настоящее время связаны с широким применением методов научного познания при обучении.
Для глубокого осознанного овладения физикой и развития физического понимания необходимо уже в средней школе строить обучение на основе последовательного использования методов научного познания. Но как показывает педагогический опыт, обучать школьников применению качественных методов физики при обучении теоретическому материалу и решении задач довольно трудно. Для этого от преподавателя требуется систематическое применение особых действий и приемов. В рамках одной или двух задач трудно объяснить школьникам суть качественных методов физики. Для полного понимания их сущности необходимо привести яркие примеры из разных разделов и тем физики, иллюстрирующие их проявления.
При обобщающем повторении курса физики возникают хорошие возможности широкого применения научных методов познания, так как при повторении возможно рассмотреть весь объем изучаемого материала курса и проводить при этом параллели между сходными понятиями и процессами, применять разнообразные качественные методы познания и использовать широкий спектр межпредметных и внутрипредметных связей. При повторении особо подчеркивается роль метода аналогии, так как в основе этого метода лежит сравнение, которое проявляется при сопоставлении объектов, процессов и явлений.
В толковом словаре русского языка аналогия представлена как “форма умозаключения, когда на основании сходства двух предметов, явлений в каком-либо отношении делается вывод об их сходстве в других отношениях”. Физическая система или явление может быть описана качественно и количественно. Такое описание физической системы будет полным, однако в некоторых случаях достаточно только качественного или количественного описания. Таким образом, физические системы или явления могут быть сходны, похожи, аналогичны как по своему поведению, так и по математическому их описанию. В большинстве случаев при обучении физике для применения метода аналогии в качестве сравниваемых объектов принимаются конкретные физические системы, и с помощью сравнений устанавливают новые отношения. Типичным примером является существующая аналогия между механическими и электрическими колебательными процессами. При расчете сложных механических систем часто прибегают к электромеханической аналогии, моделируя механическую систему соответствующей электрической. Устанавливая соответствующие характеристики механических и электрических систем, бывает возможным намного проще решать задачи и избежать сложных математических выкладок. Такими характеристиками являются масса тела и индуктивность катушки ![]() , жесткость пружины и величина, обратная электроемкости конденсатора
, жесткость пружины и величина, обратная электроемкости конденсатора ![]() , координата тела и заряд конденсатора
, координата тела и заряд конденсатора ![]() , скорость тела и сила тока контура
, скорость тела и сила тока контура ![]() , вязкость среды и активное сопротивление
, вязкость среды и активное сопротивление ![]() , внешняя сила, действующая на тело, и напряжение внешнего источника переменного тока
, внешняя сила, действующая на тело, и напряжение внешнего источника переменного тока ![]() и т.д. Опыт работы показывает, что при обучении, в частности, в процессе обобщающего повторения курса физики в средней школе эффективным оказывается применение метода аналогии, основанного на сходстве математических методов вычисления, то есть относительно математических моделей. А таких примеров в действующих учебниках много, но они не всегда явно продемонстрированы. Бывают случаи, когда при количественном описании физических явлений полученные математические выражения позволяют ввести разные физические характеристики и комментировать их физический смысл. При этом применяется следующий подход: среднее значение физической величины, меняющейся во времени, приравнивается аналогичной постоянной величине, которая определяется таким же математическим выражением, что и первое. Приведем пример: известно, что и скорость при равномерном прямолинейном движении, и средняя скорость при неравномерном прямолинейном движении определяются одинаковым математическим выражением:
и т.д. Опыт работы показывает, что при обучении, в частности, в процессе обобщающего повторения курса физики в средней школе эффективным оказывается применение метода аналогии, основанного на сходстве математических методов вычисления, то есть относительно математических моделей. А таких примеров в действующих учебниках много, но они не всегда явно продемонстрированы. Бывают случаи, когда при количественном описании физических явлений полученные математические выражения позволяют ввести разные физические характеристики и комментировать их физический смысл. При этом применяется следующий подход: среднее значение физической величины, меняющейся во времени, приравнивается аналогичной постоянной величине, которая определяется таким же математическим выражением, что и первое. Приведем пример: известно, что и скорость при равномерном прямолинейном движении, и средняя скорость при неравномерном прямолинейном движении определяются одинаковым математическим выражением: ![]() и
и ![]() . Последнее позволяет выяснить физический смысл средней скорости, а именно, средняя скорость при неравномерном прямолинейном движении равна скорости такого равномерного прямолинейного движения, при котором движущееся тело совершает одинаковое перемещение
. Последнее позволяет выяснить физический смысл средней скорости, а именно, средняя скорость при неравномерном прямолинейном движении равна скорости такого равномерного прямолинейного движения, при котором движущееся тело совершает одинаковое перемещение ![]() за одинаковое время
за одинаковое время ![]() . Здесь имеем дело с аналогией, в основе которой лежит одно и то же математическое моделирование, а именно, отношение
. Здесь имеем дело с аналогией, в основе которой лежит одно и то же математическое моделирование, а именно, отношение ![]() . Последнее позволяет выяснить смысл средней скорости неравномерного движения. Из курса физики приведем еще один подобный пример. При изучении переменного синусоидального тока вводится понятие действующей силы переменного тока, и получается выражение для расчета выделяемой теплоты:
. Последнее позволяет выяснить смысл средней скорости неравномерного движения. Из курса физики приведем еще один подобный пример. При изучении переменного синусоидального тока вводится понятие действующей силы переменного тока, и получается выражение для расчета выделяемой теплоты: ![]() , которое имеет сходство с выражением закона Джоуля – Ленца для постоянного тока:
, которое имеет сходство с выражением закона Джоуля – Ленца для постоянного тока: ![]() . Здесь также аналогия основана на сходстве математических выражений, которые позволяют сделать заключения относительно сходств других характеристик, а именно, действующей силы переменного тока
. Здесь также аналогия основана на сходстве математических выражений, которые позволяют сделать заключения относительно сходств других характеристик, а именно, действующей силы переменного тока ![]() . Это пример аналогии, действующей в рамках одного и того же явления, и суть его – выявление и объяснение сходных величин на основе сходных математических формул.
. Это пример аналогии, действующей в рамках одного и того же явления, и суть его – выявление и объяснение сходных величин на основе сходных математических формул.
Для наглядности и экономии времени, как показывает опыт, целесообразно представить сопоставляемые модели в виде таблиц. Пример аналогии характеристик и соответствующих математических формул гравитационного и электростатического полей представим в виде таблицы (таб. 1) [4].
Основные характеристики и формулы гравитационного и электростатического полей
|
Вид взаимодействия |
Теория, объясняющая взаимодействие |
Вид поля |
Характер поля |
Формула, определяющая взаимодействие |
Характеристики поля |
Принцип суперпозиции полей |
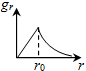
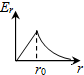
График |
|
|
силовая |
энергетическая |
|||||||
|
Гравитационное |
Близкодействие |
Гравитационное |
Потенциальное |
|
|
|
|
|
|
Электростатическое |
Близкодействие |
Электростатическое |
Потенциальное |
|
|
|
|
|
Потенциальный характер этих полей и сходство основных формул позволяют установить сходные величины: ![]() и т.д. Существование такого сходства помогает сразу определить работу, совершаемую электростатическим полем неподвижного точечного заряда
и т.д. Существование такого сходства помогает сразу определить работу, совершаемую электростатическим полем неподвижного точечного заряда ![]() при перемещении точечного заряда
при перемещении точечного заряда ![]() , находящегося на расстоянии
, находящегося на расстоянии ![]() от заряда
от заряда ![]() , на расстояние
, на расстояние ![]() , зная выражение для работы, совершаемой гравитационным полем Земли при перемещении тела с массой
, зная выражение для работы, совершаемой гравитационным полем Земли при перемещении тела с массой ![]() из точки
из точки ![]() в
в ![]()
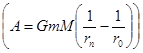 [3].
[3].
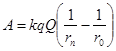 (1)
(1)
Приведем другой пример, который отчетливо демонстрирует роль аналогии при обучении теоретическому материалу и обобщающем повторении.
При изучении прямолинейного равномерного движения, когда строится график ![]() , обращают внимание на то обстоятельство, что площадь полученного прямоугольника, находящегося под графиком, численно равна пути движения тела. Далее это подтверждение распространяется на характер любого движения. В дальнейшем по аналогии этот математический метод вычисления применяется при расчетах величин, представляющих собой произведение двух взаимосвязанных других величин, например, работы силы
, обращают внимание на то обстоятельство, что площадь полученного прямоугольника, находящегося под графиком, численно равна пути движения тела. Далее это подтверждение распространяется на характер любого движения. В дальнейшем по аналогии этот математический метод вычисления применяется при расчетах величин, представляющих собой произведение двух взаимосвязанных других величин, например, работы силы ![]()
![]() , изменения импульса
, изменения импульса ![]()
![]() , количества заряда
, количества заряда ![]()
![]() и т.д. Тогда интересующая нас величина численно равна площади той фигуры, которая находится под графиком, определяющим соответственно зависимость
и т.д. Тогда интересующая нас величина численно равна площади той фигуры, которая находится под графиком, определяющим соответственно зависимость ![]() ,
, ![]() и
и ![]() .
.
В дальнейшем на основе сходства вышеуказанных математических соотношений учащиеся смогут определить и другие физические величины.
Рассмотрим задачу, в которой легко определяется физическая величина при использовании данного подхода.
Задача
Покажите, что минимальная работа по зарядке первоначально незаряженного конденсатора равна ![]() . Здесь
. Здесь ![]() и
и ![]() – окончательные заряд конденсатора и напряжение между его пластинами [1].
– окончательные заряд конденсатора и напряжение между его пластинами [1].
На рисунке 1 изображен график зависимости напряжения на конденсаторе от величины его заряда. В соответствии с определением электрической емкости,
![]() .
.
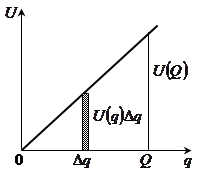
Рис.1. График зависимости напряжения на конденсаторе от величины его заряда
![]() – элементарное изменение заряда,
– элементарное изменение заряда, ![]() – значение напряжения при значении заряда конденсатора
– значение напряжения при значении заряда конденсатора ![]() ,
, ![]() – плошадь заштрихованной фигуры.
– плошадь заштрихованной фигуры.
Из графика видно, что величина ![]() , численно равная работе внешней силы по переносу единичного положительного заряда с отрицательно заряженной пластины конденсатора на положительно заряженную, тем больше, чем больше заряд
, численно равная работе внешней силы по переносу единичного положительного заряда с отрицательно заряженной пластины конденсатора на положительно заряженную, тем больше, чем больше заряд ![]() конденсатора. Работа по дополнительной зарядке конденсатора от заряда
конденсатора. Работа по дополнительной зарядке конденсатора от заряда ![]() до
до ![]() равна
равна ![]() – на рисунке 1 площадь соответствующего прямоугольника выделена. Наконец, работа по зарядке конденсатора от
– на рисунке 1 площадь соответствующего прямоугольника выделена. Наконец, работа по зарядке конденсатора от ![]() до
до ![]() может быть найдена как сумма произведений
может быть найдена как сумма произведений ![]() , т.е. как площадь прямоугольного треугольника с катетами
, т.е. как площадь прямоугольного треугольника с катетами ![]() и
и ![]() :
:
![]() .
.
Таким образом, при повторении метод аналогии позволяет учащимся не только более глубоко понять известные физические явления, понятия и процессы, но и выработать умения и навыки находить, вычислять и объяснять физические характеристики и величины на основе сходства применяемых математических моделей.
Рецензенты:
Дрмеян Генрик Рубенович, доктор физико-математических наук, профессор, зав. кафедрой физики Гюмрийского государственного педагогического института им. М. Налбандяна, г. Гюмри.
Согоян Спартак Сергеевич, доктор педагогических наук, проректор Гюмрийского государственного педагогического института им. М. Налбандяна, г. Гюмри.
Библиографическая ссылка
Цатурян А.М., Цатурян А.М. ПРОЯВЛЕНИЕ МЕТОДА АНАЛОГИИ ОТНОСИТЕЛЬНО МАТЕМАТИЧЕСКИХ МЕТОДОВ ВЫЧИСЛЕНИЯ В ПРОЦЕССЕ ОБОБЩАЮЩЕГО ПОВТОРЕНИЯ КУРСА ФИЗИКИ В СРЕДНЕЙ ШКОЛЕ // Современные проблемы науки и образования. – 2013. – № 2. ;URL: https://science-education.ru/ru/article/view?id=8582 (дата обращения: 27.04.2024).