Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Имас О.Н. 1

---

1 Томский политехнический университет

В статье обсуждаются особенности обучения иностранных студентов предмету «математика», связанные с лингвистическими трудностями использования русского языка в математике. Анализируются лингвистические предметные компетенции выпускников предвузовского курса. Формулируются цели дисциплины «математика», связанные не только с предметом, но и с языковыми целями. Проводится анализ возможностей использования языковых знаний студентами в процессе презентации математических задач. Приводятся типичные ошибки аудирования при изучении терминов. Обсуждаются особенности языка математики и его место в научном стиле речи иностранных студентов. Обсуждаются методические приемы совмещения предметных целей дисциплины и развития лингвистических навыков студентов. Предлагаются коррекционные мероприятия для усовершенствования языковых навыков иностранных студентов на всех ранних этапах обучения: предвуз, первый и второй семестры первого курса. Анализируются недостатки лингвистической методической базы преподавателей-предметников.

Статья в формате PDF

94 KB

иностранные студенты

лингвистическая конструкция

язык математики

термин

конспектирование

диктант

1. Ильченко А.Н., Солон Б.Я. Математическая культура — основа профессиональной подготовки специалиста для инновационной экономики // Современные проблемы науки и образования. – 2010. – № 2. – С. 119-129.

2. Кийкова Н.Ю. Синергетические основания модели математической культуры будущего менеджера // Фундаментальные исследования. – 2012. – №3. – С. 38-43.

3. Кашкан Г.В., Провалова Н.В., Шахова Н.Б. Реализация межпредметных связей при обучении иностранных граждан // Современные проблемы науки и образования. – 2011. – № 6; URL: www.science-education.ru/100-5073

4. Пасаита Т.Н. Обучение конспектированию иностранных учащихся на занятиях по языку специальности // Proceedings of the VII International Conference “International Cooperation in Engineering Education” (St. Petersburg, Russia, 2-4 July 2012). – St. Petersburg, 2012. – p. 85-92.

5. Сурыгин А. И. Педагогическое проектирование системы предвузовской подготовки иностранных студентов. – СПб.: Златоуст, 2001. – С. 73-77.

Интернационализация и падение границ на рынке образовательных услуг открывают широкие возможности, как для студентов, так и для преподавателей для включения в единый общемировой процесс продвижения и совершенствования образовательной деятельности. Для иностранных студентов, избравших российский университет, прежде всего, возникает необходимость овладения языком страны пребывания. Как правило, российские вузы уже давно участвуют в международном образовательном процессе, имеют достаточно практического и теоретического опыта и успешно осуществляют языковую подготовку будущих студентов на предвузовском этапе. Дальнейшее обучение иностранных студентов, как правило, происходит в общих потоках русскоговорящих студентов и является весьма не простым для них в силу многих причин, в том числе и языковых. Томский политехнический университет (ТПУ) пошел по пути организации отделения неполного высшего образования, где иностранные студенты обучаются в течение первых двух-трех семестров отдельно от русскоговорящих студентов. Это позволяет преподавателям сконцентрировать внимание на обеспечении не только предметных умений и навыков студентов, но и на формировании лексической и терминологической базы, необходимой им при обучении на последующих курсах в русскоязычных потоках.

В данной статье анализируются лингвистические предметные компетенции выпускников предвузовского курса, дальнейшее развитие умений и навыков студентов в рамках аудиторных занятий и самостоятельной работы по дисциплине «математика» и языковые проблемы, возникающие у иностранных студентов при изучении данного предмета.

На этапе предвуза основной задачей любого университета [4] является развитие умений и навыков, которые позволили бы студенту учиться на первом курсе: читать научную и учебную литературу, слушать лекции, говорить и участвовать в работе практических и семинарских занятий. Действительно, как показывает повседневная работа с иностранными студентами первого курса на занятиях по дисциплине «математика», студенты ТПУ, прошедшие предвузовскую подготовку вполне удовлетворительно излагают свои мысли, читают и понимают прочитанные задания, комментируют решение задач и доказательства. Однако, лекционные занятия остаются для них наиболее трудной формой работы: студенты плохо понимают звучащий текст, не успевают записывать словесные формулировки даже вслед за преподавателем (в то время как математические выкладки они записывают наравне с русскоговорящими студентами), с трудом перефразируют символьный математический язык в правильные с точки зрения русского языка предложения. Огромные трудности при запоминании и использовании вызывает предлагаемый классический, принятый в математике, вариант формулировок определений. Поэтому, основными задачами второго этапа обучения – в рамках отделения неполного высшего образования – является, во-первых, развитие навыков владения русским языком как средством познания, коммуникации, средством презентации и анализа, то есть на уровне, приближенном к уровню носителей языка; во-вторых, изучение базовых разделов математики, с которых традиционно начинается освоение любой образовательной программы. Решение этих задач необходимо для успешного освоения программы профессиональных курсов иностранным студентом и его безболезненной адаптации в русскоговорящих группах. Это накладывает на преподавателей дополнительные задачи: преподаватель-предметник должен обладать лингвометодической компетентностью [5].

Важной компонентой при формировании коммуникативной компетенции иностранных студентов для общения в учебно-профессиональной сфере является владение определенным объемом математической терминологии и частотными лексико-грамматическими конструкциям, характерными для языка математики. С этой целью для иностранных студентов было подготовлено пособие, разработаны наглядные интерактивные материалы, используемые в лекционных занятиях с выделенными терминами, которые студенты должны запомнить и включить в свою активную лексику. Проблема овладения научным стилем речи заключается еще и в том, что данным видом лексики студент пользуется только в рамках своей учебной деятельности, причем, преимущественно в рамках аудиторной работы. Поэтому почти половина времени аудиторных занятиях первого семестра первого курса посвящена «говорению» на математические темы. Тем не менее, несмотря на предварительную работу с термином (разбор определения, работа с примерами, домашние задания на изучение терминов), 20% студентов «не слышат» термин даже в контексте предложения, в то время как использование термина в контексте задачи, которую они читают, не вызывает затруднений. В таблице 1 приведены наиболее часто встречающиеся ошибки аудирования.

Таблица 1

Следует отметить, что двух диктантов с использованием одних и тех же терминов бывает достаточно, чтобы ошибки прекратились. Однако огорчает, что записывая предложения под диктовку, студенты не анализируют свой результат, хотя, встречая опечатки в текстах задач, замечают их. Кроме того, для иностранных студентов традиционно остаются трудными правильное употребление падежей и времен, реже – склонения глаголов.

Совместный со студентами анализ сделанных ошибок показал, что неправильно услышанный и написанный ими термин они понимают и определяют правильно: произведение – это умножение, производная – это предел отношения соответствующих приращений… и др. То есть, находясь в условиях работы над данной темой, подобные описки не страшны, они быстро корректируются. Опасность заключается в лекционном конспектировании, когда неправильно услышанный и записанный текст приходится использовать для подготовки к экзамену или зачету. В этом случае вся проделанная работа и преподавателем и студентам становится бесполезной – студент не может использовать свой конспект и обращается к учебникам, что в свою очередь значительно усложняет подготовку: студент сталкивается с лавинообразным потоком знакомых ему слов, употребляемых в непонятном смысле – математических конструкциях; в учебнике, в отличие от лекции, не акцентируются «жизненно необходимые» понятия и теоремы, в результате студенту-иностранцу приходится изучать все «от корки до корки». Следует отметить, что для математики такая ситуация не критична. Математика, в силу своей наднациональной специфики, как неоднократно отмечалось в литературе [1-2], практически в любом учебнике имеет одинаковую структуру и логику изложения. Иностранные студенты пользуются этим, и практически все имеют учебники высшей математики на своем родном языке. К завершению изучения трехсеместрового курса высшей математики, средний иностранный студент достигает целей дисциплины: овладевает ее идеальными понятиями и абстрактными структурами, методами доказательств и обоснования решений, вычислительным аппаратом. Нашей же целью, кроме предметных, является использование математики как дисциплины вне рас и культур для совершенствования русского языка иностранных студентов до уровня максимально приближенного к уровню носителей языка.

Другой проблемой владения языком является отсутствие свободы изложения своих мыслей, привязанность к заученным терминологическим грамматическим конструкциям. Так, комментируя доказательство с достаточно громоздкими выкладками, например:

,

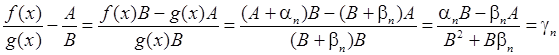студенты тщательно прочитывают все математические действия, собственно, как их и научили в курсе довузовской подготовки. Выглядит это так:

«рассмотрим: функция f от x разделить на функцию g от x, минус A

разделить на B, равно функция f от x умножить на B минус функция

g от x умножить на A разделить на функцию g от x умножить на B…»

и т.д. И это прочитано только два выражения! Но от первокурсника требуется не чтение формулы, а идея выполняемого действия. В идеале студент должен прочитать записанное выражение следующим образом:

«рассмотрим разность между отношением функций f к g

и отношением их пределов A к B. Приведем к общему

знаменателю. По свойству предела заменим функции f и g на

соответствующие суммы А плюс бесконечно малое a и B плюс

бесконечно малое b. Раскроем скобки и упростим выражение…»

и т.д. В данном прочтении осталось лишь сделать математический вывод, а вся формула уже произнесена. Возвращаясь к рекомендованному прочтению формулы, отметим, что мы намеренно прочитали «суммы А плюс бесконечно малое a» вместо «суммы А и бесконечно малое a» напоминая тем самым свойство, на которое необходимо сделать ссылку при комментировании выражения. Подобные отклонения от правил также являются для студентов «приглашением» к заучиванию новой конструкции, которая впоследствии потребует пояснений, где она будет употребляться.

Решение данной проблемы с одной стороны достаточно просто: необходимо включить изучение подобных устойчивых математических конструкций либо на уровне предвуза, либо в курсе русского языка. С другой стороны математика изобилует огромным количеством своеобразных конструкций. Каждую из них иностранцам придется заучивать как новое выражение, нигде более не используемое, как в языке математики. Кроме того, подобную проблему можно решать, используя межпредметные связи [3], например, инженерную графику или физику, вычленяя общие лексические конструкции и используя их в качестве центров кристаллизации для наращивания и активирования терминологического запаса. 

Таким образом, в результате интенсивной работы с иностранными студентами первого курса можно сделать вывод, что студенты, прошедшие предвузовскую подготовку удовлетворительно излагают свои мысли, хорошо читают, в основном понимают прочитанные задания, хорошо справляются с заданиями входного предметного тестирования. В то же время, студенты не умеют конспектировать, плохо «слышат» и понимают услышанное, предпочитают использовать длинные, но отработанные грамматические конструкции вместо коротких, но емких по смыслу, выражений. В связи с этим, преподаватели отделения неполного высшего образования видят свою задачу не только в формировании предметных компетенций иностранных студентов, но и в развитии их лексических навыках и умениях. Однако, для этого было бы полезным, например, в рамках повышения их квалификации, организовать обучение преподавателей-предметников особенностям преподавания научного стиля речи для иностранных студентов, а так же предоставить возможность изучить основные методики обучения русскому языку как иностранному.

Рецензенты:

Килин Виктор Андреевич, д.ф.-м.н., профессор кафедры Высшей математики ФГБОУ ВПО «Национальный исследовательский Томский государственный университет», г. Томск.

Лукьянова Наталия Александровна, д.ф.н., профессор, зав. кафедрой социологии, психологии и права ФГБОУ ВПО Национальный исследовательский Томский политехнический университет, г. Томск.

Библиографическая ссылка