Известен ряд случаев, когда относительно слабое землетрясение инициировало движение больших подводных оползней, которые действуя как поршень, приводят к генерации морских волн (см., например,[8]). В ряде работ разработаны аналитические теории генерации волн цунами движущимися подводными оползнями (соответствующие ссылки можно найти в [2]). Однако во всех этих работах предполагалась, что характеристики оползня не меняются со временем. Между тем, как следует из результатов численного моделирования, динамика самого подводного оползня является достаточно сложной [8].
Следует отметить, что оползни бывают не только подводными. Известны многочисленные случаи схода оползней и лавин со склонов гор, приводящие к многочисленным жертвам. Отметим и региональный характер оползневой опасности для Нижегородской области. Так, еще в 1597 году Печерский монастырь сошел в реку Волга в районе Нижнего Новгорода. Вот как кратко описано в летописи (цитируем по [1]): «В 1597 году, 18 июня, разразился над Нижним Новгородом гнев Божий: оторвавшись от матерой земли оползла гора в Печерском монастыре и с растущим на ней лесом вдвинулась в Волгу сажен на 50, а местами и более, вследствие чего на реке поднялось страшное волнение: стоявшие на воде под монастырем суда выбросило на берег сажен в 20 от воды и более». Из исторического описания можно сделать вывод, что источником оползня стало повышение уровня грунтовых вод, приведшее к разжижению грунта. При этом, оползень вызвал большие волны в Волге. Это речное цунами промоделировано в [1]. Оползневая опасность берегов Волги и Оки в районе Нижнего Новгорода высока и в настоящее время. Так, по данным Комитета охраны природы и управления природопользованием Нижегородской области, только за 2000 год в Нижнем Новгороде на участках оползневых склонов этих рек образовались три новых оползня и активизировались 33 старых. Последний значительный оползень произошел 9 ноября 2004 года в Богородском районе Нижегородской области. С высокого берега реки Ока, с высоты примерно 50 м обрушился грунт объемом около 10 тысяч кубометров. Обследование этого события показало, что оползень остановился, не доходя до воды, и не возбудил цунами. Отметим недавнюю работу [5], посвященную устойчивости склонов Горьковского водохранилища, в которой выявлены береговые участки слабой устойчивости, где возможен сход оползней.
Настоящая работа посвящена исследованию нелинейной динамики оползней, сходящих с крутых склонов в рамках двух различных моделей, аппроксимирующих поля течений в оползне. В первой модели предполагается, что поток однороден по высоте, как в идеальной жидкости. Это приближение называется моделью Саваге - Хутера [3,9]. Во втором случае предполагается параболический профиль течения по высоте, подобный течению вязкого слоя жидкости [6-7].
2. Римановы волны в модели Саваге - Хутера
Основные уравнения оползневого потока с однородной вертикальной структурой, движущегося под действием силы тяжести и Кулоновского трения (модель Саваге - Хутера) в системе координат, привязанной к топографии откоса, имеют вид
![]() ,
, ![]() (1)
(1)
где h - высота потока, u - средняя по высоте скорость потока, g - ускорение силы тяжести, q - угол наклона поверхности скольжения, m=tg(j) - коэффициент кулоновского трения, φ - динамический угол трения и α = sinθ - μsinθ. Величина φ зависит от материала оползня, в частности, для лавин, сходящих с вулканов, она оценивается в 17-350. Данные уравнения отличаются от известных уравнений мелкой воды только диссипативным членом, который для воды обычно принимается в виде квадратичного трения. В дальнейшем наклон откоса предполагается постоянным и достаточным для начала движения потока (θ > φ).
Система уравнений (1) гиперболическая с постоянными коэффициентами, поэтому многие ее решения могут быть получены стандартным путем. В частности, Римановы инварианты находятся явно
![]() , (2)
, (2)
что позволяет переписать уравнения (1) в виде
![]() ,
, ![]() . (3)
. (3)
Система уравнений типа (3) изучалась в теории волн на воде [4], где, однако, кулоновское трение не рассматривалось, и наклон дна предполагался малым. Отличается и постановка задачи: в волнах на воде начальные условия соответствуют слабо-нелинейным волнам, в то время как в гравитационных потоках нелинейность всегда сильная. Тем не менее, математическая аналогия между «водными» и «потоковыми» уравнениями позволяет опустить некоторые выкладки и привести здесь часть результатов без вывода.
Решения в виде Римановых волн уже находились в литературе [3]. Они легко переписываются для потоков с учетом кулоновского трения. Риманова волна имеет следующий вид
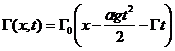 ,
, ![]() ,
, ![]() . (4)
. (4)
Это решение имеет ясный физический смысл: оползень скатывается вниз под действием редуцированной силы тяжести и укручается на фронте (рис. 1).
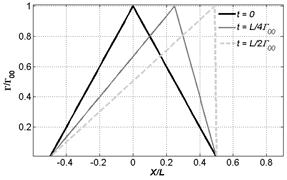
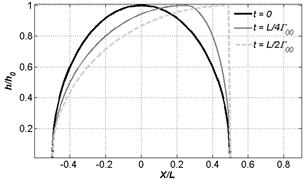
Рис. 1. Профили Римановой волны скорости (слева) и уровня (справа) в различные моменты времени, Tbr - время обрушения
За конечное время фронт оползня становится вертикальным и начинает обрушаться. Время обрушения легко находится
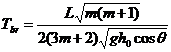 , (5)
, (5)
и оно зависит от высоты оползня и угла наклона откоса к горизонту. После обрушения это решение формально не работает, и обрушенная область должна заменяться скачком. Мы не будем, однако, вычислять амплитуду скачка, так как нашей главной целью является нахождение аналитических решений, которые для оползней с обрушенным фронтом не находятся в явном виде.
4. Римановы волны в вязкой модели оползня
В модели вязкого оползня профиль скорости по высоте не является однородным. Упрощенные уравнения такой модели для осредненного по высоте потока выведены в [6-7].
![]() , (6)
, (6)
![]() . (7)
. (7)
Эти уравнения сильно отличаются от приведенных выше уравнений модели Саваге -Хутера. В частности, скорость u является теперь скоростью частиц на поверхности оползня. Появились численные коэффициенты, которые, как мы покажем, оказывают существенное влияние на характер решения. Кроме того, сила трения зависит от скорости и высоты потока (μ = коэффициент трения).
Для поиска аналитического решения сначала пренебрежем силой трения (m = 0). Тогда уравнение (7) легко преобразовать к виду
![]() . (8)
. (8)
Вводим расход оползневого материала по поперечному сечению
![]() . (9)
. (9)
Численный коэффициент здесь возник из-за неоднородности скорости потока по высоте. Средняя скорость потока в таком течении есть 2u/3, так что выражение для расхода примет привычную форму. В результате система уравнений (6) - (8) принимает окончательный вид
![]() , (10)
, (10)
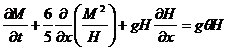 .(11)
.(11)
Эти уравнения отличаются от уравнений модели Саваге - Хутера только численным коэффициентом 6/5 вместо 1.
Примем во внимание, что в зависимости от гипотез, заложенных в теории вязкого подслоя, профиль течения может иметь более сложную форму. Поэтому мы заменим уравнение (11) на более общее
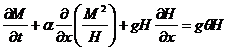 (12)
(12)
с произвольным численным коэффициентом a. Для идеальной жидкости a = 1, а для вязкого потока a = 6/5. Система (10) - (12) является гиперболической, однако Римановы волны в ее рамках еще не исследовались. В качестве первого приближения мы будем считать наклон откоса малым и пренебрежем правой частью в (12).
Для нахождения Римановых волн положим
![]() (13)
(13)
После подстановки система (10)-(12) будет представлять собой однородную линейную систему относительно первых производных от глубины. В этом случае определитель системы должен обращаться в нуль, что и ведет к обыкновенному дифференциальному уравнению для M(H)
![]() . (14)
. (14)
Удобно снова вернуться к усредненной по потоку скорости U=M/H
![]() . (15)
. (15)
Аналитические решения в случае α = 1 находятся тривиально, это случай, описанный в предыдущем параграфе. В общем же случае не удается найти решение уравнения (15) в явном виде. Для численного интегрирования удобно использовать безразмерные переменные
![]() ,
, ![]() , (16)
, (16)
где h - невозмущенная глубина потока. В результате, уравнение (15) записывается в виде
![]() . (17)
. (17)
Это уравнение должно быть решено для следующего начального условия
![]() , (18)
, (18)
означающего, что вне оползня частицы не двигаются. Поскольку уравнение (17) содержит квадрат производной, оно описывает обе волны, распространяющиеся в противоположных направлениях. Мы ограничимся анализом только одной волны и упростим уравнение (17)
![]() . (19)
. (19)
В случае идеального потока решение уравнения (19) находится в явном виде
![]() . (20)
. (20)
Для вязкого потока удается найти асимптотическое решение (19) в случае малой нелинейности (D = 1 + d, d << 1)
![]() , (21)
, (21)
следовательно, нелинейная поправка к скорости зависит от параметра a. Численное решение уравнения (19) представлено на рис. 2 (показаны решения как для прямой, так и для обратной волн). Как видим, разница между кривыми для идеального и вязкого потока незначительна, и она проявляется главным образом на нулевой глубине (на фронте потока). Однако здесь скорость вязкого потока сильно возрастает и приводит к обрушению фронта. С другой стороны, на фронте трудно ожидать стационарного параболического профиля потока, так что динамикой частиц на нулевой глубине можно пренебречь. В тоже время, если поток достаточно мощный, то скорость частиц на вершине в вязкой модели оказывается выше, чем в идеальном потоке. В этом случае нелинейная динамика возмущений в потоке будет развиваться быстрее.
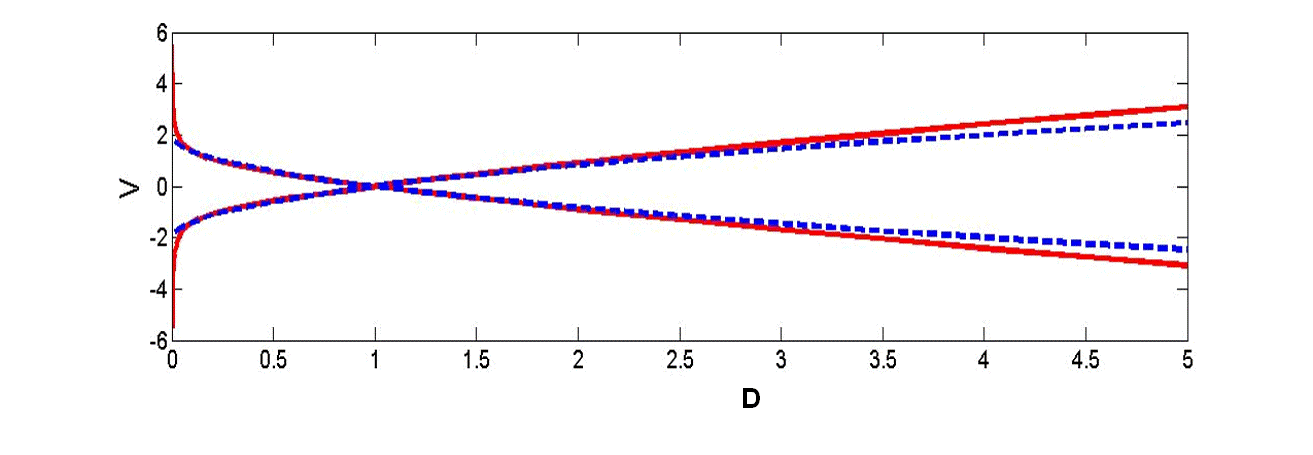
Рис. 2. Зависимость скорости частиц от высоты потока. Голубая линия соответствует идеальному потоку, красная - вязкому
Зная скорость частиц, можно получить уравнение Римановой волны из (19)-(12)
![]() , (22)
, (22)
где характеристическая скорость есть
![]() , (23)
, (23)
и
![]() . (24)
. (24)
Уравнение (23) совместно с (19) проинтегрировано численно, и характеристическая скорость показана на рис. 3. И здесь имеется особенность на фронте потока, которая не имеет физического смысла. На вершине же потока характеристическая скорость оказывается выше в вязкой модели, чем в идеальной.
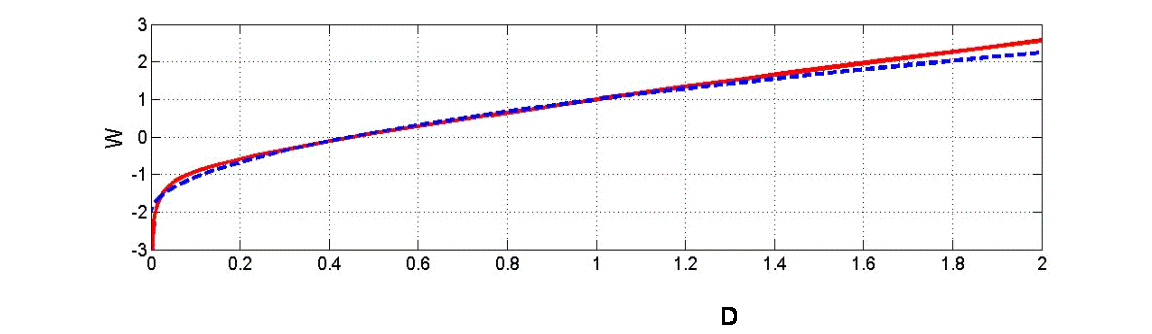
Рис. 3. Зависимость характеристической скорости от глубины потока. Голубая линия соответствует идеальному потоку, красная - вязкому.
4. Заключение
В работе получены аналитические решения уравнений движения оползней в виде Римановой волны в рамках различных моделей. Показано, что если динамика оползня описывается моделью вязкого слоя, то нелинейные эффекты развиваются быстрее на гребне оползня.
Работа выполнена при финансовой поддержке регионального гранта РФФИ № 11-05-97006.
Рецензенты:
- Галкин В.М., д.ф.-м.н., профессор, зав. кафедрой «Высшая математика» Нижегородского государственного технического университета им. Р.Е. Алексеева, г. Нижний Новгород.
- Максимов В.В., д.т.н., профессор, ФГБОУ ВПО «Санкт-Петербургский государственный университет технологии и дизайна», г. Санкт-Петербург.
Библиографическая ссылка
Петрухин Н.С., Пелиновский Е.Н., Пелиновский Е.Н. РИМАНОВЫ ВОЛНЫ В ДИНАМИКЕ ОПОЛЗНЕЙ НАД ПЛОСКИМ ОТКОСОМ // Современные проблемы науки и образования. 2011. № 6. ;URL: https://science-education.ru/ru/article/view?id=5315 (дата обращения: 02.07.2025).



