Наиболее распространенными являются устройства, содержащие аналоговые и цифровые компоненты, комбинационные схемы и элементы с памятью: они применяются практически во всех типах СЭ, где требуется реализовать специальные характеристики, обеспечить плавность и точность регулирования, повысить производительность и мощность судовых электроэнергетических систем [1,5].
Возросшие возможности мощной полупроводниковой техники, появление мощных JBT-транзисторов, способных управлять токами в сотни ампер и выдерживать напряжения до 1500 вольт, а также мощных тиристоров и семисторов, фотосемисторов и других силовых электронных приборов, использующихся в разработках современных компаний, поставляющих аппаратуру для промысловых судов, делают актуальным рассмотрение вопросов электромагнитной совместимости [5].
Проблема повышения качества судовой электроэнергии и надежности системы электропитания выдвигается на одно из первых мест.
В этой ситуации задачи прогнозирования импульсных помех от мощного судового электронного оборудования выступают на передний план, так как выход из строя мощных полупроводниковых приборов во время ведения промысла может приводить к значительным экономическим потерям, а в случае выхода из строя систем управления ответственными энергетическими процессами к потере безопасности мореплавания.
Данная работа посвящена вопросам многомасштабного анализа дискретных сигналов и прогнозированию импульсных помех.
Принципиально новым методом многомасштабного анализа является структурная индексация. Её суть заключается в выявлении структурных особенностей сигналов для последующего анализа этих особенностей.
Сигналы питающего напряжения содержат разномасштабные локальные особенности. Относительная величина и временная протяженность таких особенностей зависит от природы возмущения.
Естественным и наиболее эффективным способом представления таких сигналов является построение нелинейных адаптивных аппроксимирующих схем на основе экстраполирующих фильтров. Инструментом, позволяющим реализовать такую процедуру для сигналов с подобными особенностями, является вейвлет-преобразование.
На основе совмещения технологии вейвлет-анализа и моделей авторегрессии и проинтегрированного скользящего среднего в данной работе представлены модели сигналов питающего напряжения и проведен анализ полученных данных.
Модель, используемая при моделировании нестационарных временных рядов, называется моделью авторегрессии и проинтегрированного скользящего среднего - АРПСС или ARIMA.
В основе данной модели лежат два процесса:
1) процесс авторегрессии:
![]() ,
,
где α - константа (свободный член),
δ1, δ2 - параметры авторегрессии,
ε - случайное воздействие (ошибка);
2) процесс скользящего среднего:
![]()
где μ - константа,
θ1, θ2 - параметры скользящего среднего,
ε - случайное воздействие (ошибка).
Общий вид модели среднего значения однофакторного динамического процесса описывается следующей формулой:
![]() ,
,
где С - константа,
εt - некомпенсированный моделью случайный остаток.
В оригинальных обозначениях Бокса и Дженкинса модель ARIMA записывается как ARIMA (p, d, q),
где p - параметры авторегрессии,
d - порядок разностного оператора,
q - параметры скользящего среднего.
Для рядов с периодической сезонной компонентой применяется АРПСС с сезонностью, которая в обозначениях Бокса и Дженкинса записывается как АРПСС (p, d, q) (ps, ds, qs), где параметры во второй скобке соответственно называются «сезонная авторегрессия», «сезонная разность» и «сезонное скользящее среднее».
Аппроксимация временного ряда с помощью модели АРПСС происходит в несколько этапов.
1. Проверка ряда на стационарность. Ряд является стационарным, если он имеет постоянные по времени средние, дисперсию и автокорреляцию с удаленными сезонной, циклической и трендовой составляющей. Такой ряд называется стационарным рядом случайных остатков.
Проверить исходной ряд на стационарность можно с помощью автокорреляционной функции (АКФ) и частной автокорреляционной функции (ЧАКФ) остатков. Остатки представляют собой разности наблюдаемого временного ряда и значений, вычисленных с помощью модели.
Применение модели АРПСС предполагает обязательную стационарность исследуемого ряда. Временной ряд к стационарному виду приводят с помощью применения разностных операторов, порядок которых определяется параметром (d).
2. Идентификация порядка модели и оценивание ее параметров
На этом этапе необходимо решить, как много параметров p и q должно присутствовать в модели процесса. Основными инструментами идентификации модели АРПСС являются АКФ и ЧАКФ.
Во время оценивания порядка модели используется квазиньютоновский алгоритм максимизации правдоподобия наблюдения значений ряда по значениям параметров. Во время итераций минимизируется (условная) сумма квадратов остатков модели.
Для оценки параметров используется t-статистика Стьюдента. Если значения вычисляемой t-статистики не значимы, соответствующие параметры в большинстве случаев удаляются из модели без ущерба подгонки.
3. Прогноз. Полученные оценки параметров используются на последнем этапе для вычисления нового значения ряда и построения доверительного интервала для прогноза.
Показателем качества построенной модели АРПСС является анализ остатков. Модель АРПСС адекватно описывает исходные данные, если остатки модели являются некоррелированными, нормально распределенными случайными величинами.
Общим показателями качества построенной АРПСС модели являются критерий Акайке и байесовский критерий Шварца.
Построение модели сигнала сети
Временной ряд сложной структуры может быть представлен в виде суммы разномасштабных ортогональных компонент fj:
![]() , (1)
, (1)
![]() ,
, ![]() . (2)
. (2)
Процедуру идентификации компонент fj построим на применении методов аппроксимации, основанных на разложении функции по базису в пространстве Лебега L2R. Учитывая локальный характер анализируемых особенностей, их разномасштабность и разнообразие по форме, наиболее подходящим базисом для представления данных является вейвлет-базис:
![]()
где, ![]() - базисные вейвлет-функции пространства
- базисные вейвлет-функции пространства ![]() .
.
Вейвлет-коэффициенты ![]() рассматриваются здесь как результат отображения f в пространство с разрешением j.
рассматриваются здесь как результат отображения f в пространство с разрешением j.
Будем использовать нелинейные аппроксимирующие вейвлет-схемы. В этом случае приближение f выполняется M векторами, зависящими от структуры сигнала:
![]() ,
,
где ![]() - множество индексов, определяемое структурой сигнала f.
- множество индексов, определяемое структурой сигнала f.
Рассмотрим в качестве пространства исходных дискретных последовательностей данных пространство с разрешением j=0
![]() .
.
В этом случае нулевой уровень детальности f0 соответствует интервалу снятия показаний.
Применяя к данным конструкцию разложения в вейвлет-пакеты, получим схему разложения пространства V0:
![]() ,
,
где ![]() ;
; ![]() - пространства вейвлет-пакета.
- пространства вейвлет-пакета.
Данные с шумом будут иметь представление
![]() ,
,
где компоненты ![]()
![]() ,
, ![]() , единственным образом определяются последовательностями коэффициентов
, единственным образом определяются последовательностями коэффициентов ![]()
![]()
![]() ,
, ![]()
![]() :
: ![]() ,
, ![]() , компонента
, компонента ![]() , определяемая коэффициентами
, определяемая коэффициентами ![]() , является шумовой компонентой.
, является шумовой компонентой.
Выделенная составляющая ![]() является детализирующей компонентой и определяет локальные особенности структуры данных, сглаженная составляющая
является детализирующей компонентой и определяет локальные особенности структуры данных, сглаженная составляющая ![]() содержит устойчивые характеристики структуры.
содержит устойчивые характеристики структуры.
Компоненты ![]() и
и ![]() имеют более простую структуру, чем исходный временной ряд f, и, в силу условия (2), не коррелируют между собой. Эти свойства позволяют выполнить идентификацию моделей для каждой из полученных компонент и объединить полученные представления на основе соотношения (1) в общую модель временного ряда.
имеют более простую структуру, чем исходный временной ряд f, и, в силу условия (2), не коррелируют между собой. Эти свойства позволяют выполнить идентификацию моделей для каждой из полученных компонент и объединить полученные представления на основе соотношения (1) в общую модель временного ряда.
Численный метод идентификации компонент ![]() и f-n включает следующие операции:
и f-n включает следующие операции:
1) выбор аппроксимирующего вейвлет-базиса ![]() ;
;
2) выделение компонент ряда.
Выделенные компоненты ![]() и f-n аппроксимируются АР-моделью:
и f-n аппроксимируются АР-моделью:
Для идентификации АР-модели может быть использован итеративный подход:
- выбирается полезный класс моделей;
- получают предварительные оценки параметров модели;
- диагностические проверки позволяют выявить возможные погрешности полученной модели, если погрешности удовлетворяют требованиям, модель готова к использованию.
Этапы 1) - 3) образуют промежуточный этап общей последовательности действий по идентификации многокомпонентной модели временного ряда. При подгонке модели эти этапы должны быть выполнены для различных компонент и на основе результатов диагностических проверок полученных АР-моделей компонент должна быть идентифицирована окончательная модель, общий вид которой:
![]() ,
, ![]() (3)
(3)
где ![]() - коэффициенты авторегрессии компоненты модели масштаба j,
- коэффициенты авторегрессии компоненты модели масштаба j, ![]() ,
, ![]() ,
, ![]() - порядок АР-модели компоненты масштаба j,
- порядок АР-модели компоненты масштаба j, ![]() - оператор взятия разности назад порядка d.
- оператор взятия разности назад порядка d.
Прогнозирование значения ![]() ,
, ![]() определяет прогноз
определяет прогноз ![]() в момент
в момент ![]() с упреждением q. Значение
с упреждением q. Значение ![]() на основе полученной модели (3) можно выразить следующим образом:
на основе полученной модели (3) можно выразить следующим образом:
![]() .
.
Моделирование и прогнозирование данных сети
Для оценки эффективности предложенного метода проведены эксперименты по модельной генерации, обработке и анализу полученных модельных данных (рис. 1-2):
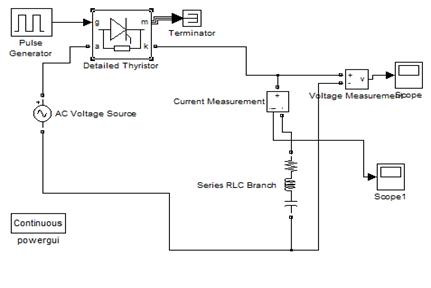
Рис.1. Модель в Simulink
Ток нагрузки изменяется по синусоидальному закону с периодом 0,02 с (рис.2,а) и определяется моделирующей функцией. Также он содержит высокочастотную составляющую, обусловленную импульсным режимом работы тиристора и относительно малой величиной индуктивной нагрузки. Эту составляющую можно наблюдать на фрагменте диаграммы (рис.2, б).
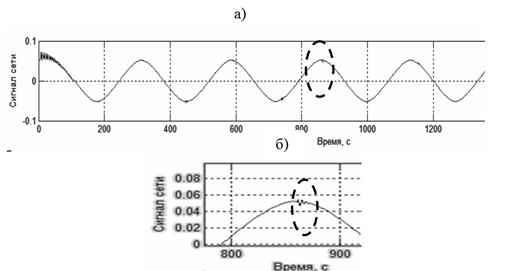
Рис.2. Модельный сигнал с импульсной помехой (а) и её фрагмент (б)
В таблице 1 приведены результаты моделирования сигналов сети.
Таблица 1. Результаты моделирования сети
|
Вид искажения |
Значение константы |
Значение 1-го параметра модели |
Значение 2-го параметра модели |
Значение 3-го параметра модели |
Значение 4-го параметра модели |
Значение 5-го параметра модели |
|
Импульсная помеха |
-0,00682 |
1,555169 |
-0,7478 |
0,782837 |
-0,54639 |
-0,04492 |
|
Восстановленный по лучшему дереву сигнал (чистый сигнал) |
-0,00046 |
1,57000 |
-0,4692 |
0,162545 |
-0,24829 |
-0,01612 |
Для импульсных помех идентифицирована АР-модель пятого порядка (рис.3):
АР: ![]() . (4)
. (4)
Для восстановленного по лучшему дереву сигналу идентифицирована АР-модель пятого порядка (рис.4):
АР: . ![]() (5)
(5)
Построенные модели имеют хорошие характеристики (оптимальное значение дисперсии ошибки, точность прогноза, таблица 2).
Произведена оценка АР-моделей с помощью доверительных интервалов рис.5, 6, рассчитаны остатки моделей рис.7, 8.
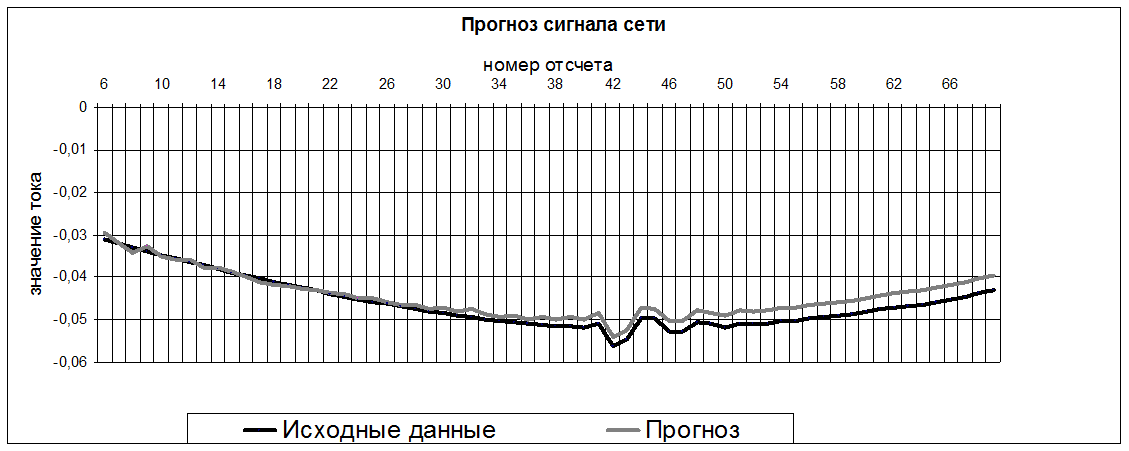
Рис.3. Прогноз сигнала сети с импульсной помехой
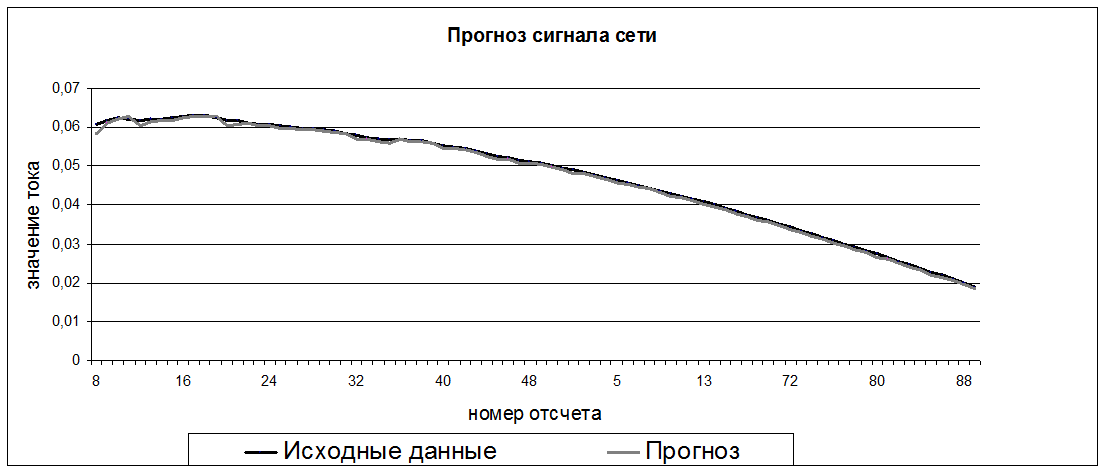
Рис.4. Прогноз сигнала сети с импульсной помехой
Таблица 2. Характеристики АР моделей
|
Вид возмущения |
Вид модели |
Длина временного ряда |
Время упреждения |
Доверительный интервал 95% |
Дисперсия ошибки |
|
Импульсная помеха |
7.4. |
106 |
5 |
0,00644 |
0,0012
|
|
Чистый сигнал |
7.5. |
106 |
5 |
0,021648
|
0,0006
|
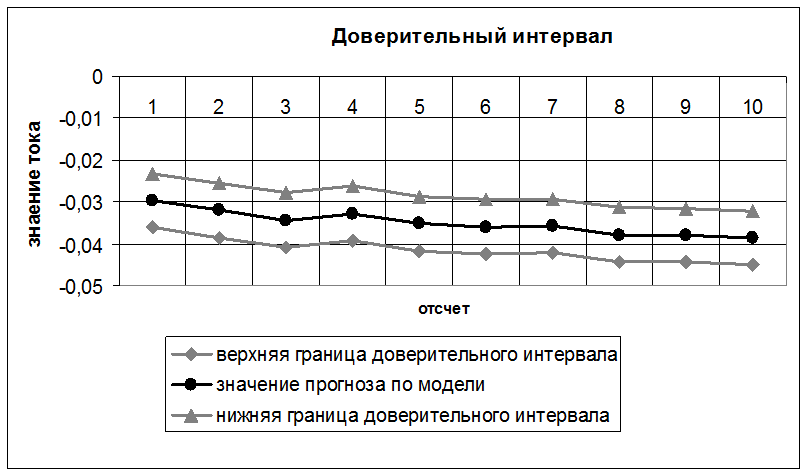
Рис.5. Оценка АР-модели сигнала сети с импульсной помехой с помощью доверительного интервала
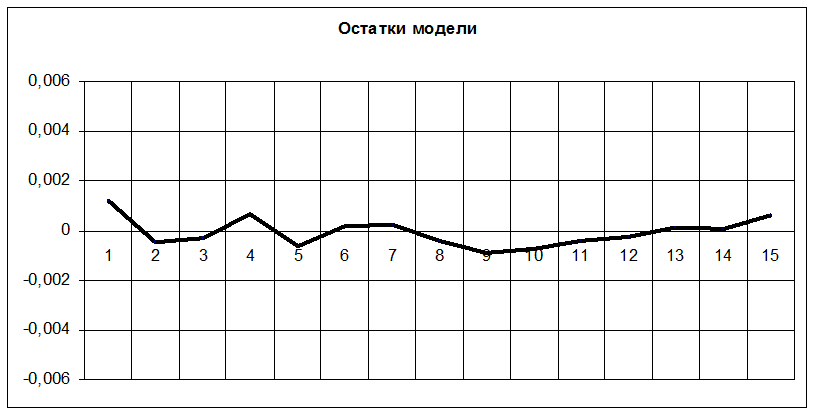
Рис.6. Остатки модели прогноза сигнала сети с импульсной помехой
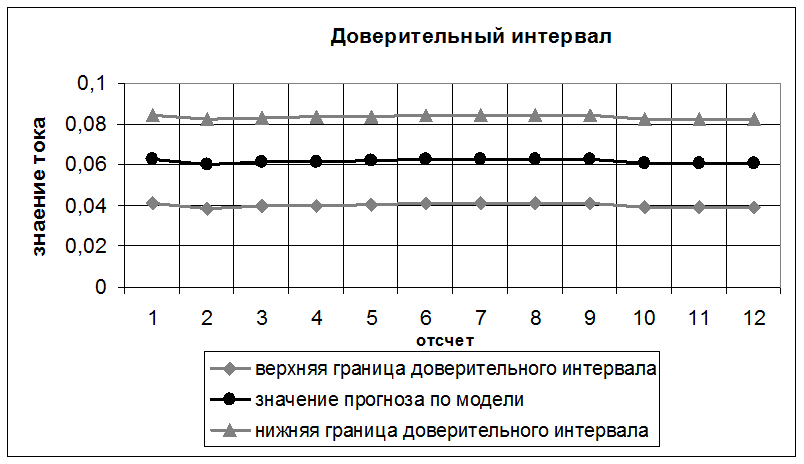
Рис.7. Оценка АР-модели восстановленного по лучшему дереву сигнала с помощью доверительного интервала
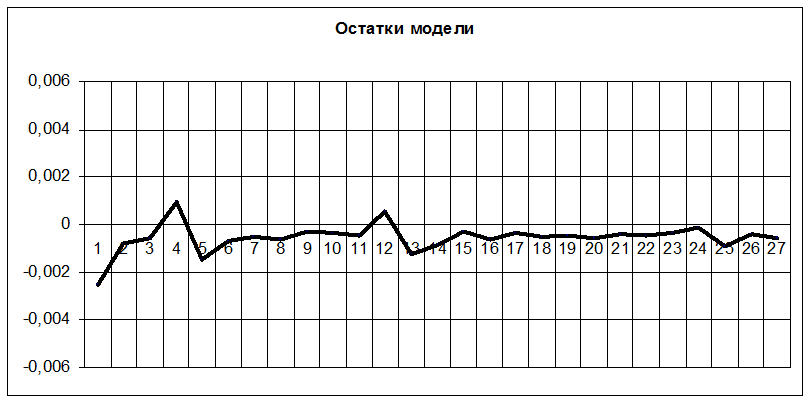
Рис.8. Остатки модели прогноза сигнала, восстановленного по лучшему дереву
Предложена вейвлет технология прогноза сигналов сети без помех и с импульсными помехами.
Проведенные компьютерные эксперименты с моделью подтвердили эффективность построения процедуры прогноза на основе вейвлет технологии, полученные погрешности прогноза сигнала с помехой на уровне 0,1 % от уровня сигнала отличаются примерно в два раза от прогноза сигнала без импульсных помех, что позволит обеспечить 1000 кратное подавление импульсной помехи методами активной фильтрации, что особенно важно для повышения качества напряжения судовой сети электропитания в условиях использования на промысловом судне мощного технологического оборудования с силовыми электронными блоками.
Сведения о рецензентах:
- Шулюпин А.Н., д.т.н., профессор, главный научный сотрудник Научно-исследовательского геотехнологического центра ДВО РАН (НИГТЦ ДВО РАН), г. Петропавловск-Камчатский.
- Пюкке Г.А., д.т.н., профессор, кафедра систем управления, Камчатский государственный технический университет, г. Петропавловск-Камчатский.
Библиографическая ссылка
Горева Т.С., Кузнецов С.Е., Портнягин Н.Н. ПОСТРОЕНИЕ МОДЕЛИ СИГНАЛОВ ЭЛЕКТРИЧЕСКОЙ СЕТИ НА ОСНОВЕ ВЕЙВЛЕТ – КОНСТРУКЦИИ И МОДЕЛИ АВТОРЕГРЕССИИ ПРОИНТЕГРИРОВАННОГО СКОЛЬЗЯЩЕГО СРЕДНЕГО // Современные проблемы науки и образования. – 2011. – № 6. ;URL: https://science-education.ru/ru/article/view?id=5313 (дата обращения: 28.04.2024).



