Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Отений Я.Н. 1 Мартыненко О.В. 1 Эпов А.А. 1

---

1 Камышинский технологический институт (филиал) Государственного образовательного учреждения «Волгоградский государственный технический университет», г. Камышин

В работе были проанализированы особенности течения металла при передвижении ролика по обрабатываемой поверхности при поверхностном пластическом деформировании. Было установлено, что упруго-пластическое течение металла в зоне деформации является основной причиной качественного преобразования поверхностного слоя при поверхностном пластическом деформировании. При этом важно установить особенности течения металла при качении ролика по деформируемой поверхности, используя связи, наложенные на материальные точки, которые расположены на заданной поверхности. Были исследованы составляющие действительных перемещений точек поверхности детали, вычислены траектории, по которым движутся точки поверхности ролика. Рассмотрены варианты перемещения точек деформируемой поверхности по различным кривым и получены математические зависимости, описывающие эти перемещения. Полученные зависимости определяют кинематику точек деформируемой поверхности и могут служить приближенным описанием процесса деформирования.

Статья в формате PDF

245 KB

поверхностный слой.

траектория

ролики

деформирование

1. Дрозд М.С., Федоров А.В., Сидякин Ю.М. Расчет глубины распространения пластической деформации в зоне контакта тел произвольной кривизны // Вестник машиностроения. – 1973. – № 1. – С. 54-57.

2. Мастеров В.А., Беркович В.С. Теория пластической деформации и обработка металлов давлением. – М.: Металлургия, 1989. – 236 с.

3. Папшев Д.Д. Отделочно-упрочняющая обработка ППД. – М.: Машиностроение, 1978. – 150 с.

4. Шнейдер Ю.Г. Технология финишной обработки давлением. – СПб.: Политехник, 1998. – 414 с.

5. Джонсон У., Меллор П. Теория пластичности для инженеров. – М.: Машиностроение, 1979. – 565 с.

Установление  особенностей течения металла  при качении ролика  по деформируемой  упруго-пластической поверхности может быть основано на понятии о связях, наложенных на материальные точки, которые  расположены на заданной поверхности. При условии наложения связей действительное перемещение точек поверхности детали в выбранной системе координат равно геометрической сумме  их совместного перемещения с соприкасаемыми точками ролика  и дополнительного смещения этих же точек относительно поверхности ролика. Вся проблема заключается в установлении этой второй составляющей.

В процессе качения дуги окружности, образуемой при сечении ролика и детали плоскостью, перпендикулярной оси ролика, при отсутствии проскальзывания, нижняя точка О той же окружности (рис.1) является мгновенным центром вращения, то есть неподвижной относительно деформируемой поверхности.

Скорость любой другой точки М (х,z) дуги окружности ролика, находящейся в контакте с деформируемой поверхностью равна:

V_M=ω_P×ρ_м                                    (1)

где: ρ_м - радиус-вектор, проведенный из точки О в точку М (х,у).

Касательная V_км и нормальная V_nм - составляющие этого вектора к дуге указанной окружности - определяются из равенств:

V_n =V_м × cos θ;    V_k =V_м × sin θ                            (2)

где: θ - угол между радиусом-вектором×ρ_м, проведенным из центра окружности О_р в точку М(х,у), и направлением скорости V_м, перпендикулярным радиус-вектору ρ_м.

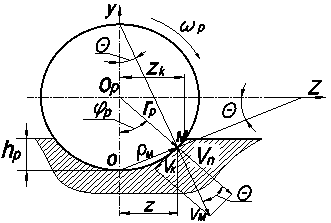
Рис.1. Схема для определения кинематики точек деформируемой поверхности вала без проскальзывания

Для функций sin θ и cos θ имеем следующие соотношения:

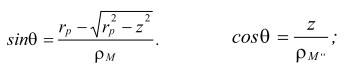                                                 (3)

С учетом этих соотношений получим:

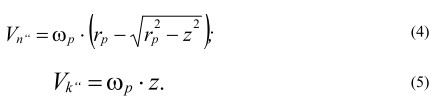
Для вычисления траекторий, по которым движутся точки поверхности ролика, сделаем подстановки:

                     ,

где φ_р - угол контакта, проведенный из центра ролика в точку М([x,y).

Таким образом:

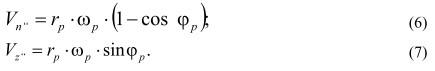
Поскольку:

где t - время перекатывания ролика по поверхности детали, то, интегрируя (6) и (7) по времени, получим:

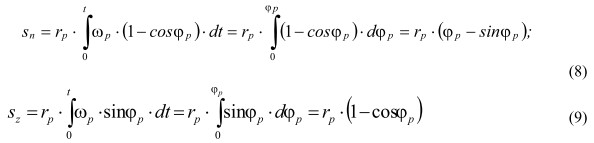
Последние два значения интегралов являются уравнениями циклоид, заданных в параметрической форме.

Поле перемещений точек деформируемой поверхности, описываемое циклоидами (8) и (9), является граничным в том смысле, что действительные траектории не могут быть расположены левее, чем эти траектории. В противном случае, составляющие перемещения будут направлены против сил, выталкивающих металл из зоны обработки, а это невозможно, так как течение металла должно быть направлено в сторону роста напряжений.

Рассмотрим перемещение точек деформируемой поверхности перпендикулярно дугам окружностей, образуемых в сечении ролика при его качении (рис.2, а).  В этом случае дуги окружностей  представляют семейство, описываемое уравнением:

                                              (10)

где: s - параметр семейства окружностей.

В предположении, что точки обрабатываемой поверхности перемещаются перпендикулярно поверхности ролика, заключаем, что их траектории движения совпадают с ортогональными линиями семейства (10).

Для определения уравнения семейства ортогональных кривых продифференцируем уравнение (10) по z:

                                (11)

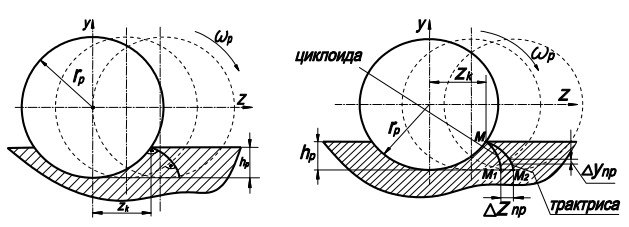
а)                                            б)

Рис.2.  Схема для определения траекторий движения точек деформируемой поверхности перпендикулярно поверхности ролика. Сравнение движения точек деформируемой поверхности по циклоидам и трактрисам

Исключив из двух уравнений (10) и (11) параметр s, получим уравнение:

                     (12)

которое определяет семейство линий, касательных к семейству (10). Заменив в уравнении (12) y′ на 1/y′, получим:

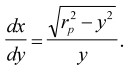
Интеграл этого уравнения определяет семейство траекторий точек деформируемой поверхности в плоскости сечения следующего вида:

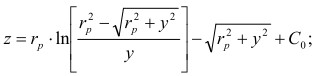                                  (13)

где: С₀ - постоянная характеризующая конкретную точку поверхности детали. Это уравнение трактрисы. В параметрической форме это же уравнение будет иметь вид:

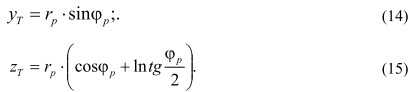
Совместим начала циклоид и трактрис в одной точке М, расположенной  на поверхности ролика (рис.2,б).

Из рисунка видно, что движение по трактрисе можно осуществить в виде суммы двух перемещений: перемещение по участку циклоиды от точки М до М_2, а затем по дуге окружности - от М₁ до М₂. В горизонтальном направлении величина сдвига равна:

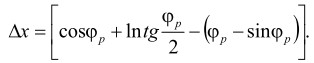                              (16)

Наличием сдвига поверхностного слоя можно объяснить возникновение при ППД преимущественно остаточных напряжений сжатия, т.к. в процессе обработки наружный слой растягивается, причем, чем меньше диаметр ролика при одной и той же глубине внедрения, тем больше растяжение поверхностного слоя.

Аналогичная картина будет наблюдаться для любых других кривых, расположенных правее циклоид.

Библиографическая ссылка