Второй тип конвекции возникает благодаря нагреву по горизонтали. В лабораторном эксперименте, в котором одна стенка вращающегося кольцевого канала нагревается, в то время как другая стена охлаждается, развивается двумерная ячейка в радиально-вертикальной плоскости [6, 7]. Прототипом такого течения является циркуляция Хэдли [3], наблюдаемая в северном и южном полушариях в поясе от экватора до 20°-30° широты. Таким образом, можно назвать движения, поддерживаемые неоднородным нагревом по горизонтали, конвекцией Хэдли. Две разновидности конвекции могут рассматриваться как частные случаи конвекции Рэлея - Хэдли (например, бризовая циркуляция), т.е. движения в средах, в которых существенны градиенты температуры, как по горизонтали, так и по вертикали. В любой физической системе ни решения Рэлея, ни решения Хэдли в чистом виде не могут наблюдаться, потому что, по крайней мере, малые температурные градиенты всегда присутствуют в обоих направлениях.
В настоящей статье проводится численное исследование нелинейной модели двумерной неглубокой конвекции в форме Обербека - Буссинеска, которая реагирует на нагрев, как по горизонтали, так и по вертикали.
Целью работы является исследование влияния горизонтального градиента температуры на устойчивость и форму конвективных ячеек в жидкости.
Рассмотрим безразмерную ограниченную область 
с аспектным отношением A=1. Для численного решения предпочтительно ввести переменную 
(Ω имеет смысл проекции вихря скорости на направление, перпендикулярное плоскости движения) и добавить возмущение температуры в безразмерном виде θ. Тогда система в безразмерных переменных «вихрь Ω- функция тока ψ- температура T- возмущение температуры θ» запишется в виде:
, (1)
, (2)
, (3)
, (4)
где 
- некоторое значение безразмерной температуры на верхней горизонтальной границе при числе Ha=0. Здесь Ra - число Рэлея, Ha - число Хэдли, Pr - число Прандтля. Безразмерные параметры Ra и Ha характеризуют тепловое воздействие по вертикали и горизонтали соответственно.
На границах квадратной области заданы жесткие граничные условия: обращаются в нуль вертикальная и горизонтальная компоненты скорости, возмущения температуры. На горизонтальных и вертикальных границах заданы линейные профили температуры. Положим 
. Задав некоторое начальное распределение вихря скорости и температуры, при помощи уравнений (1) - (4) и краевых условий можно проследить за эволюцией этого начального распределения и, в частности, получить предельный стационарный режим.
Численный метод. Для численного решения задачи применим метод конечных разностей. Введем пространственно-временную сетку:
, 
,
, 
, 
и обозначим 
. Заменяя производные по времени односторонними разностями, а производные по координатам - центральными, получим:
,
, (5)
,(6)
,(7)
. (8)
Значение вихря на стенке получается из условия Вудса второго порядка точности. Уравнение Пуассона (6) решалось итерационным методом Либмана.
Шаг по времени τ выбирался таким образом, чтобы при дальнейшем его уменьшении поля величин оставались неизменными. Основные расчеты проводились на сетке 20x20. Вычисления на более грубой сетке 16x16 и мелкой - 40x40 показали достаточную точность полученного численного решения. При Ha=0 полученные поля функции тока и температуры совпали с имеющимися расчетными данными в [1] при Ra=3500, Ra=8000, Ra=60000. Расчетные графики выполнены на сетке 40x40.
Для поиска стационарных режимов задавалось начальное распределение вихря скорости, и затем отслеживалась его эволюция на безразмерном временном отрезке [0;1]. Такого промежутка было достаточно для установки предельного течения. Число Прандтля во всех расчетах принималось равным 4.0 (для воды Pr=4.8). Начальное распределение температуры было выбрано в виде 
.
Обсуждение результатов. В ходе численных расчетов была показана однозначная зависимость направления циркуляции от знака числа Ha. Задаваемое начальное распределение вихря скорости в виде локального вихря или его отсутствия 
оказалось несущественным для достижения предельного стационарного режима. Развиваясь, начальное возмущение с циркуляцией, обратной предельному стационарному режиму, меняло первоначальное направление вращения на противоположное, и после переходного процесса, продолжительность которого примерно составляла 0.2 безразмерного времени, устанавливалось предельное состояние.
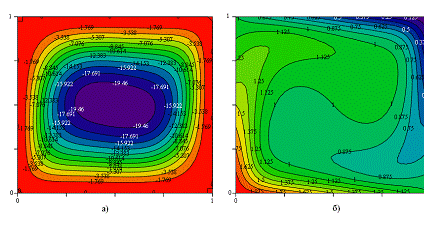
Рисунок 1. Предельный стационарный режим при Ra=60000, Ha<0. Представлены изолинии а) функции тока, б) полной температуры.
С ростом числа Рэлея увеличивалась область изотермического ядра с температурой T=1, что объясняется конвективным перемешиванием. Об интенсивности течения можно судить по максимальным значениям функции тока (Рис 1а). Проводились исследования и в условиях колебательного режима конвекции при больших числах Рэлея. Так, при Ra=600000 была обнаружена система из двух интенсивно вращающихся вихрей относительно общего центра. Теплые потоки жидкости, вытесненные холодным потоком, поднимались наверх и перемещались в область пониженной температуры, где затем диссипировали.
Основной интегральной характеристикой конвективного теплообмена является среднее число Нуссельта, служащее мерой интенсивности конвективного движения. Для задачи (1) - (4) число Нуссельта в момент tn рассчитывалось по формуле:
.
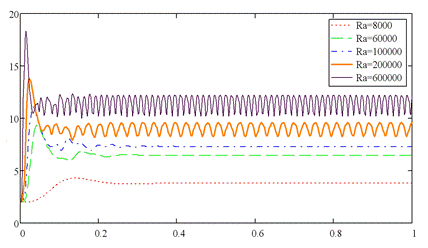
Рисунок 2. Влияние числа Рэлея на установление среднего числа Нуссельта во времени.
Для задачи (1) - (4) зависимость числа Нуссельта от числа Рэлея с графической точностью представляется формулой:
при 
.
На Рис. 2 сравниваются результаты расчетов по установлению во времени среднего числа Нуссельта для различных чисел Ra. Интенсивность конвективного переноса тепла увеличивается с ростом числа Ra. При достижении Ra≈ 2*105 наблюдается колебательный режим; при дальнейшем увеличении растет частота колебаний.
Вывод. Как указано в [4], данные расчетов с жесткими граничными условиями лучше соответствует экспериментальным данным. Добавление горизонтальной неоднородности температуры вместе с жесткими граничными условиями усилило устойчивость конвективных течений, что является важным фактором их реализуемости в реальной жидкости (или атмосфере).
Таким образом, в работе численно исследована общая конвективная модель, более точно воспроизводящая наблюдаемые режимы конвекции. Показано, что неизбежно возникающие в реальной атмосфере горизонтальные градиенты существенно влияют на характер течений.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг. (№ 02.740.11.0739).
Рецензенты:
- Диканский Ю.И., д.ф.-м.н., профессор, заведующий кафедрой общей физики ФГБОУ ВПО «Ставропольский государственный университет», г. Ставрополь.
- Симоновский А.Я., д.ф.-м.н., профессор, профессор кафедры теоретической физики ФГБОУ ВПО «Ставропольский государственный университет», г. Ставрополь.
Библиографическая ссылка
Закинян Р.Г., Сухов С.А., Ларченко И.Н. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВОЙ КОНВЕКЦИИ // Современные проблемы науки и образования. – 2011. – № 6. ;URL: https://science-education.ru/ru/article/view?id=5016 (дата обращения: 16.04.2024).