Целью данной работы, является разработка математической модели расчета эффективного упругого модуля характерного объема материала путем осреднения по всем реализациям случайного поля неоднородностей с учетом их концентрации и пространственной ориентации.
Рассмотрим композиционный материал на примере полиминеральной равномерно-зернистой структуры - зёрна изометрические, округлой формы одного минерала окружены зернами другого. Например, амфибол вокруг зерен пироксена в некоторых перидотитах. Допускаются зерна угловатой, цилиндрической, призматической и игольчатой форм одного минерала, окруженные зернами другого.
Пусть объем V ≥ VC заполнен горной породой, где VC - объем, образованный почти одинаковыми размерами зерен цилиндрической, призматической или игольчатой формы, плотно примыкающих друг к другу. Зерна округлой формы, включения имеют форму эллипсоида, зерна призматической и цилиндрической формы - вытянутого эллипсоида, зерна игольчатой формы - тонкого вытянутого эллипсоида. Включениями будут зерна одного минерала по отношению к основному минералу в количественном отношении, который назовем основной средой или матрицей. При моделировании таких систем отвлечемся от поликристаллического строения матрицы путем ее замены на эквивалентную упругую среду с эффективными константами, которые находим, применяя модель «K» [3].
В результате мы заменим в первом приближении рассматриваемые горные породы эквивалентной им однородной упругой средой с эллипсоидальными неоднородностями. Поскольку расположение зерен минералов носит случайный характер, то мы имеем модель композитной среды, содержащей случайное изотропное поле эллипсоидальных неоднородностей. Теперь определим эффективные свойства этой среды.
Итак, рассмотрим неограниченную трехмерную упругую однородную среду (основную) с неоднородностями в эллипсоидальных областях Vi. Назовем ее моделью «L». Свойство основной среды определяет тензор эффективных модулей упругости Е э
(1)
где I - единичный тензор, E - постоянный тензор модуля упругости структурной составляющей, E1 = E - <E> - случайный тензор, постоянный в пределах каждой неоднородности, 
- постоянный тензор, представляющий собой среднее значение от Фурье образа второй производной тензора Грина на единичной сфере,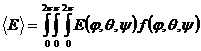 
- среднее значение модуля упругости, 
- функция распределения структурных составляющих по ориентациям, i, j, k, l, m, n, r, t, p, q = 1, 2, 3.
Обозначим через 
непрерывное внешнее поле деформаций, которое при заданных внешних силах (включая условия на бесконечности) существовало бы при Е1 = 0 в однородной среде, и через 
- кусочно-непрерывное поле деформаций в среде с неоднородностями при тех же внешних условиях. Согласно [3], для тензора 
имеем уравнение:
(2)
где 
- оператор, имеющий ядро 
, Θ (r) - характеристическая функция области V, занятой неоднородностями. Если 
- точка среды с радиус-вектором r, то Θ(r) = 1 при 
и Θ (r) = 0 при 
.
Следовательно, поле деформаций ε внутри неоднородности удовлетворяет уравнению:
(3)
Воспользуемся методом эквивалентного поля, предположения которого изложены в работе проф. К.В. Халкечева [4]. В рамках этого метода поле деформаций ε внутри любой неоднородности определяется следующим образом:
(4)
Подставляя из последнего уравнения значение ε(r) в (3) и усредняя результат по ансамблю полей неоднородности, получим уравнение относительно ε´:
(5)
где 
- концентрация неоднородностей.
Концентрация п требует дополнительного определения в данном случае, поскольку среди характеристик горной породы имеется конечный объем V ≥ VC, а соответствующая модель предполагает среду неограниченной. Наличие такой характеристики, как конечный объем, указывает, что в число характеристик должны включаться характеристики поверхности, ограничивающей рассматриваемый объем. Чтобы избавиться от поверхности и тем самым прийти к модели неограниченной среды, можно прибегнуть к чисто математическому приему предельного перехода по Боголюбову. Если V - объем горной породы, а N - число неоднородностей, то совершают предельный переход N→∞ ,V→∞ (переход к бесконечной среде), но так, что величина N/V=1/υ остается такой же, как и в реальной горной породе, т.е. υ - конечная величина. Тогда все объемные свойства бесконечной среды совпадают со свойствами реальной горной породы, а в качестве характеристики вместо объема горной породы можно рассматривать величину υ - средний объем, приходящийся на одну неоднородность. Поэтому вместо концентрации п можно использовать аналог 1/υ - среднюю плотность числа неоднородностей.
В среднее 
под интегралом (5) вклад дают лишь те реализации, для которых 
принимает ненулевые значения. Поскольку 
- характеристическая функция области VH, занятой неоднородностями, то 
, если точки r и r´ одновременно попадают внутрь области VН. Причем эти точки могут одновременно попадать внутрь одной неоднородности или же в разные. В связи с этим рассматриваемое среднее для случая равномерно распределенных неоднородностей (допускается построение ячеек типа Вигнера - Зейтца) можно представить в виде суммы:
, (6)
где 
- часть, связанная с попаданием точек r и r´ внутрь одной и той же неоднородности; 
- часть, связанная с попаданием точек в разные неоднородности.
(7)
где 
- объем внутри эллипсоидальной области, занятой неоднородностью с полуосями 
, попадание в которую точки r´ гарантирует попадание точки r в тот же эллипсоид; Q - ортогональный случайный тензор, определяющий ориентацию неоднородности в пространстве. Осреднение (7) проводится по ансамблю функций распределения размеров неоднородностей и их свойств [2]. Функцию 
сведем к сферически-симметричной путем аффинного преобразования, переводящего эллипсоид в единичный шар:
.
Подставим (6) в (5):
(8)
Для однородных эргодичных полей неоднородностей
(9)
где 
- объем эллипсоида; усреднение в левой части производится по ансамблю реализаций случайного поля, а в правой среднее ищется от случайной величины, функция распределения которой определяется ансамблевыми функциями распределения размеров включений и их свойств. А интеграл в (8) после ряда выкладок имеет вид:
(10)
Подставим (9) и (10) в (8), после несложных преобразований для эквивалентного поля деформаций имеем уравнение:
. (11)
Поле деформаций внутри любой неоднородности определится в рамках метода эквивалентного поля из (4) и (11) следующим образом:
, (12)
Отсюда средняя деформация <ε> среды с неоднородностями можем получить, подставляя (12) в (2), а результат усредним по ансамблю реализаций:
×
, (13)
где 
.
В этом выражении интеграл расходится в нуле и на бесконечности. Среднее, входящее под знак интеграла, образует постоянный двухвалентный тензор. Таким образом, необходима регуляризация данного интеграла. Этот интеграл не допускает однозначной естественной регуляризации, его значение определяется тем смыслом, который он имеет в рассматриваемой задаче.
Пусть поле напряжений в среде постоянно и равно внешнему полю 
, а также предположим, что Е1 в (2) - постоянный тензор. Это соответствует среде, в которой неоднородность «размазана» по всей среде. Очевидно, что тензор упругих модулей такой среды равен 
. Отсюда тензор деформаций этой среды:
(14)
Теперь необходимо решение уравнения (2) свести к виду (14). Такое возможно, если регуляризацию интеграла определить соотношением:
, 
(15)
Действительно, имеем из (2) 
.
Подействуем на обе части уравнений слева оператором Еэ:
.
Отсюда 
,что совпадает с (14).
Используем регуляризацию (15) в соответствии с указанным ей смыслом для интеграла в (13). В результате имеем:
, (16)
Из (15) и (16):
, (17)
Для построения функции Ф2(R) под интегралом в данном выражении необходимо задаться конкретной моделью случайного поля неоднородностей в среде.
Таким образом, для того чтобы определить эффективные упругие характеристики биминеральных горных пород равномерно-зернистой структуры, необходимо применить последовательно две модели «K» и «L», что обозначим через «K» + «L».
Аналогично можно определить эффективные упругие характеристики полиминеральных горных пород равномерно-зернистой структуры из трех минеральных составляющих, необходимо применить последовательно модели («K» + «L») + «L».
(18)
где 
; А построена для среды с эффективными свойствами 
.
На основе разработанной модели была проведена численная реализация по расчету эффективного модуля податливости мерзлого каменного угля, что удовлетворительно согласуется с экспериментальными данными [5]. Получены следующие результаты в единицах 10-10 Па: 
или в матричной форме,
.
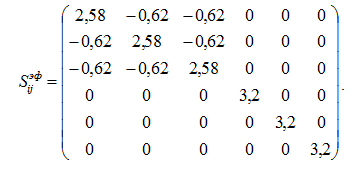На основании полученных результатов можно заключить, что построенная математическая модель позволяет с минимальной погрешностью определить эффективные свойства многокомпонентных материалов.
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы, по ГК № П 1105, ГК № П 1122 от 02.06.2010 г.
Рецензенты:
- Борлаков Х.Ш., д.ф.-м.н., профессор, профессор кафедры физики, ФГБОУ ВПО «Северо-Кавказская государственная гуманитарно-технологическая академия» Министерство образования и науки РФ, г. Черкесск.
- Боташев А.Ю., д.т.н., профессор, директор инженерно-технологического института, ФГБОУ ВПО «Северо-Кавказская государственная гуманитарно-технологическая академия» Министерство образования и науки РФ, г. Черкесск.
Работа получена 07.11.2011
Библиографическая ссылка
Шайлиев Р.Ш. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСЧЕТА ЭФФЕКТИВНЫХ СВОЙСТВ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ НА ПРИМЕРЕ ПОЛИМИНЕРАЛЬНЫХ ГОРНЫХ ПОРОД // Современные проблемы науки и образования. – 2011. – № 5. ;URL: https://science-education.ru/ru/article/view?id=4925 (дата обращения: 10.11.2024).