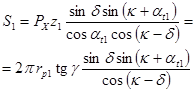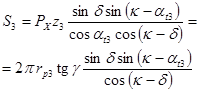Планетарные роликовинтовые механизмы (РВМ) преобразуют вращательное движение в поступательное и используются в приводах станков, авиационных систем, подъемно-транспортного оборудования, медицины в качестве эффективных исполнительных устройств. Одной из важнейших задач для РВМ с фрикционным характером зацепления является определение кинематических характеристик, которые обеспечивают требуемые перемещения [1]. В данной статье предложен подход к определению кинематических характеристик РВМ с фрикционным характером зацепления (рис.1).
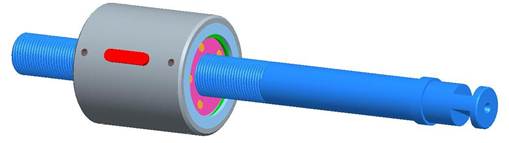
а) в собранном виде
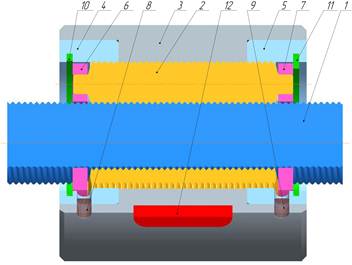
б) разрез: 1 - винт, 2 - ролики, 3 - гайка, 4 ‑ венец зубчатый, 5 - венец зубчатый, 6- сепаратор, 7 - сепаратор,8 ‑ штифт, 9 - штифт, 10 - стопорное кольцо, 11 - стопорное кольцо, 12 ‑ шпонка
Рис. 1. РВМ с фрикционным характером зацепления (Компас 3D v9)
В общем случае РВМ состоит из резьбовых элементов: винта, роликов-сателлитов, гайки и нерезьбовых элементов: сепараторов, зубчатых венцов, стопорных колец. Для обеспечения синхронизации вращения на резьбовых роликах дополнительно нарезаны зубчатые канавки.
РВМ принято различать по следующим признакам [1]: какое из зацеплений роликов - с гайкой или винтом - является опорным, а какое - рабочим; какое из звеньев РВМ - винт или гайка - является входным (ведущим), а какое - выходным (ведомым); каково соотношение углов подъема и направлений нарезок винта, роликов и гайки, что определяет тип зацепления звеньев в торцовом сечении: дополюсное, заполюсное или внутреннее. Эти типы зацеплений определяются соотношением углов подъема и направлений нарезок винта, роликов и гайки. Угол подъема определяется по известной формуле ![]() , где PX - осевой шаг винтовой линии (мм); zi - число заходов на i-м звене; ri - средний (рабочий) радиус i-го звена. Индекс i = 1 обозначает, что параметр относится к винту; i = 2 - к ролику; i = 3 - к гайке. Возможные сочетания углов подъема, приводящие к различным группам РВМ, приведены в табл. 1.
, где PX - осевой шаг винтовой линии (мм); zi - число заходов на i-м звене; ri - средний (рабочий) радиус i-го звена. Индекс i = 1 обозначает, что параметр относится к винту; i = 2 - к ролику; i = 3 - к гайке. Возможные сочетания углов подъема, приводящие к различным группам РВМ, приведены в табл. 1.
Таблица 1. Варианты исполнения роликовинтовых механизмов
|
Группа |
Соотношение углов подъема |
Направление |
Соотношение углов подъема |
Направление |
|
Опорная гайка ( |
Опорный винт ( |
|||
|
1 |
|
противоположное |
|
одинаковое |
|
2 |
|
противоположное |
|
одинаковое |
|
3 |
любое |
одинаковое |
любое |
противоположное |
В большинстве вариантов (за исключением частных случаев подшипника и передачи типа Transroll) РВМ не является передачей зацеплением, поэтому возникает вопрос о существовании фрикционной связи в рабочем сопряжении, достаточной для передачи движения.
Достаточность сцепления определяется величиной угла δ отклонения проекции силы трения от перпендикуляра к нормали: чем ближе угол δ к 90°, тем сильнее связь между звеньями в тяговом режиме прямого хода.
Угол трения δ находится из квадратного уравнения [2]:
![]() , (1)
, (1)
где ![]() ; γ - угол наклона нормали в точке контакта; κ - угол отклонения точки контакта от линии центров;
; γ - угол наклона нормали в точке контакта; κ - угол отклонения точки контакта от линии центров; ![]() - половина угла профиля резьбы; f - коэффициент трения скольжения.
- половина угла профиля резьбы; f - коэффициент трения скольжения.
Умножая обе части уравнения (1) на ![]() , получаем
, получаем
![]() .
.
Последнее уравнение приводится к квадратному уравнению
![]() ,
,
решение которого имеет два корня
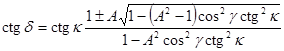 .
.
Соответствующий корень следует выбирать из условия: «+» - при ![]() , «-» - при
, «-» - при ![]() . Обе ветви можно записать общей формулой
. Обе ветви можно записать общей формулой
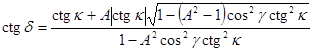 . (2)
. (2)
Дискриминант уравнения (1) обращается в ноль при ![]() . Тогда
. Тогда ![]() , что соответствует передаче зацеплением.
, что соответствует передаче зацеплением.
Корни (2) существуют при выполнении условия достаточности сцепления (положительности знаменателя):
![]() . (3)
. (3)
Условие (3) эквивалентно неравенству 0 < δ < π, которое определяет область существования фрикционных РВМ. Максимальное значение показателя сцепления ![]() достигается для передачи зацеплением. Для остальных типов РВМ показатель строго меньше 1 на квадрат величины
достигается для передачи зацеплением. Для остальных типов РВМ показатель строго меньше 1 на квадрат величины
![]() , (4)
, (4)
которая является важной характеристикой фрикционной передачи и для краткости будет называться фрикционным параметром. Его использование для оценки «фрикционности» передачи более удобно, чем определенного в [1] фрикционного параметра A, т.к. он имеет свойства показателя: ![]() - для работоспособных передач,
- для работоспособных передач, ![]() - для передачи зацеплением и
- для передачи зацеплением и ![]() - для передач, лежащих за пределами области сцепления.
- для передач, лежащих за пределами области сцепления.
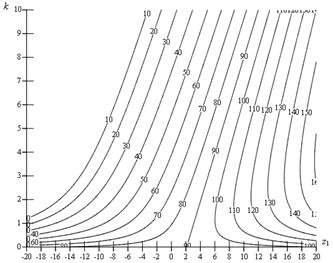
На рис. 2, а показаны линии уровня угла δ как функции двух переменных ![]() при значении
при значении ![]() и коэффициента трения
и коэффициента трения ![]() .
.
а)
б)
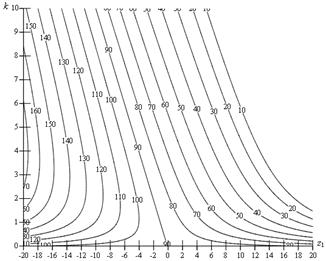
Рис. 2. Линии уровня угла трения δ при z2 = +1: а - опорная гайка; б - опорный винт
Линии уровня δ = const представляют собой гиперболические кривые с асимптотами
k=0 и 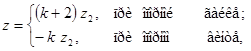 (5)
(5)
вдоль которых ![]() .
.
На размеры и расположение области сцепления 0 < δ < π существенно влияет значение коэффициента трения, при его уменьшении область теснее прижимается к асимптотам. Другим предельным случаем поведения угла трения является асимптотика при ![]() :
:
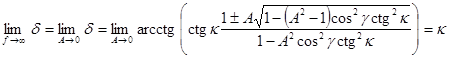 . (6)
. (6)
т.е. угол трения при наличии идеальной фрикционной связи равен углу отклонения точки контакта от линии центров.
На рис. 2, б показаны линии уровня угла κ в зависимости от отношения k и числа заходов на рабочем звене z. Таким образом, анализ угла трения как основного фактора фрикционного сцепления в рабочем сопряжении РВМ показал наличие существенной связи между трением и кинематической способностью РВМ. Однако для получения количественной зависимости необходимо исследовать влияние трения на кинематическую передаточную функцию РВМ.
Наиболее информативным кинематическим параметром РВМ является кинематическая передаточная функция (КПФ), методики расчета которой были опубликованы [1], поэтому в табл. 2 приводится последовательность расчета КПФ РВМ без подробных пояснений. Формулы даны так, чтобы КПФ имела размерность [мм/об]. Приведены два варианта формул КПФ, через ![]() и средний радиус, т.к. первый вариант имеет особенность 0/0 при z=0 и следует пользоваться вторым вариантом. Из табл. 2 следует, что для однозначного определения КПФ в общем случае требуется задание условия, какое звено является рабочим, и 7 независимых параметров: числа заходов на рабочем звене z1 (или z3), числа заходов на ролике z2, отношения диаметра винта к диаметру ролика k, диаметра винта r1, осевого шага PX, угла профиля резьбы αX, коэффициента трения f, причем первые три параметра должны быть целочисленными.
и средний радиус, т.к. первый вариант имеет особенность 0/0 при z=0 и следует пользоваться вторым вариантом. Из табл. 2 следует, что для однозначного определения КПФ в общем случае требуется задание условия, какое звено является рабочим, и 7 независимых параметров: числа заходов на рабочем звене z1 (или z3), числа заходов на ролике z2, отношения диаметра винта к диаметру ролика k, диаметра винта r1, осевого шага PX, угла профиля резьбы αX, коэффициента трения f, причем первые три параметра должны быть целочисленными.
Таблица 2. Методика расчета кинематической передаточной функции РВМ
|
Опорная гайка |
Опорный винт |
|
|
|
В таблице обозначено: ![]() - торцовый угол профиля, δ - угол трения;
- торцовый угол профиля, δ - угол трения; ![]() - угол отклонения точки контакта от линии центров;
- угол отклонения точки контакта от линии центров; ![]() - средние (рабочие) радиусы звеньев
- средние (рабочие) радиусы звеньев ![]() - угол наклона нормали в точке контакта
- угол наклона нормали в точке контакта
На рис. 3 показаны линии уровня КПФ как функции двух переменных ![]() по формулам табл.2 при значении коэффициента трения f = 0,15. При численном расчете приняты следующие значения остальных значимых параметров: осевой шаг PX = 1 мм, половина угла профиля резьбы αX = 45°. Следует обратить внимание, что характер линий уровня в случае опорной гайки отличается от линий уровня при опорном винте. Это связано с различием в поведении КПФ при
по формулам табл.2 при значении коэффициента трения f = 0,15. При численном расчете приняты следующие значения остальных значимых параметров: осевой шаг PX = 1 мм, половина угла профиля резьбы αX = 45°. Следует обратить внимание, что характер линий уровня в случае опорной гайки отличается от линий уровня при опорном винте. Это связано с различием в поведении КПФ при ![]() :
:
![]() ;
; ![]() , (7)
, (7)
т.е. при k=0 РВМ в случае опорной гайки вырождается в передачу зацеплением трансролл, а в случае опорного винта - в подшипник.
При наличии идеальной фрикционной связи КПФ определяется как предел при f→∞:
![]() ; (8)
; (8)
![]() . (9)
. (9)
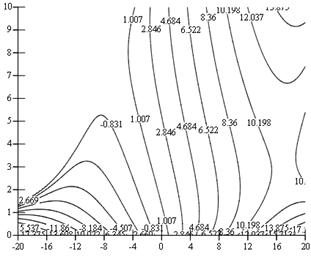
а)
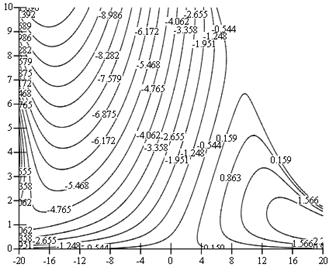
б)
Рис. 2. Линии уровня КПФ при z2 = +1 и f = 0,15: а - опорная гайка; б - опорный винт
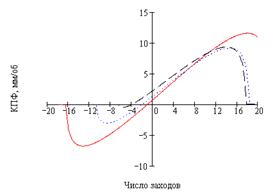
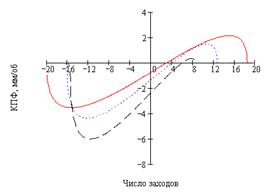
В заключение численного исследования построим семейства графиков КПФ как функции от числа заходов z на рабочем звене при фиксированных значениях отношения k и при f = 0,15 (сечения поверхностей плоскостями k=const): на рис. 3 - для z2=+1.
|
а) |
б) |
|
Рис. 3. Зависимость КПФ от числа заходов при z2 = +1 и f = 0,15: а - опорная гайка; б - опорный винт (--- k = 1; - - - k = 2; - - - k = 4) |
|
В случае опорной гайки (рис. 3, а) участок ![]() графика соответствует передачам 1-й группы;
графика соответствует передачам 1-й группы; ![]() - передачам 2-й группы;
- передачам 2-й группы; ![]() - передачам 3-й группы. Аналогично, в случае опорного винта (рис. 3, б) участок
- передачам 3-й группы. Аналогично, в случае опорного винта (рис. 3, б) участок ![]() соответствует передачам 1-й группы;
соответствует передачам 1-й группы; ![]() - передачам 2-й группы;
- передачам 2-й группы; ![]() - передачам 3-й группы.
- передачам 3-й группы.
Каждый график рис. 3 разбивается на линейный участок, когда КПФ прямо пропорционально зависит от числа заходов, и участки срыва, когда дальнейшее изменение z ведет к резкому падению SX до нуля. Для выяснения причин такого поведения следует провести анализ зависимости SX от геометрических и фрикционных параметров РВМ. Ниже будет показано, что участок линейности соответствует области стабильности РВМ, а участки срыва свидетельствуют о нарушении фрикционной стабильности.
Рецензенты:
- 1. Гоц А.Н., д.т.н., профессор, профессор кафедры тепловых двигателей и энергетических установок ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых».
- 2. Житников Б.Ю., д.т.н., профессор, профессор кафедры специальной техники и информационных технологий ФГОУ ВПО ВЮИ ФСИН России.
Библиографическая ссылка
Морозов В.В. КИНЕМАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛАНЕТАРНЫХ РОЛИКОВИНТОВЫХ МЕХАНИЗМОВ С ФРИКЦИОННЫМ ХАРАКТЕРОМ ЗАЦЕПЛЕНИЯ // Современные проблемы науки и образования. 2011. № 6. ;URL: https://science-education.ru/ru/article/view?id=4918 (дата обращения: 29.06.2025).