В работе рассмотрены особенности формирования поверхностей разрушения для поликристаллов с гексагональной плотноупакованной (ГПУ) кристаллической решёткой для статистического критерия ориентированного разрушения [1,2]. При его получении предполагалось, что микротрещины возникают на площадках ортогональных σ1. Использован локальный критерий прочности ![]() , что является приемлемой гипотезой, когда зёрна обладают малой прочностной анизотропией. Например, когда кристаллы не имеют особых плоскостей спайности (отдельности) или, напротив, имеют большое число таких плоскостей. Условие ориентированного разрушения имеет вид:
, что является приемлемой гипотезой, когда зёрна обладают малой прочностной анизотропией. Например, когда кристаллы не имеют особых плоскостей спайности (отдельности) или, напротив, имеют большое число таких плоскостей. Условие ориентированного разрушения имеет вид:
![]() (1)
(1)
где 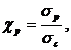 а
а ![]() - истинные разрушающие напряжения при растяжении и сжатии,
- истинные разрушающие напряжения при растяжении и сжатии, 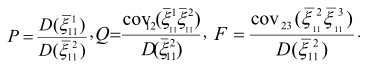
Здесь ![]() дисперсии,
дисперсии,![]() =
= ![]() ковариации микронапряжений
ковариации микронапряжений ![]() , коллинеарных главному макроскопическому напряжению σ1. На
, коллинеарных главному макроскопическому напряжению σ1. На ![]() накладывается ограничение
накладывается ограничение ![]() которое следует из физических предпосылок рассматриваемого критерия, а именно: локальная прочность
которое следует из физических предпосылок рассматриваемого критерия, а именно: локальная прочность ![]() не может быть отрицательной. Для поликристаллов с кубической кристаллической решёткой параметры P, Q, F, определённые на модели поликристалла с использованием гипотезы Фойгта об однородности деформаций, являются константами Р=16/9, Q=-8/9, F=-1/9. Расчёт микронапряжений на модели поликристалла методом конечных элементов для этих материалов [1] дал сравнительно узкий интервал значений P, Q и F, что позволило представить рассматриваемый критерий в более компактной форме [2], включающей в себя только два структурно-чувствительных параметра σp , σc.
не может быть отрицательной. Для поликристаллов с кубической кристаллической решёткой параметры P, Q, F, определённые на модели поликристалла с использованием гипотезы Фойгта об однородности деформаций, являются константами Р=16/9, Q=-8/9, F=-1/9. Расчёт микронапряжений на модели поликристалла методом конечных элементов для этих материалов [1] дал сравнительно узкий интервал значений P, Q и F, что позволило представить рассматриваемый критерий в более компактной форме [2], включающей в себя только два структурно-чувствительных параметра σp , σc.
Однако, как показали проведённые расчёты для поликристаллов с ГПУ решёткой, величины параметров P, Q, F и, следовательно, коэффициенты корреляции для различных материалов резко отличаются. Это связано с тем, что упругие свойства зёрен у них обладают меньшей симметрией свойств по сравнению с кубическими. Микронапряжения ![]() (k=1, 2, 3) определяются на модели поликристалла при использовании гипотезы Фойгта при рассмотрении трёх одноосных растяжений под действием главных единичных макроскопических напряжений σk, а затем вычисляются дисперсии и ковариации [3].
(k=1, 2, 3) определяются на модели поликристалла при использовании гипотезы Фойгта при рассмотрении трёх одноосных растяжений под действием главных единичных макроскопических напряжений σk, а затем вычисляются дисперсии и ковариации [3].
В работе [3] показано существенное отличие закономерностей изменения дисперсий нормальных напряжений, отнесённых к главному макроскопическому ![]() , в зависимости от вида напряжённого состояния для ряда ГПУ - поликристаллов.
, в зависимости от вида напряжённого состояния для ряда ГПУ - поликристаллов.
Покажем, как это сказывается на форме поверхности разрушения на примере критерия (1). В силу квазииизотропности поликристалла ![]() , поэтому параметр
, поэтому параметр ![]() . Легко показать, что
. Легко показать, что ![]() Здесь
Здесь ![]() и
и ![]() коэффициенты корреляции
коэффициенты корреляции ![]() . В таблице 1 приведены результаты расчёта P, Q, F и
. В таблице 1 приведены результаты расчёта P, Q, F и ![]() и
и ![]() для ряда материалов с ГПУ решёткой с использованием гипотезы Фойгта. Кроме того, там для
для ряда материалов с ГПУ решёткой с использованием гипотезы Фойгта. Кроме того, там для ![]() даны результаты расчёта по критерию (1) относительной прочности
даны результаты расчёта по критерию (1) относительной прочности ![]() при трёхосном гидростатическом растяжении и при двухосном растяжении
при трёхосном гидростатическом растяжении и при двухосном растяжении ![]() , а также
, а также ![]() для двухосного сжатия.
для двухосного сжатия.
Таблица 1
Результаты расчёта параметров P, Q, F по Фойгту для ГПУ поликристаллов и
относительная прочность для трёх видов напряжённого состояния при ![]()
|
Материал |
P |
Q |
F=ρ23 |
ρ12 |
3х осн. раст. |
2х осн. раст. |
2х осн. сжат. |
|
Cd |
11,64 |
-3,386 |
0,972 |
-0,9926 |
1,984 |
1,329 |
-2,014 |
|
Zn |
9,484 |
-2,758 |
0,614 |
-0,8956 |
1,805 |
1,27 |
-2,226 |
|
Be |
5,191 |
-1,258 |
-0,346 |
-0,5521 |
1,364 |
1,099 |
-3,497 |
|
Co |
1,065 |
-0,555 |
-0,419 |
-0,5378 |
1,311 |
1,014 |
-3,711 |
|
In |
0,852 |
-0,436 |
-0,551 |
-0,4724 |
1,268 |
0,984 |
-4,221 |
|
Ti |
0,751 |
-0,402 |
-0,569 |
-0,4639 |
1,248 |
0,974 |
-4,308 |
|
Sn |
1,856 |
-0,325 |
-0,764 |
-0,2386 |
1,095 |
0,97 |
-5,822 |
|
Y |
0,576 |
-0,109 |
-0,755 |
-0,1436 |
0,991 |
0,908 |
-5,714 |
Можно видеть, что ![]() для всех рассмотренных материалов, причём, чем меньше ρ12, тем больше прочность при двухосном (рис. 1) и трёхосном растяжении (табл. 1). Заметим, что чем меньше
для всех рассмотренных материалов, причём, чем меньше ρ12, тем больше прочность при двухосном (рис. 1) и трёхосном растяжении (табл. 1). Заметим, что чем меньше ![]() , тем больше
, тем больше ![]() . Величина ρ23 определяет прочность при двухосном сжатии, причём, чем она меньше, тем прочность больше (рисунок).
. Величина ρ23 определяет прочность при двухосном сжатии, причём, чем она меньше, тем прочность больше (рисунок).
Увеличение прочности при уменьшении ρ12 и ρ23 , когда главные макронапряжения имеют одинаковый знак, связано с тем, что взаимодействие зёрен при отрицательных коэффициентах корреляции приводит к уменьшению концентрации растягивающих микронапряжений ξ11 по сравнению с одноосным растяжением.
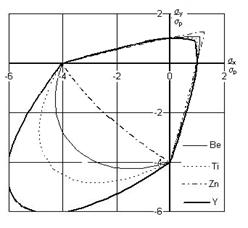
Теоретические контуры разрушения для плоского напряжённого состояния
поликристаллов с ГПУ решёткой при c=0,25, соответствующие критерию (1),
построенные по параметрам табл. 1
Список литературы
- Багмутов B.П., Богданов Е.П. О возможности учёта типа кристаллической решётки и анизотропии прочности зёрен в критериях разрушения. Проблемы машиностроения и надёжности, №1. 2004. - С. 24-30.
- Багмутов B.П., Богданов Е.П. Микронеоднородное деформирование и статистические критерии прочности и пластичности: Монография/ ВолгГТУ. - Волгоград, 2003. - С. 358 .
- Богданов Е.П., Шкода И.А. Микровзаимодействия анизотропных зёрен и вид поверхности разрушения/Сборник трудов Пятой Всероссийской конференции "Математическое моделирование и краевые задачи" (ММ-2007): Самарский государственный технический университет. - г. Самара, 2008. - С. 62-65.
Библиографическая ссылка
Богданов Е.П., Шкода И.А. ПОВЕРХНОСТИ РАЗРУШЕНИЯ ДЛЯ ПОЛИКРИСТАЛЛОВ С ГЕКСАГОНАЛЬНОЙ ПЛОТНОУПАКОВАННОЙ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКОЙ ДЛЯ // Современные проблемы науки и образования. 2010. № 5. ;URL: https://science-education.ru/ru/article/view?id=4523 (дата обращения: 18.11.2025).



