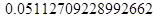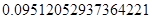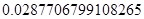Компетенции, получаемые студентами вузов при изучении теории вероятностей и математической статистики, находят широкое применение в научных теоретических и, преимущественно, практико-ориентированных исследованиях, относящихся к различным отраслям человеческой деятельности [1, 2, 3]. В то же время преподавание теории вероятностей на 1–2-м курсах вуза не позволяет обучающимся в полной мере оценить возможности и ограничения вероятностных моделей процессов и явлений. Во многом это объясняется ориентацией значительной части преподавателей на развитие комбинаторных умений студентов и концентрацией их внимания на вычислительных процедурах [4]. Тем не менее авторы выявили несколько вузовских научно-методических групп, которые разрабатывают активные методы преподавания вероятностных дисциплин, такие как решение ситуационных задач [5], метод проектов, математические бои, деловые игры [6], а также проектируют программы дисциплины, ориентируясь на направление подготовки [7].
Именно моделирование является одним из основных компонентов научного и инженерного творчества. Вопросы точности стохастических моделей обычно всегда остаются вне поля зрения педагогов-математиков. Более того, эти вопросы практически не затрагиваются в популярных учебниках и руководствах по теории вероятностей. В настоящем исследовании авторы делают попытку найти достаточно простые методические приемы для ликвидации этого пробела.
Целью настоящего исследования является разработка таких методик преподавания некоторых разделов теории вероятности, которые позволяют наглядно продемонстрировать студентам подходы к оценке точности вероятностных моделей. Авторы предлагают для внедрения в практику преподавания несколько конкретных примеров, снабженных визуализацией, с целью облегчения восприятия молодыми людьми новой для них информации. Приведенные примеры могут быть легко трансформированы с целью соответствия предметной области обучающихся. Также авторы дают рекомендации по локализации разработанных методик для различных образовательных программ.
Материал и методы исследования
Во-первых, авторы изучили доступные источники по современным тенденциям в преподавании теории вероятностей и выбрали те из них, которые близки авторской концепции формирования у студентов вероятностного подхода к познанию [8].
Таким образом, авторы дают дополнительную аргументацию по необходимости переакцентировки преподавания курса теории вероятностей и математической статистики, который должен соответствовать не только историческому пути развития этой науки, но и современным задачам практической деятельности.
Во-вторых, авторы проводят численное исследование решений некоторых задач теории вероятностей, сравнивая точность моделей, основанных на схеме Бернулли, формуле Пуассона и интегральной теореме Лапласа. При этом на основании визуального графического анализа авторам удалось сформировать некоторые рекомендации по наглядному представлению студентам положений о точности вероятностных моделей. Кроме того, было проведено статистическое исследование погрешностей анализируемых моделей.
Результаты исследования и их обсуждение
Вопросы развития у студентов представлений о точности вероятностных моделей заинтересовали авторов в связи с развиваемой ими концепцией формирования вероятностного подхода к познанию [8]. В этой области существуют, видимо, независимые исследования ряда вузовских ученых. Прежде всего это публикации, группирующиеся вокруг Г.Д. Гефана [9], в том числе развивающие понятие «вероятностный стиль мышления» [10], близкое по смыслу к понятию «вероятностный подход», используемому авторами. Далее следует отметить работы М.Э. Григорян и ее соавторов [11], также связанные с формированием научного мировоззрения студентов через вероятностную картину мира [12]. Наконец, в вышедшей недавно работе Т.В. Васильева приводит примеры практических заданий, способствующих повышению стохастической культуры обучающихся [13].
Вероятностный подход к познанию, вероятностный стиль мышления, вероятностная картина мира и стохастическая культура с разных сторон и в разных измерениях подтверждают необходимость формирования у студентов компетенций в области теории вероятности, опираясь на которые, они смогут в профессиональной деятельности строить адекватные модели анализируемых процессов и явлений, принимая во внимание не только детерминистские, но и стохастические факторы.
Проблема точности вероятностных моделей является одним из компонентов вероятностного подхода, которому в преподавании, в том числе и авторами, уделяется недостаточное внимание. Разумеется, инженеры и экономисты забудут о методах оценки точности, даже если бы они изучали их на 2-м курсе, но само представление о необходимости такой оценки должно входить в компетентностную модель выпускника.
Авторы предлагают ряд примеров, которые можно демонстрировать студентам для иллюстрации положений о точности вероятностных моделей.
Задание 1. 25% проектов фирмы – крупные. Случайная величина (СВ) Х – число крупных проектов. Построить полигон – график ряда распределения СВ Х, если фирма выполняет n проектов для следующих случаев: 1) n = 5: 2) n = 10; 3) n = 15; 4) n = 20.
Решение: значения параметров:
.
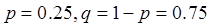Используя формулу Бернулли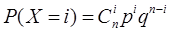 
, получаем графики (рис. 1).
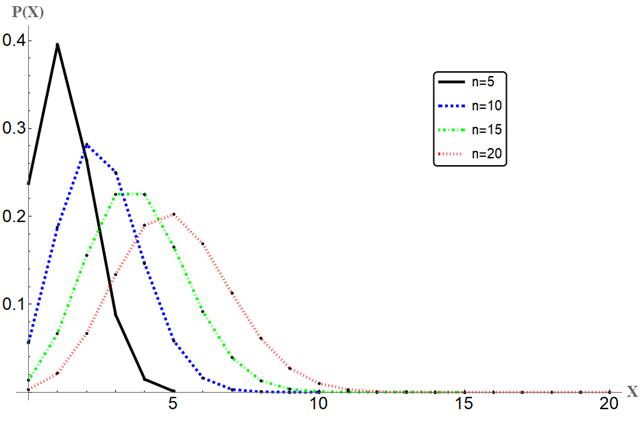
Рис. 1. Полигоны распределения по схеме Бернулли при р = 0,25
Величина р = 0,25 была выбрана для демонстрации несимметричности распределения Бернулли. Очень часто для иллюстрации схемы Бернулли выбирают р = 0,5, и у студентов может сложиться ошибочное мнение о симметричном характере распределения.
Дидактический вывод по Заданию 1: с ростом числа испытаний полигон распределения Бернулли приближается к дискретному аналогу нормального распределения. Это свидетельствует в пользу замены расчета по точной формуле Бернулли приближенным расчетом по теореме Лапласа.
Задание 2. 25% проектов фирмы – крупные. Случайная величина (СВ) Х – число крупных проектов. Найти по формуле Бернулли и теореме Лапласа 1) P (4 ≤ X ≤ 6 при n = 20; 2) P (46 ≤ X ≤ 54) при n = 200; 3) P (486 ≤ X ≤ 514) при n = 2000.
Решение:
1) n = 20; P (4 ≤ X ≤ 6)
· по формуле Бернулли:
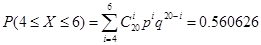
· по теореме Лапласа:
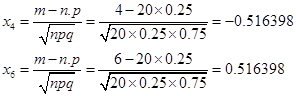
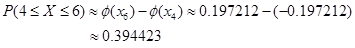
Здесь далее Φ – значение нормированной функции Лапласа.
2) n = 200; P (46 ≤ X ≤ 54)
· по формуле Бернулли:
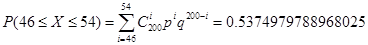
· по теореме Лапласа:
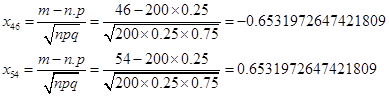
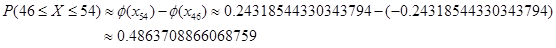
3) n = 2000; P (486 ≤ X ≤ 514)
· по формуле Бернулли:
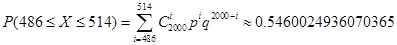
· по теореме Лапласа:
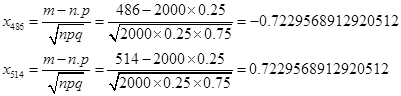
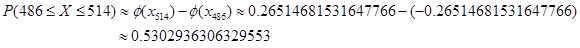
Границы интервалов были выбраны на основании данных предварительного анализа таким образом, чтобы величины интервальной вероятности, вычисленной по формуле Бернулли PB, были бы максимально близкими. Для того чтобы оценить погрешность результатов, полученных по приближенной формуле Лапласа PL, по сравнению с точной формулой Бернулли PB, были вычислены абсолютная ошибка Δ = PB – PL и относительная ошибка ε = Δ / PB (табл.).
Абсолютная и относительная ошибки значений вероятности
по формуле Бернулли и по теореме Лапласа
|
n |
Δ |
ε |
ε (%) |
|
20 |
|
|
29,6% |
|
200 |
|
|
9,5% |
|
2000 |
|
|
2,8% |
Графики относительной ошибки и ее возможных аппроксимаций приведены на рисунке 2, где по горизонтальной оси введена логарифмическая шкала.
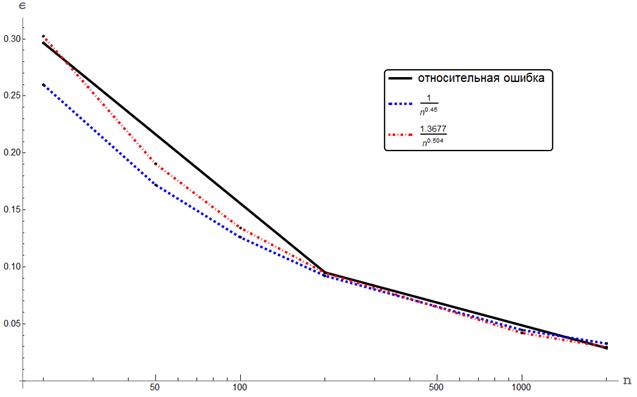
Рис. 2. Относительная ошибка вычисления вероятности по формуле Бернулли и по теореме Лапласа и ее возможные аппроксимации
идно, что относительная ошибка уменьшается с ростом числа опытов. Характер убывания – обратный корневому, что согласуется с положениями теории погрешностей С.Г. Михлина.
Дидактический вывод по Заданию 2: с ростом числа испытаний растет точность вычислений значений интервальной вероятности по приближениям, опирающимся на интегральную теорему Лапласа. Это подтверждает визуальный вывод, который был сделан на основании выполнения Задания 1. В то же время даже при большом числе опытов значение относительной ошибки величиной около 3% нельзя назвать удовлетворительным. Это значит, что пользоваться теоремой Лапласа вместо формулы Бернулли предпочтительнее для предварительного или качественного оценивания.
Задание 3. 1% проектов фирмы – крупные. Случайная величина (СВ) Х – число крупных проектов. Построить полигон – график ряда распределения СВ Х, если фирма выполняет проекты по формуле Бернулли и по формуле Пуассона для 1) n = 20; 2) n = 200.
Решение: значения параметров:
.
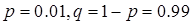Очевидно, что событие «крупный проект» можно считать редким. Используя точную формулу Бернулли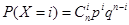 
и приближенную формулу Пуассона 
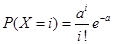, где 
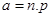, получаем графики полигонов распределения (рис. 3).
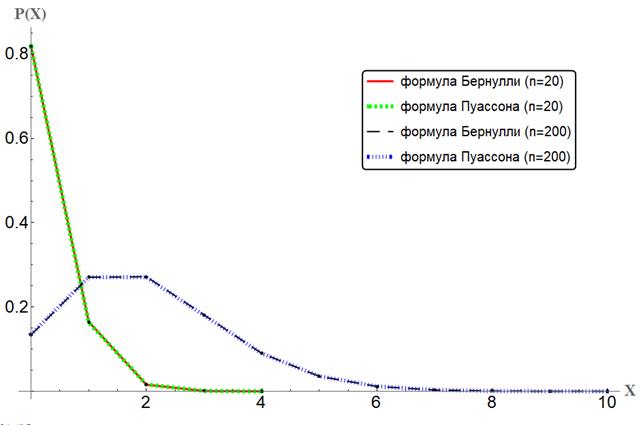
Рис. 3. Полигоны распределения числа редких событий
Дидактический вывод по Заданию 3: на основании числовых и визуальных данных можно констатировать, что вероятности редких событий (р = 0,1), вычисленные по точной формуле Бернулли и по приближенной формуле Пуассона, практически не различаются. Значит, для значений вероятности редкого события р ≤ 0,1 можно рекомендовать использование приближенной формулы Пуассона.
Задание 4. 1% проектов фирмы – крупные. Случайная величина (СВ) Х – число крупных проектов. Найти по формуле Бернулли, по формуле Пуассона и по теореме Лапласа 1) P (9 ≤ X ≤ 11) при n=100; 2) P (90 ≤ X ≤ 10) при n = 1000.
Решение:
1) n = 100; P (9 ≤ X ≤ 11)
· по формуле Бернулли
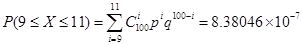
· по формуле Пуассона
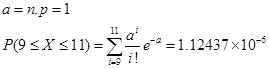
· по теореме Лапласа
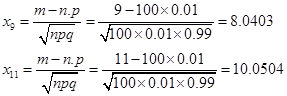
Обычно при х > 5 принимают значение функции Лапласа равным 0,5. Вычислив с большей точностью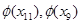 
, получаем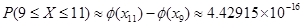 
2) n = 1000; P (90 ≤ X ≤ 110)
· по формуле Бернулли:
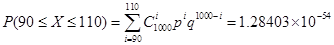
· по формуле Пуассона:
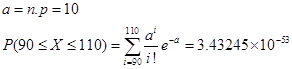
· по теореме Лапласа:
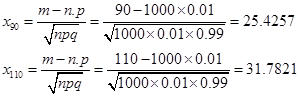
Обычно при х > 5 принимают значение функции Лапласа равным 0,5. Вычислив с большей точностью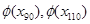 
, получаем
.
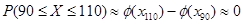Дидактический вывод по Заданию 4: оценивание интервальной вероятности для редкого события (р = 0,1) по точной формуле Бернулли и по приближенной формуле Пуассона или по приближенной интегральной теореме Лапласа дает сходные результаты, отличающиеся в 6-м знаке после запятой и дальше. Значит, для интервальных значений вероятности редкого события р ≤ 0,1 можно рекомендовать использование приближенной теоремы Лапласа, требующей минимума вычислительной работы.
Выводы
Авторами предложены варианты заданий, выполнение которых способствует формированию у обучающихся вероятностного подхода к познанию в части оценки точности вероятностных моделей. Несмотря на то что в отечественной средней школе изучаются основы теории вероятности, студенты 1–2-х курсов оказываются мало подготовленными к восприятию информации, связанной с построением вероятностных моделей явлений окружающего мира. С большим интересом и пониманием рассмотрение этих вопросов было встречено в аудитории иностранных обучающихся, готовящихся к поступлению в магистратуру [14, 15]. Это приводит к мысли о том, что организация программ предмагистерской подготовки была бы полезной для формирования качественного контингента магистратуры инженерных и экономических направлений подготовки.
Библиографическая ссылка
Краснощеков В.В., Семенова Н.В., Алдармини С.С. МЕТОДЫ ФОРМИРОВАНИЯ КОМПЕТЕНЦИЙ СТУДЕНТОВ В ОБЛАСТИ ТОЧНОСТИ ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ // Современные проблемы науки и образования. – 2020. – № 5. ;URL: https://science-education.ru/ru/article/view?id=30142 (дата обращения: 24.04.2024).