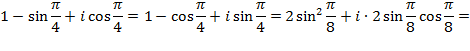Понятие числа - одно из основных понятий математики. Исторически первым было понятие натурального числа, которое сложилось в процессе счета предметов и являлось количественной стороной событий. Но уже простейшие практические задачи, связанные с измерением, привели к расширению понятия числа – появилось понятие дробного (рационального положительного) числа. При помощи рациональных чисел с любой наперед заданной точностью можно осуществить практически любые измерения. К действительным числам привело математическое открытие, возникающее из теоремы Пифагора и заключающееся в том, что длина диагонали единичного квадрата не может быть выражена точно рациональным числом. Последовательное изучение чисел в школе во многом повторяет эту историческую последовательность появления чисел: натуральные числа, дроби (положительные), целые числа, рациональные числа, иррациональные и действительные. На этом общеобразовательная программа по математике ставит точку, но развитие понятия числа на этом не остановилось. Внутренние потребности математики привели к комплексным числам (а в дальнейшем уже и к их обобщению). Таким образом, более логически правильным было бы заканчивать изучение понятия числа в школе именно темой «Комплексные числа». Тем более в нашей истории математического образования были периоды, когда эта тема входила в программы по математике старшей школы. Начиная c 1917 года в советских школах изучались чисто мнимые числа, спустя пять лет, т.е. с 1932 года, в программу 8 класса включается тема «Комплексные числа», которая изучается до окончания школьного курса математики. Но с 1968 года, в результате модернизации общеобразовательного курса математики, раздел «Комплексные числа» в обычных классах не рассматривается, только в профильных. Следует также отметить, что комплексные числа важны как область математики, в которой замечательно работают знания и умения, полученные обучающимися при изучении алгебры и тригонометрии.
Цель исследования: обосновать необходимость изучения комплексных чисел в курсе алгебры и начал математического анализа и определить их место в школьном курсе математики, а также рассмотреть различные задачи, которые можно решить с помощью комплексных чисел.
Материалы и методы исследования. Комплексные числа на сегодняшний день изучаются в старшей школе только в профильных классах. Как правило, согласно имеющимся УМК по алгебре и началам анализа для углубленного (профильного) изучения, тема «Комплексные числа» рассматривается в 11 классе. Это УМК, созданные под руководством Виленкина Н.Я. [1], Колягина Ю.М. [2], Пратусевич М.Я. [3], Муравина Г.К. [4], Никольского С.М. [5]. А вот в УМК, созданном под руководством Мордковича А.Г. [6], данная тема рассматривается в 10 классе.
В каждом из рассматриваемых УМК прослеживается разный подход к подведению к теме. Например, в учебнике Виленкина Н.Я. в качестве мотивации изучения комплексных чисел приводится необходимость расширения знания темы корней квадратного уравнения при 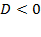 . Колягин Ю.М. обосновывает необходимость появления комплексных чисел и их изучения стремлением сделать алгебраические уравнения решаемыми для решения задач физики, практики и т.п. В УМК Муравина Г.К. поднимается проблема невозможности извлечения корней четных степеней из отрицательных чисел, и решить эту проблему может самое широкое числовое множество – множество комплексных чисел. Мордкович А.Г. в качестве подведения к изучаемой теме рассматривает проблему необходимости расширения прямой действительных чисел до поля комплексных чисел в связи с тем, что не все алгебраические операции могут выполняться на поле действительных чисел. А Пратусевич М.Я. начинает рассмотрение темы «Комплексные числа» с введения в исторический факт решения Кардано кубического уравнения.
. Колягин Ю.М. обосновывает необходимость появления комплексных чисел и их изучения стремлением сделать алгебраические уравнения решаемыми для решения задач физики, практики и т.п. В УМК Муравина Г.К. поднимается проблема невозможности извлечения корней четных степеней из отрицательных чисел, и решить эту проблему может самое широкое числовое множество – множество комплексных чисел. Мордкович А.Г. в качестве подведения к изучаемой теме рассматривает проблему необходимости расширения прямой действительных чисел до поля комплексных чисел в связи с тем, что не все алгебраические операции могут выполняться на поле действительных чисел. А Пратусевич М.Я. начинает рассмотрение темы «Комплексные числа» с введения в исторический факт решения Кардано кубического уравнения.
Результаты исследования и обсуждение. Анализ тематического планирования существующих УМК по алгебре и началам анализа показал, что при изучении главы «Комплексные числа» основными темами являются следующие:
- алгебраическая форма комплексного числа (определение комплексных чисел);
- операции над комплексными числами (сложение, вычитание, умножение, деление);
- комплексные числа и координатная плоскость (геометрическая интерпретация комплексного числа);
- тригонометрическая форма записи комплексного числа;
- комплексные числа и квадратные уравнения;
- возведение комплексного числа в степень;
- извлечение кубического корня из комплексного числа.
Отметим также, что, например, в УМК, разработанном под руководством Никольского С.М., нежели, например, в УМК Мордковича А.Г., каждая тема представлена кратко, но достаточно ёмко; имеется достаточное количество заданий для отработки необходимых умений и навыков. В УМК Мордковича А.Г. темы также раскрыты достаточно полно, но имеется излишняя вводная часть, которую где-то можно было бы сократить.
Рассмотрим примеры заданий, которые можно предложить учащимся для формирования навыков (переход от одной формы записи к другой форме; использование техники решения задач; использование простейших приёмов применения арифметических операций над комплексными числами; использование справочных материалов для нахождения нужных формул и их применения при решении задач) при изучении темы «Комплексные числа», а также для проверки знаний по данной теме. Отметим, что все полученные ранее в средней школе знания и умения необходимы и при изучении рассматриваемой темы (например, умение решать квадратные уравнения).
Задача 1. Решить уравнения: а) 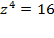 ; б)
; б) 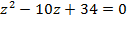 [6].
[6].
Решение. а) Перенесем все слагаемые в левую часть и разложим ее на множители: 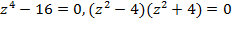 . Рассмотрим отдельно каждый множитель:
. Рассмотрим отдельно каждый множитель: 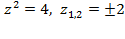 ;
; 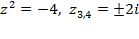 .
.
Ответ. 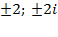 .
.
б) Найдем дискриминант уравнения: 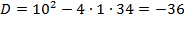 . Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:
. Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта: 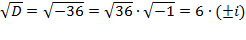 . Теперь подставляем значение дискриминанта в формулу корней квадратного уравнения:
. Теперь подставляем значение дискриминанта в формулу корней квадратного уравнения: 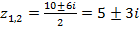 .
.
Ответ. 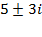 .
.
Задача 2. Найдите a и b, если 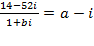 [7].
[7].
Решение. Домножим числитель и знаменатель на число 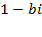 , сопряженное со знаменателем:
, сопряженное со знаменателем:
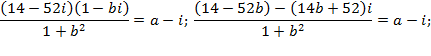
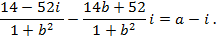
Приравнивая отдельно вещественные и мнимые части, получим
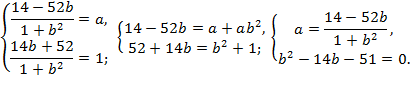
Решаем квадратное уравнение и находим
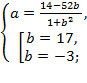
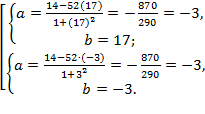
Ответ. 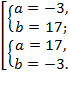
По разделу «Тригонометрическая форма записи комплексного числа» можно предложить стандартные задания, например:
Задача 3. Выполните действия:
а) 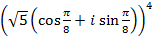 ; б)
; б) 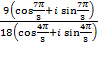 [2].
[2].
А можно предложить и более сложные задания.
Задача 4. Выполните действия 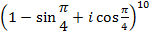 [7].
[7].
Решение. Выражение 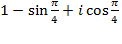 не является тригонометрической формой комплексного числа. Пользуясь формулами
не является тригонометрической формой комплексного числа. Пользуясь формулами 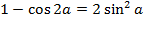 и тем, что
и тем, что 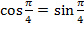 , получим
, получим
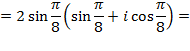
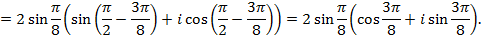
Теперь можно воспользоваться формулой Муавра:
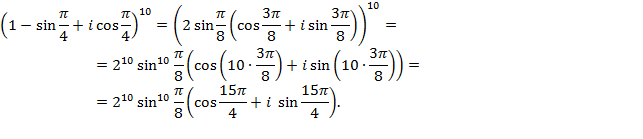
Отдельно вычислим 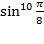 :
:
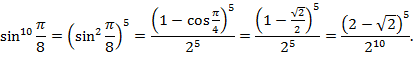
Выражение 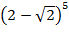 можно вычислить, используя формулу бинома Ньютона:
можно вычислить, используя формулу бинома Ньютона:
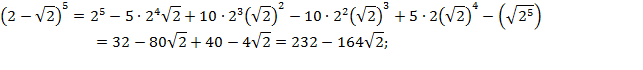
Окончательно получаем:
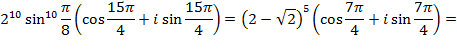
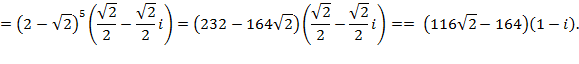
Хотелось бы отметить, что при изучении последнего расширения понятия числа часто упускается одно из главных достоинств комплексных чисел – простота решения геометрических задач методом комплексных чисел. Проанализировав учебно-методическую литературу и методику изучения темы «Геометрическая интерпретация комплексного числа», можно заметить, что при изучении данной темы рассматривается только непосредственное представление комплексных чисел на координатной плоскости, а также действия над комплексными числами на координатной плоскости: сложение и вычитание векторов, умножение вектора на число. Ни в одном из рассмотренных УМК не говорится о том, что комплексные числа позволяют иногда решать различные геометрические задачи проще, чем это можно сделать с использованием традиционных геометрических методов. Процесс решения упрощается за счет того, что в алгебре комплексных чисел имеются готовые формулы для выражения отношений геометрических фигур, и учащемуся уже не нужно тратить много времени на размышления о способе решения рассматриваемой задачи. Рассмотрим пример задачи, которую решим двумя способами: стандартным способом, т.е. с применением теорем геометрии, и методом комплексных чисел.
Задача 5. Докажите, что сумма квадратов медиан треугольника равна 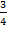 суммы квадратов его сторон.
суммы квадратов его сторон.
Решение. Чтобы решить задачу стандартным способом, учащемуся необходимо вывести формулы нахождения каждой медианы треугольника. Покажем вывод искомой формулы на примере одной из медиан.
1) Рассмотрим 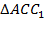 : по теореме косинусов имеем, что
: по теореме косинусов имеем, что 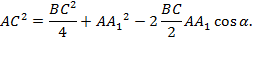
2) Рассмотрим 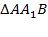 :
:
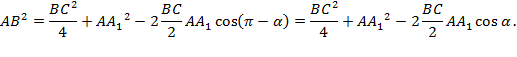
Из 1) и 2) получаем: 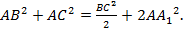 Преобразовав наше выражение и выразив медиану
Преобразовав наше выражение и выразив медиану 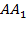 , получим формулу первой медианы:
, получим формулу первой медианы: 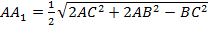 .
.
Аналогично получаем формулы для нахождения двух оставшихся медиан:
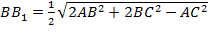 ,
, 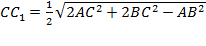 .
.
Согласно условию задачи найдем сумму квадратов медиан треугольника и получим:
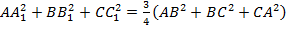 , что и требовалось доказать.
, что и требовалось доказать.
Рассмотрим теперь решение данной задачи методом комплексных чисел. Отметим, что для решения задачи вторым способом учащемуся необходимо знание всего одной формулы – формула нахождения расстояния между двумя точками, которая выглядит следующим образом: 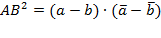 [8].
[8].
Используя формулу нахождения расстояния между двумя точками, запишем квадраты медиан треугольника:
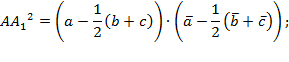
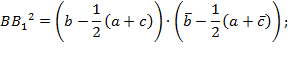
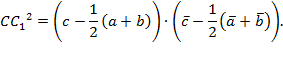
Тогда сумма квадратов медиан треугольника равна:
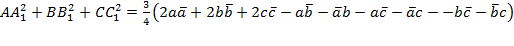 .
.
Найдем сумму квадратов сторон треугольника:
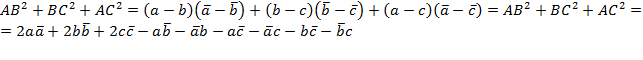 .
.
Преобразовав полученные суммы, получим: 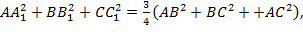 что и требовалось доказать.
что и требовалось доказать.
Кроме того, комплексные числа – это математический аппарат для описания движений плоскости. Подробнее с этим можно познакомиться в [9].
С помощью формулы Муавра возведения комплексного числа в целочисленную степень можно выводить формулы косинуса и синуса любого кратного угла, в частности двойного и тройного углов. Рассмотрим вывод формулы косинуса и синуса двойного углов.
Возьмем комплексное число
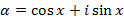
и возведем его во вторую степень, пользуясь формулой Муавра и формулой сокращенного умножения (частный случай формулы бинома Ньютона).
Получим: с одной стороны,
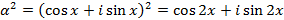 ;
;
с другой стороны,
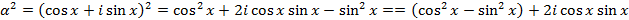
Отсюда, приравнивая отдельно действительные и мнимые части, получаем, что 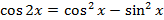 ,
, 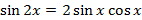 .
.
Заключение. Итак, комплексные числа – это числа, которые нашли многочисленные, а порой и неожиданные применения. Нельзя не отметить, что при решении задач с применением комплексных чисел порой обнаруживаются новые интересные факты и обобщения.
Применение метода комплексных чисел при решении задач по элементарной геометрии дает учащимся возможность научиться решать геометрические задачи аналитическим способом, не прибегая к построению чертежа.
Библиографическая ссылка
Войтенко Т.Ю., Цыганкова А.С. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ТЕМЫ «КОМПЛЕКСНЫЕ ЧИСЛА» В ПРОФИЛЬНЫХ КЛАССАХ СТАРШЕЙ ШКОЛЫ // Современные проблемы науки и образования. 2019. № 4. ;URL: https://science-education.ru/ru/article/view?id=29137 (дата обращения: 05.03.2026).