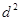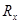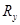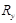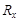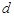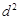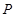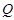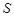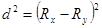Учитывая, что математика является «одной из важнейших составляющих мирового научно-технического прогресса», и ту роль, которую играет математика в науке, культуре и общественной жизни, как отмечается в принятой правительством РФ «Концепции развития математического образования в Российской Федерации», исследования по данной проблеме имеют особую актуальность и значимость. Кроме того, как отмечается в данном документе, «качественное математическое образование необходимо каждому для его успешной жизни в современном обществе» [1; 2].
Исследование результатов обучения в вузе и выбор методов для получения количественной оценки исследуемых процессов являются очень важными в педагогической теории и практике. Большое число факторов, влияющих на педагогический процесс в вузе, приводят к тому, что образование нельзя рассматривать только как детерминированный процесс. Результаты обучения студента невозможно спрогнозировать даже при очень хорошей организации учебного процесса. В таких случаях для исследования результатов обучения в вузе следует применять статистические методы. Использование методов математической статистики дает возможность получить количественные оценки исследуемых процессов, выявить связь различных составляющих процесса обучения.
Следовательно, в исследовании большую актуальность приобретает выбор методов для оценки тесноты связи между рассматриваемыми факторами процесса.
Для проверки предположений авторами в статье используются непараметрические методы корреляции, а именно коэффициенты Спирмена и Кендалла. Существенных отличий между этими коэффициентами нет, но коэффициент Кендалла дает более полную и детальную картину анализируемой связи между признаками, а коэффициент Спирмена точнее объясняет количественную связь между ними.
Преподаватели высшей школы при обучении студентов математике сталкиваются с рядом проблем. Это сокращение количества лекционных и практических занятий в связи с переходом на новые стандарты обучения, постоянно увеличивающийся разрыв между уровнем преподавания математики в вузе и знаниями, полученными обучающимися в школе.
Тем не менее преподаватели должны обеспечить должный уровень математической подготовки, что необходимо для развития навыков алгоритмического и абстрактного мышления, формализации и моделирования ситуации, решения практических задач. Изучение математики является базой качественного технического образования, в том числе для студентов экономических специальностей.
В исследовании авторы оценивают тесноту связи между успеваемостью по нематематическим и математическим дисциплинам по результатам зимней и летней сессии студентов Института экономики и управления АлтГТУ им. И.И. Ползунова за 2017-2018 учебный год.
В качестве методов исследования были выбраны непараметрические методы корреляции рангов.
Особенностям преподавания математики студентам вузов посвящен ряд работ [3-5]. Большинство авторов обсуждают математические знания первокурсников, формирование программ обучения математике в вузе, практическую направленность обучения математике [3; 4]. Например, Колбина Е.В. исследует повышение мотивации студента, позволяющей активизировать его деятельность [4]. Обсуждаются предметные связи математики с другими дисциплинами, профессионально ориентированные задачи. В том числе авторов интересуют проблемы плохого понимания студентами абстрактных математических моделей, как говорит Tim Tarver: «Язык математики не понятен многим студентам» [5].
В работах также выделяется множество причин плохой успеваемости по математическим дисциплинам студентов-гуманитариев. Это слабая школьная подготовка (формирование в школе «гуманитарных» классов, в результате чего студенты относятся негативно к изучению данной дисциплины в вузе [6]), слабая мотивация студентов, связанная с общественной недооценкой значимости математического обучения [7], недостаточно осознанный выбор профессионального направления при поступлении в вуз [8]. Кроме того, подавляющее большинство вариантов программ по математике для гуманитарных классов составляются с сокращением объема (и часов) классических общеобразовательных программ по математике [9].
Авторами для исследования качества успеваемости студентов по математике предложено использовать коэффициенты ранговой корреляции [10]. Как правило, непараметрические методы статистики чаще используются в медицинских исследованиях, поскольку при описании данных используются как количественные, так и качественные характеристики [11]. Однако авторы используют эти методы математической статистики в своей работе, так как они позволяют оценить полученные данные с выборкой небольшого объема.
Таким образом, несмотря на достаточную изученность проблемы математического обучения в вузах в целом, использование непараметрических методов исследования в приложении к преподаванию математики, на наш взгляд, недостаточно изучено.
В статье авторы рассматривают недостаточно изученный вопрос успеваемости по математике студентов гуманитарных направлений - так называемую проблему гуманитарного склада ума, исследуя успеваемость студентов экономических специальностей технического вуза, которые значительно отличаются по уровню и качеству математической подготовки от студентов технических направлений. Поэтому преподаватели вынуждены на занятиях находить время для восполнения недостатка недостающих знаний по математике. В результате студенты с сильной математической подготовкой в школе «скучают» на занятиях в вузе, а слабые утверждают, что математика – это не их сильная сторона, что у них так называемый гуманитарный склад ума [10].
Цель исследования - опровергнуть вышеназванное предположение о так называемом гуманитарном складе ума.
Задача исследования - выявить зависимость успеваемости студентов по математике от результатов обучения по другим дисциплинам.
Научная новизна проведенного авторами исследования заключается в том, что на примере студентов Института экономики и управления АлтГТУ им. И.И. Ползунова впервые показано, что успеваемость по математическим дисциплинам является довольно значимым критерием для прогнозирования успешности обучения. Выявлено наличие существенной прямой связи между успеваемостью по математике и другим дисциплинам.
Задача оценки тесноты связи двух альтернативных качественных признаков, а именно успеваемости по математике и другим дисциплинам, впервые решена непараметрическими методами корреляции.
Материалы и методы исследования
На первом этапе исследования рассмотрены результаты зимней сессии студентов первого курса направления «Менеджмент» Института экономики и управления АлтГТУ им. И.И. Ползунова, выбранные в качестве объекта исследования.
Для оценки тесноты связи двух альтернативных качественных признаков, а именно успеваемости по математике и по другим дисциплинам, рассчитаны ранговые коэффициенты корреляции Спирмена и Кендалла, позволяющие упорядочить (ранжировать) объекты анализа по степени выраженности измеряемых признаков. Для вычисления коэффициентов данные ранжируются по значению качественных или количественных признаков. При этом каждому объекту присваивается определенный номер (ранг).
При ранжировании объектов по двум признакам тесноту связи между признаками можно оценить с помощью коэффициента ранговой корреляции Спирмена r, выполнив следующие действия:
1) варианты факторного признака (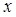 ) расположить по возрастанию (убыванию) – ранжировать по значению признака;
) расположить по возрастанию (убыванию) – ранжировать по значению признака;
2) для каждой единицы совокупности указать ранг с точки зрения результативного признака (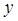 );
);
3) вычислить коэффициент ранговый корреляции (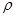 ) по формуле:
) по формуле:
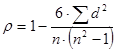 ,
,
где 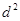 - квадраты разности рангов между факторным и результативным признаками для каждой единицы совокупности;
- квадраты разности рангов между факторным и результативным признаками для каждой единицы совокупности; 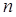 - число наблюдений [11].
- число наблюдений [11].
Чтобы оценить полученный результат, необходимо для проведения «грубого» контроля вспомнить о том, что область определения коэффициентов корреляции всех видов (линейная корреляция, множественная корреляция и др.) располагается от -1 до +1 [12]. Учитывая вышесказанное, можно будет сделать вывод о наличии либо прямой связи между изучаемыми признаками, либо обратной, либо о ее отсутствии. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между изучаемыми признаками. Связь считается статистически значимой, если значение коэффициента 
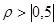 .
.
Вычисление рангового коэффициента корреляции Кендалла (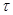 ) происходит в несколько этапов:
) происходит в несколько этапов:
1) значения факторного признака х ранжируются в порядке возрастания (или убывания) с указанием соответствующих им рангов по признаку у;
2) для каждого наблюдения подсчитывается Р – число случаев, когда ранг признака y у следующих наблюдений меньше, чем у данного;
3) для каждого наблюдения подсчитывается Q – число случаев, когда у следующих наблюдений ранг результативного признака у больше, чем у данного;
4) определяется сумма баллов 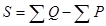 ;
;
5) рассчитывается коэффициент Кендалла по формуле:
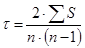
Связь между признаками признается статистически значимой, если коэффициент ранговой корреляции Кендалла 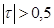 . Коэффициент Кендалла можно также использовать в многофакторном анализе, в отличие от коэффициента Спирмена [13].
. Коэффициент Кендалла можно также использовать в многофакторном анализе, в отличие от коэффициента Спирмена [13].
По результатам зимней сессии студентов первого курса специальности «Менеджмент» был вычислен средний балл по всем изучаемым дисциплинам, кроме математики. Данные проранжированы в порядке убывания и рассчитан ранг рейтинга успеваемости студента Ry. Результаты успеваемости по математике были также упорядочены в порядке убывания, и вычислен ранг Rx (таблица 1).
При этом если значения рейтинга имели одинаковую количественную оценку, то их ранг принимался равным средней арифметической соответствующих номеров их мест.
В таблице 1 приведены результаты расчета коэффициентов корреляции рангов Спирмена и Кендалла.
Таблица 1
Расчет коэффициентов корреляции рангов Спирмена и Кендалла
|
Учащиеся |
Ранги |
d |
|
P |
Q |
S |
|
|
|
|
||||||
|
Ж |
1,00 |
4,00 |
-3,00 |
9,00 |
3 |
13 |
10 |
|
В |
3,50 |
3,00 |
0,50 |
0,25 |
2 |
13 |
11 |
|
З |
3,50 |
5,00 |
-1,50 |
2,25 |
2 |
12 |
10 |
|
Н |
3,50 |
6,00 |
-2,50 |
6,25 |
2 |
11 |
9 |
|
С |
3,50 |
9,00 |
-5,50 |
30,25 |
4 |
8 |
4 |
|
Л |
6,00 |
2,00 |
4,00 |
16,00 |
1 |
10 |
9 |
|
Е |
8,00 |
1,00 |
7,00 |
49,00 |
0 |
10 |
10 |
|
О |
8,00 |
13,50 |
-5,50 |
30,25 |
5 |
3 |
-2 |
|
Р |
8,00 |
12,00 |
-4,00 |
16,00 |
4 |
4 |
0 |
|
М |
10,50 |
10,50 |
0,00 |
0,00 |
2 |
4 |
2 |
|
П |
10,50 |
7,50 |
3,00 |
9,00 |
0 |
5 |
5 |
|
Д |
12,50 |
13,50 |
-1,00 |
1,00 |
2 |
3 |
1 |
|
И |
12,50 |
7,50 |
5,00 |
25,00 |
0 |
4 |
4 |
|
К |
14,00 |
10,50 |
3,50 |
12,25 |
0 |
3 |
3 |
|
Г |
15,00 |
15,50 |
-0,50 |
0,25 |
0 |
1 |
1 |
|
А |
16,50 |
15,50 |
1,00 |
1,00 |
0 |
1 |
1 |
|
Б |
16,50 |
17,00 |
-0,50 |
0,25 |
0 |
0 |
0 |
|
ИТОГО |
208 |
27 |
105 |
78 |
|||
Вычислив коэффициент корреляции Спирмена для 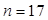 :
:
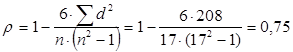 ,
,
видим, что полученное значение коэффициента 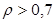 , что свидетельствует o наличии прямой и сильной связи между успешной сдачей экзамена по математике студентом и его успеваемостью по другим дисциплинам.
, что свидетельствует o наличии прямой и сильной связи между успешной сдачей экзамена по математике студентом и его успеваемостью по другим дисциплинам.
Проверим значимость найденного коэффициента 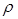 , применив
, применив 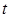 - распределение Стьюдента на уровне значимости
- распределение Стьюдента на уровне значимости  с числом степеней свободы
с числом степеней свободы 
Вычислим 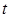 - фактическое [13]:
- фактическое [13]:
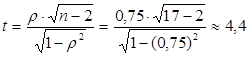
и найдем 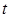 - табличное, т.е.
- табличное, т.е. 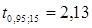 . Так как
. Так как 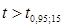 , следовательно, связь между успеваемостью по математике и успеваемостью по другим предметам статистически значима.
, следовательно, связь между успеваемостью по математике и успеваемостью по другим предметам статистически значима.
Рассчитав коэффициент ранговой корреляции Кендалла 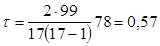 , мы убеждаемся, что связь между признаками признается статистически значимой, так как значение коэффициента
, мы убеждаемся, что связь между признаками признается статистически значимой, так как значение коэффициента 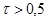 .
.
Следовательно, рассчитанные коэффициенты Спирмена и Кендалла подтверждают наличие существенной прямой связи между качеством успеваемости по естественно-научным дисциплинам и по гуманитарным предметам. То есть если обучающийся успешно освоил такую дисциплину, как, например, математика, то и по иностранному языку он также будет успешен.
Рассмотрим вопрос шире и исследуем результаты летней сессии 2017-2018 учебного года студентов первого и второго курса Института экономики и управления (ИЭиУ). В качестве объекта исследования выберем направления обучения: 38.03.02 - «Менеджмент», 38.03.04 – «Государственное и муниципальное управление», 38.03.01 - «Экономика», а также 38.05.01 – «Экономическая безопасность».
В ИЭиУ на первом курсе обучается 112 студентов, в том числе по направлению «Менеджмент» – 16, «Экономика» – 22, «Государственное и муниципальное управление» – 19, «Экономическая безопасность» – 55.
На примере результатов летней сессии 2018 года у студентов направления «Экономика» покажем расчет ранговых коэффициентов корреляции Спирмена и Кендалла.
В таблице 2 приведены: комплексный рейтинг студента (без математики); рейтинг по математике, упорядоченный от максимального значения к минимальному, а также вычислены ранги рейтинга успеваемости студента Ry и ранг Rx. При этом если значения рейтинга имели одинаковую количественную оценку, то ранг принимался равным средней арифметической соответствующих номеров их мест.
Таблица 2
Результаты успеваемости студентов первого курса направления «Экономика»
|
Учащиеся |
Комплексный рейтинг |
Математика |
Учащиеся |
Комплексный рейтинг |
|
Учащиеся |
Математика |
|
|
||
|
A |
79 |
43 |
A |
79 |
1 |
Х |
75 |
1 |
16,5 |
||
|
Б |
67 |
38 |
Д |
78 |
2 |
В |
63 |
2 |
3,5 |
||
|
В |
76 |
63 |
В |
76 |
3,5 |
И |
60 |
3,5 |
8,5 |
||
|
Г |
72 |
53 |
З |
76 |
3,5 |
Л |
60 |
3,5 |
10,5 |
||
|
Д |
78 |
43 |
К |
73 |
5 |
Ж |
56 |
5 |
3,5 |
||
|
Е |
60 |
50 |
Г |
72 |
6 |
К |
55 |
6 |
5 |
||
|
Ж |
49 |
25 |
Б |
67 |
7 |
Г |
53 |
7 |
6 |
||
|
З |
76 |
56 |
И |
66 |
8,5 |
Е |
50 |
8 |
13 |
||
|
И |
66 |
60 |
М |
66 |
8,5 |
М |
47 |
9 |
8,5 |
||
|
К |
73 |
55 |
Л |
63 |
10,5 |
A |
43 |
11 |
1 |
||
|
Л |
63 |
60 |
Р |
63 |
10,5 |
Д |
43 |
11 |
2 |
||
|
М |
66 |
47 |
У |
62 |
12 |
У |
43 |
11 |
12 |
||
|
Н |
56 |
30 |
Е |
60 |
13 |
Р |
40 |
13,5 |
10,5 |
||
|
О |
21 |
25 |
Н |
56 |
14 |
С |
40 |
13,5 |
18 |
||
|
П |
30 |
25 |
Ж |
49 |
15 |
Б |
38 |
15 |
7 |
||
|
Р |
63 |
40 |
Х |
39 |
16,5 |
Н |
30 |
16 |
14 |
||
|
С |
37 |
40 |
Ц |
39 |
16,5 |
Ж |
25 |
19,5 |
15 |
||
|
Т |
30 |
25 |
С |
37 |
18 |
О |
25 |
19,5 |
22 |
||
|
У |
62 |
43 |
П |
30 |
19,5 |
П |
25 |
19,5 |
19,5 |
||
|
Ф |
28 |
25 |
Т |
30 |
19,5 |
Т |
25 |
19,5 |
19,5 |
||
|
Х |
39 |
75 |
Ф |
28 |
21 |
Ф |
25 |
19,5 |
21 |
||
|
Ц |
39 |
25 |
О |
21 |
22 |
Ц |
25 |
19,5 |
16,5 |
Оценим тесноту связи между успеваемостью по математике и другим изучаемым дисциплинам также с помощью коэффициентов ранговой корреляции Спирмена и Кендалла (таблица 3).
Вычислив коэффициент корреляции Спирмена для 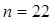 :
:
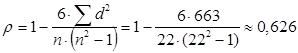 ,
,
видим, что полученное значение коэффициента Спирмена выше 0,6, что свидетельствует o наличии прямой и сильной связи между успешной сдачей экзамена по математике студентом и его успеваемостью по другим дисциплинам.
Таблица 3
Расчет коэффициентов корреляции рангов успеваемости студентов первого курса направления «Экономика» по математике и другим изучаемым дисциплинам
|
Учащиеся |
|
|
|
|
|
|
|
|||
|
Х |
1 |
16,5 |
-15,5 |
240,25 |
16 |
5 |
-11 |
|||
|
В |
2 |
3,5 |
-1,5 |
2,25 |
2 |
18 |
16 |
|||
|
И |
3,5 |
8,5 |
-5 |
25 |
6 |
13 |
7 |
|||
|
Л |
3,5 |
10,5 |
-7 |
49 |
7 |
11 |
4 |
|||
|
З |
5 |
3,5 |
1,5 |
2,25 |
2 |
15 |
13 |
|||
|
К |
6 |
5 |
1 |
1 |
2 |
14 |
12 |
|||
|
Г |
7 |
6 |
1 |
1 |
2 |
13 |
11 |
|||
|
Е |
8 |
13 |
-5 |
25 |
6 |
8 |
2 |
|||
|
М |
9 |
8,5 |
0,5 |
0,25 |
3 |
10 |
7 |
|||
|
А |
11 |
1 |
10 |
100 |
0 |
12 |
12 |
|||
|
Д |
11 |
2 |
9 |
81 |
0 |
11 |
11 |
|||
|
У |
11 |
12 |
-1 |
1 |
2 |
8 |
6 |
|||
|
Р |
13,5 |
10,5 |
3 |
9 |
1 |
8 |
7 |
|||
|
С |
13,5 |
18 |
-4,5 |
20,25 |
4 |
4 |
0 |
|||
|
Б |
15 |
7 |
8 |
64 |
0 |
7 |
7 |
|||
|
Н |
16 |
14 |
2 |
4 |
0 |
6 |
6 |
|||
|
Ж |
19,5 |
15 |
4,5 |
20,25 |
0 |
5 |
5 |
|||
|
О |
19,5 |
22 |
-2,5 |
6,25 |
1 |
3 |
2 |
|||
|
П |
19,5 |
19,5 |
0 |
0 |
1 |
2 |
1 |
|||
|
Т |
19,5 |
19,5 |
0 |
0 |
1 |
1 |
0 |
|||
|
Ф |
19,5 |
21 |
-1,5 |
2,25 |
1 |
0 |
-1 |
|||
|
Ц |
19,5 |
16,5 |
3 |
9 |
0 |
0 |
0 |
|||
|
Сумма |
663 |
Сумма |
117 |
|
||||||
Проверим значимость найденного коэффициента 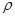 , применив
, применив 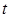 - распределение Стьюдента на уровне значимости
- распределение Стьюдента на уровне значимости 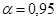 с числом степеней свободы
с числом степеней свободы 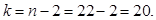
Вычислим 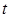 - фактическое [13]:
- фактическое [13]:
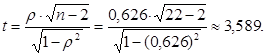
И найдем 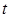 - табличное, т.е.
- табличное, т.е. 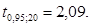
Так как 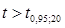 , следовательно, связь между успеваемостью по математике и успеваемостью по другим предметам статистически значима.
, следовательно, связь между успеваемостью по математике и успеваемостью по другим предметам статистически значима.
Рассчитав коэффициент ранговой корреляции Кендалла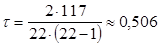 , мы еще раз убеждаемся, что связь между признаками является статистически значимой, так как значение коэффициента
, мы еще раз убеждаемся, что связь между признаками является статистически значимой, так как значение коэффициента 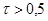 .
.
Проведем аналогичное исследование для всех студентов первого курса (таблица 4).
Таблица 4
Значения коэффициента корреляции рангов Спирмена
|
Направление обучения |
Квадраты разности рангов |
Число наблюдений |
Коэффициент Спирмена |
|
Менеджмент |
300 |
16 |
0,56 |
|
Экономика |
663 |
22 |
0,63 |
|
Государственное и муниципальное управление |
461 |
19 |
0,60 |
|
Экономическая безопасность |
9738 |
55 |
0,65 |
|
Сводная по всем студентам первого курса ИЭиУ |
109459 |
112 |
0,53 |
Студенты второго курса направлений «Экономическая безопасность» и «Экономика» изучают дисциплину «Теория вероятностей и математическая статистика». Оценим тесноту связи между успеваемостью по вышеназванной дисциплине (факторный признак - x) и другим изучаемым дисциплинам (результативный признак - y) с помощью коэффициента корреляции рангов Спирмена для 69 студентов второго курса:
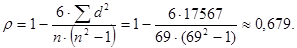
Рассчитанные коэффициенты Спирмена и Кендалла подтверждают наличие существенной прямой связи между успеваемостью по математике (в том числе и по дисциплине «Теория вероятностей и математическая статистика») и другим дисциплинам.
Полученные результаты исследования могут служить основой для решения важных проблем измерения результатов обучения в вузе, выбора методов получения количественной оценки исследуемых процессов, повышения качества подготовки студентов.
Методика оценки позволит изучить тесноту связи двух альтернативных качественных признаков, в том числе между успеваемостью по нематематическим и математическим дисциплинам.
Практическая значимость данной работы состоит в том, что используемые непараметрические методы оценки тесноты связи качественных признаков могут быть использованы при разработке учебных программ дисциплин и организации математической подготовки в вузе в целом.
А также помогут опровергнуть бытующее мнение о том, что гуманитариям математика не нужна.
Заключение
Проведенное исследование позволяет сделать следующие выводы:
- если статистическая значимость полученных результатов подтверждена непараметрическими методами математической статистики, то оценка тесноты связи двух альтернативных качественных признаков может считаться объективной;
- достоинством непараметрических методов, используемых в статье, является то, что их можно применять для исследований с выборкой небольшого объема;
- показано применение ранговой корреляции Спирмена и Кендалла к исследованию качества успеваемости студентов на примере результатов зимней и летней сессии студентов Института экономики и управления АлтГТУ им. И.И. Ползунова за 2017-2018 учебный год;
- в результате использования коэффициентов ранговой корреляции установлено, что успешный студент успешен по всем предметам, а его успеваемость зависит от мотивации и желания учиться, сформированной школьной базы, а не от того, какой у него «склад ума», что и подтверждается результатами исследования.
Авторы считают перспективным применение непараметрических методов корреляции при проведении подобных исследований у студентов технических специальностей и формирование программы по изучению математики во взаимосвязи с другими дисциплинами.
Бесспорно, что вопрос о применении в подобных исследованиях математической статистики сложен и заслуживает более детального изучения.
Библиографическая ссылка
Шарикова Т.Г., Макушева Г.Н., Шавандина О.А., Харинова О.В. ИССЛЕДОВАНИЕ ПРОБЛЕМ ОБУЧЕНИЯ В ТЕХНИЧЕСКОМ ВУЗЕ ПОСРЕДСТВОМ НЕПАРАМЕТРИЧЕСКИХ МЕТОДОВ КОРРЕЛЯЦИИ // Современные проблемы науки и образования. 2019. № 3. ;URL: https://science-education.ru/ru/article/view?id=28915 (дата обращения: 29.12.2025).