Раздел физики «Гидростатика» [1-3] на протяжении изучения всего школьного курса физики рассматривается лишь в 7 классе [4]. Этот раздел знакомит обучающихся с понятием «давление», формулирует закон Паскаля, на основе которого раскрывается принцип устройства гидравлического пресса, даёт сведения о сообщающихся сосудах и о явлении «гидростатического парадокса» [5; 6].
В ходе изложения данного раздела важной задачей для учителя является показать ученикам значимость закона Паскаля. Необходимо отметить, что этот закон является фундаментальным законом для гидростатики, поскольку он справедлив для идеальных жидкостей и газов, то есть для жидкостей и газов, у которых отсутствует внутреннее трение, то есть нет касательных напряжений между двумя соседними слоями. Особое внимание закону Паскаля нужно уделить при рассмотрении гидростатического парадокса. Этот парадокс продемонстрировал французский ученый Б. Паскаль в 1648 году, поразив своим опытом современников. В прочную, наполненную водой и закрытую со всех сторон, бочку он вставил узкую трубку и, поднявшись на балкон второго этажа дома, вылил в эту трубку кружку воды. Давление на стенки бочки так возросло, что планки (клёпки) бочки разошлись и вода из бочки стала выливаться [4].
Учащиеся 7 класса к восприятию данного явления ещё не готовы, т.к. для этого необходимо знание третьего закона Ньютона. Поэтому подробное объяснение явления гидростатического парадокса рационально включить в программу курса физики для 9 класса [7], в раздел «Законы взаимодействия тел», сразу после изучения третьего закона Ньютона. На изучение данного раздела отводится 27 академических часов. Поэтому, на наш взгляд, уместно увеличить количество академических часов, отводимых на изучение этого раздела, до 28, путём извлечения одного академического часа из числа резервных.
Всё сказанное определило поставленную цель.
Цель исследования – изложение методики объяснения гидростатического парадокса в школьном курсе физики с обоснованием рационального календарного времени его изучения.
Материал и методы исследования. В качестве материала исследования были взяты учебники физики 7 и 9 классов. Были применены следующие методы исследования: метод физического эксперимента, метод наблюдения, метод графического представления физических явлений.
Результаты исследования и их обсуждение
1. Проведен методический анализ изложения темы «Закон Паскаля» в учебниках 7 и 9 классов.
2. Разработана методика изучения темы «Закон Паскаля», представляющаяся более обоснованной и эффективной, чем в действующих учебниках.
Результаты исследования прошли апробацию 10 ноября 2017 г. на конференции «Физические модели и процессы в дисциплинах естественно-научного цикла», проведенной на факультете физики, математики, информатики Таганрогского института им. А.П. Чехова (филиал ФГБОУ ВО «Ростовский государственный экономический университет (Ростовский институт народного хозяйства)», и рекомендованы к опубликованию.
Рассмотрим более рациональную, на наш взгляд, методику объяснения явления гидростатического парадокса.
Пусть мы имеем 3 невесомых сосуда с площадью основания, равной S. Сосуды заполнены однородной идеальной жидкостью до определенного уровня h (рисунок 1).
Из закона Паскаля известно, что столб жидкости высотой h оказывает на дно сосуда давление p, равное ρgh:
p=ρgh, (1)
где ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости.
Высота столба жидкости h во всех трех сосудах одинакова. Жидкости однородны, а значит, и плотность жидкости ρ во всех трех сосудах одинакова. Величина ускорения свободного падения g также является константой. Исходя из формулы (1), получим, что во всех трех случаях жидкости будут оказывать на дно сосудов одинаковое давление p. На основании сказанного можно сделать вывод, что во всех трёх случаях на дно сосудов будет оказываться одинаковое давление p, равное ρgh.
Поскольку массы жидкости в сосудах разные, то сосуды оказывают различное давление на поверхность, на которой они расположены (рисунок 1). Причём, согласно рисунку 1, p**< p < p*.
Так чем же объяснить тот факт, что на дно всех сосудов оказывается одинаковое давление и при этом сосуды оказывают различное давление на поверхность, на которой они расположены? Для этого рассмотрим подробнее каждый из сосудов.
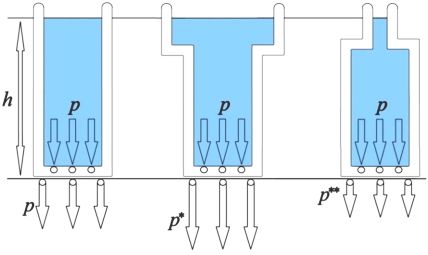
Рис. 1. Сосуды, заполненные жидкостью, оказывающие различные давления на поверхность, на которой они расположены
Рассмотрим первый сосуд (рисунок 2а).
Сосуд заполнен жидкостью до уровня h; ранее мы уже выяснили, что столб жидкости оказывает на дно сосуда давление p, равное ρgh. Считая сосуд невесомым, можно сделать вывод, что давление столба жидкости на дно сосуда полностью передается и на поверхность, на которой расположен сосуд. Таким образом, первый сосуд оказывает на горизонтальную поверхность давление p, равное ρgh.
Рассмотрим второй сосуд (рисунок 2б).
Во втором сосуде жидкость также находится на высоте уровня h. Но за счёт сложной формы сосуда мы имеем не один столб жидкости, а три.
Поскольку жидкость идеальная, то слои жидкости, разграниченные пунктирными линиями на рисунке 2б, проскальзывают относительно друг друга. На дно сосуда будет оказывать давление столб жидкости уровня h, и, как уже упоминалось ранее, давление водяного столба жидкости высотой h на дно сосуда будет равно p=ρgh.
В месте расширения стенок сосуда имеется горизонтальная поверхность, на которую оказывается давление двух столбов жидкости. Высота каждого столба равна h1, а следовательно, давление, оказываемое на горизонтальную поверхность, будет равно p1=ρgh1.
Иными словами, помимо давления p на дно сосуда, на сосуд будет воздействовать ещё два столба жидкости с давлением p1. Из этого и следует, что суммарное давление p*, передаваемое сосудом с жидкостью на горизонтальную поверхность, будет больше, чем давление p, оказываемое на дно сосуда:
p*>p (2)
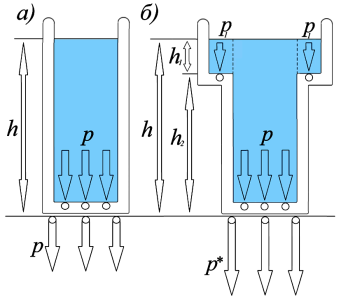
Рис. 2. а - давление жидкости на дно первого сосуда и давление сосуда на поверхность под сосудом; б – давление жидкости на дно и горизонтальные стенки второго сосуда и давление сосуда на поверхность под сосудом
Поясним это неравенство (2). Поскольку S – площадь дна сосуда, а S1 – площадь расширения верхней части сосуда (площадь горлышка сосуда), то площадь горизонтальной верхней стенки будет равна S1-S. Сила F, с которой давление p действует на дно сосуда, равна F=p•S. Сила F1, действующая на горизонтальные верхние стенки, равна F1=p1•( S1-S) и направлена вертикально вниз, как и сила F. Тогда сила, действующая на поверхность, на которой расположен сосуд, равна:
F2=F+F1= p•S+p1•( S1-S)=ρghS+ρgh1•( S1-S)=ρgV+ρgΔV= ρg•(V+ΔV)=ρgV1 , (3)
где V – объем сосуда площадью основания S и высотой h;
ΔV – объем сосуда высотой h1 и площадью основания S1-S;
V1 – объём жидкости в сосуде.
Тогда давление p*, оказываемое сосудом с жидкостью на поверхность, на которой расположен сосуд, равно:
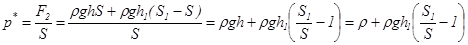 (4)
(4)
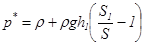 (5)
(5)
Поскольку S1 в выражении (5) изменяется от S до бесконечности, т.е. S1>S, то второе слагаемое в этой формуле больше 0 (положительное). Поэтому давление p* изменяется от p до бесконечности, p*>p.
Переходим к третьему сосуду (рисунок 3).
Сосуд заполнен жидкостью до уровня h. За счёт сложной формы сосуда мы имеем 3 столба жидкости, действующих на дно сосуда: столб жидкости высотой h, и столбы жидкости высотой h2, между которыми нет касательных напряжений, поэтому столбы проскальзывают друг относительно друга. Давление этих столбов жидкости на дно сосуда будет равно p=ρgh для первого столба и p2=ρgh2 для двух других соответственно. Тогда получается, что на разные точки дна сосуда жидкость действует с различным давлением?
Попробуем разобраться, в чём тут дело.
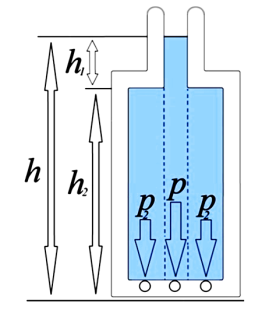
Рис. 3. Давления столбов жидкости высотой h и h2 на дно третьего сосуда
Рассмотрим столб жидкости высотой h1.
Очевидно, что этот столб жидкости будет оказывать давление p1, равное ρgh1, на столб жидкости высоты h2.
Схема, изображенная на рисунке 4а, есть не что иное, как схема опыта для демонстрации закона Паскаля, приведенная в учебниках физики для 7 класса. В качестве шара выступает нижняя часть сосуда высотой h2 с горизонтальными стенками, а в качестве поршня, который оказывает давление p, выступает давление ρgh1 , которое оказывает столб жидкости высотой h1.
Под действием давления столба жидкости высотой h1 верхние слои жидкости на уровне h2 будут оказывать давление на вертикальные и верхнюю горизонтальную стенку сосуда. В этом легко убедиться, если сделать отверстие в верхней горизонтальной стенке. Тогда под давлением жидкость фонтаном начнёт вытекать из сосуда до тех пор, пока уровень жидкости h1 не упадёт до нуля.
На этом этапе объяснения явления мы сталкиваемся с тем, что для полного представления картины обучающимся необходимо знание третьего закона Ньютона, с которым они ещё не знакомы в рамках курса физики 7 класса. Третий закон Ньютона гласит о том, что «Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению». На основании этого можно сделать вывод, что если жидкость действует на верхнюю горизонтальную стенку сосуда, то и сосуд будет действовать на жидкость ровно с таким же давлением, но направленным в противоположную сторону, т.е. вниз.
Из сказанного следует, что на столбы жидкости высотой h2 будет действовать верхняя горизонтальная стенка сосуда с давлением p1=ρgh1 (рисунок 4б).
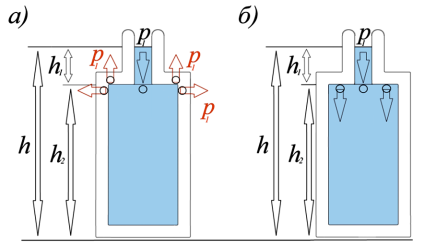
Рис. 4. а – давление жидкости на стенки третьего сосуда; б – давление, оказываемое стенками третьего сосуда на жидкость
Тогда суммарное давление, оказываемое столбом жидкости высотой h2 на дно сосуда, будет складываться из двух составляющих: из давления непосредственно самого столба жидкости высотой h2 на дно сосуда, равного p2=ρgh2, и из давления, оказываемого горизонтальными стенками сосуда на столб жидкости высотой h2, равное p1=ρgh1.
Получим, что суммарное давление, оказываемое столбом жидкости на дно сосуда, равно:
p1+p2= ρgh1+ ρgh2= ρgh=p. (6)
Из этого следует, что на все точки дна сосуда столб жидкости будет оказывать давление, равное p (рисунок 5а).
Рассмотрим теперь давление p**, оказываемое третьим сосудом на поверхность, на которой расположен сосуд. Как было сказано, p**< p. Из этого следует, что сосуд оказывает давление на горизонтальную поверхность, меньшее по величине, чем давление, оказываемое столбом жидкости на дно этого сосуда. Разберемся, почему так происходит.
Ранее уже было отмечено, что жидкость действует на стенки сосуда. В частности, на верхнюю горизонтальную стенку будет оказываться давление p1, равное ρgh1.
Это давление приложено вертикально вверх, и именно оно будет причиной данного парадокса. Это значит, что жидкость будет действовать на дно сосуда с давлением p, но помимо этого, она будет оказывать давление p1 на верхние горизонтальные стенки сосуда, направленное вертикально вверх, то есть как бы приподнимать сосуд.
Сказанным объясняется тот факт, что на поверхность, на которой расположен сосуд с жидкостью, оказывается давление меньшее, чем давление жидкости, оказываемое на дно сосуда, т.е. p**< p (рисунок 5б).
Рассчитаем это давление p**. Поскольку S – площадь дна сосуда, а S1 – площадь зауженной верхней части сосуда (сечения горлышка), то площадь горизонтальной верхней стенки, на которую жидкость действует с давлением p1, будет равна (S – S1).
Сила F1, приподнимающая сосуд, равна F1=p1•(S – S1) и направлена вертикально вверх.
Сила F, с которой давление p действует на дно сосуда, равна F=p•S.
Тогда сила, действующая на поверхность, на которой размещен сосуд, будет равна:
F2=F–F1= p•S – p1•(S – S1)= ρghS – ρgh1(S – S1)=ρgV-ρgΔV= ρg(V-ΔV)= ρgV1,
где: V – объем сосуда площадью основания S и высотой h; ΔV – объём высотой h1 и площадью основания (S – S1); V1 – объём жидкости в сосуде.
Тогда давление p**, оказываемое сосудом с жидкостью на поверхность, на которой расположен сосуд, равно:
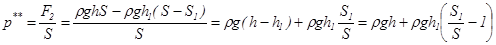 (7)
(7)
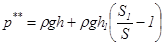 (8)
(8)
Формулы (5) и (8) имеют один и тот же вид.
Поскольку S1 в выражении (8) изменяется от 0 до S, т.е. S1<S, то второе слагаемое в формуле (8) меньше 0 (отрицательное). Поэтому давление p**<p и изменяется от ρgh2 до p.
Действительно, при S1=0 по формуле (8) получаем, что:
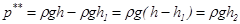 (9)
(9)
Согласно этой формуле, когда исчезает горлышко у сосуда, изображенного на рисунке 5б, то давление, оказываемое на дно сосуда без горлышка с уровнем жидкости h2, равно ρgh2. В этом случае давление, оказываемое невесомым сосудом с жидкостью на поверхность, также равно ρgh2.
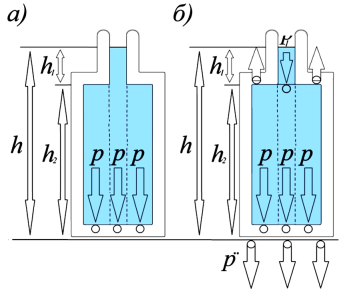
Рис. 5. а – давление жидкости на дно сосуда; б – давления жидкостью на дно и горизонтальные стенки сосуда и давление сосуда с жидкостью на поверхность под сосудом
Построим график зависимости давления p сосудов с жидкостью на поверхность, на которой стоит сосуд, от площади сечения горлышка сосуда S1 (рисунок 6).
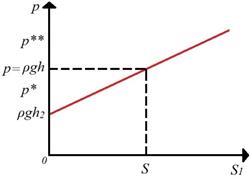
Рис. 6. Зависимость давления сосудов с жидкостью, налитой до уровня h, на поверхность, на которой они расположены, от площади сечения горлышка сосуда S1
Проведенные рассуждения показывают, что полное представление физической картины такого явления, как гидростатический парадокс, невозможно без знания третьего закона Ньютона. Поэтому некорректно рассматривать это явление только в курсе физики 7 класса. В 7 классе, на наш взгляд, в разделе «Гидростатика» нужно лишь упоминать об этом явлении, а вернуться к подробному рассмотрению гидростатического парадокса рационально уже в курсе физики 9 класса, после того как обучающиеся познакомятся с третьим законом Ньютона.
Также нужно отметить методическую целесообразность изображения стенок, расширяющих и зауживающих верхнюю часть сосуда, горизонтальными (как это иллюстрировалось на рисунках в ходе рассуждения), а не под некоторым углом, как это изображается в школьных учебниках (рисунок 7). Это аргументировано тем, что в школьных учебниках давление определяется как «отношение силы, действующей перпендикулярно поверхности, к площади этой поверхности».
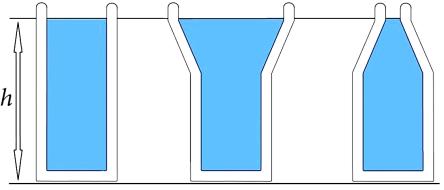
Рис. 7. Методически некорректное изображение сосудов с жидкостью, обычно используемое для объяснения явления гидростатического парадокса
Библиографическая ссылка
Жорник А.И., Кихтенко С.Н., Полеха В.В., Сушкин К.Ю. ГИДРОСТАТИЧЕСКИЙ ПАРАДОКС И ИЗУЧЕНИЕ ЕГО В КУРСЕ ФИЗИКИ СРЕДНЕЙ ШКОЛЫ // Современные проблемы науки и образования. 2019. № 3. ;URL: https://science-education.ru/ru/article/view?id=28879 (дата обращения: 01.07.2025).



