Многие авторы, исследуя процесс создания учебного курса, предлагают представлять содержание учебного материала в виде технологических карт и схем различного типа. Однако необходимым условием внедрения информационно-компьютерных технологий как в обучение, так и в проектирование учебного курса является адаптация образовательного контента к информационной среде и, в частности, его четкая структурированность. Таким образом, создание модели содержания учебного курса является необходимым этапом его проектирования. В этом направлении предлагаются различные подходы, зависящие от цели моделирования. Такой целью может быть создание структуры учебного материала, устанавливающей отношения и связи между его частями, а также отображение построенной структуры в виде схем и таблиц для использования в качестве пособия в учебном процессе. «Ибо усвоить определенную порцию учебных знаний – значит установить их место в структуре данного раздела учебного материала» [1].
Теория моделирования учебного процесса активно развивается разными авторами. В работах [2-4] в рамках формально-алгебраического подхода вводится и исследуется само понятие «модель». В работах [5, 6] подробно разрабатывается технология создания различных карт курса с точки зрения формирования различных компетенций учащихся. Изучению внутрипредметных связей посвящены, например, исследования [7, 8]. А в последнее время активно изучаются способы структурирования учебного материала с целью адаптации к использованию в электронных обучающих ресурсах [9, 10]. При этом ядро любой модели образует структура образовательного контента.
Несмотря на различие предложенных в научной литературе подходов к структурированию учебных курсов и детальную проработку некоторых из моделей, изучение связей между частями структур учебного контента остается недостаточным. В то же время задача классификации типов связей (и, соответственно, типов структур) и задача создания достаточно подробной карты курса с заданным типом связей являются актуальными. Подобные карты и схемы необходимы и преподавателю, создающему учебный курс, и разработчику электронных образовательных ресурсов, который отслеживает различного типа связи между частями контента. Безусловно, полезны подобные разработки и современному студенту, который с их помощью самостоятельно может не только освоить учебный материал, но и выстроить свою образовательную траекторию.
В настоящей статье рассмотрены некоторые аспекты структурирования содержания учебного курса. Особое внимание в работе уделяется изучению логических связей между элементами курса.
Материал и методы исследования
В научной литературе предлагаются различные подходы к созданию структуры учебного курса. Следуя разработанной Ю.Б. Мельниковым теории моделирования, можно представить содержание математического курса как систему моделей (определение модели здесь не совпадает с формально логическим, предложенным ниже): учебный курс как система разделов, как система математических феноменов, как система типов связей между математическими феноменами (обобщение, конкретизация, основа для аналогии и др.), как система методов математической деятельности, как система методов и форм представления материала [4]. При этом способы разработки указанных систем требуют отдельного изучения, включая введение соответствующего понятийного аппарата.
Развивая предложенный в [3, 4] алгебраический подход, а также анализируя другие научные источники, представляется естественным ввести понятие структуры курса и понятие терма. Определим структуру содержания учебного курса как совокупность двух множеств: множества термов и множества связей между термами, распределенных по типам. Термами в свою очередь называются теоретические единицы, представляющие собой семантически законченные порции учебного материала [9]. При классификации по типам связей возникают и различные типы структур. На языке введенных понятий можно обобщить различные с точки зрения степени проработки связей между термами подходы к структурированию учебного курса, выделив два крайних случая.
- Классический «тематический» подход. Проектирование любого учебного курса начинается с выбора тем и последовательности их изучения. По сути результатом такого структурирования является линейное перечисление (последовательность) названий тем и разделов. Соответственно элементами такой структуры (термами) являются разделы курса. Поскольку для изучения некоторого раздела необходимо, как правило, изучить предыдущие, то связи между термами носят общий логико-гносеологический характер. Более того, любые два терма связаны гносеологически просто потому, что это части изучения большого целого (учебного курса). Необходимость этого этапа построения модели курса очевидна, но тогда схема курса выглядит как содержание пособия. Подача материала в этом случае мало отличается от книжного чтения. Недостаток такого подхода – слабая проработка внутрипредметных связей.
- «Программистский» подход, характерный для проектирования электронных образовательных ресурсов. В качестве термов структуры курса могут выступать темы, разделы, понятия. Выстраивается структура в виде графов (деревьев). Связь между термами (вершинами графа) устанавливается разработчиком, если он, например, считает целесообразным подключить тему № 1 к изучению темы № 2. Также с помощью программы можно установить связи по самым разным признакам: число общих слов в двух термах, степень сложности тем, трудоемкость вычислений и т. п. Благодаря компьютерной обработке устанавливается большое число связей, обладающих разными свойствами. Если нужно выделить связи строго логические, придется предусмотреть это отдельной программой. Однако создание логической подструктуры пока требует участия разработчика курса. Такой (компьютерный) подход может вобрать все возможные типы связей и имеет большой потенциал.
Как видно из приведенных примеров, типы связей между термами могут быть самыми разными. Однако наиболее важными в контексте создания математического курса являются связи «логического типа». Отнесем к ним следующие: «если А, то В» ( «А частный случай В», «В обобщение А», «А модель теории В»), «А эквивалентно В», «А и С модели одной теории В», «изучение раздела В является необходимым условием для изучения раздела А». В частности, выбор последовательности изучения термов – от частного к общему или наоборот – подразумевает использование связей логического типа.
Результаты исследования и их обсуждение
Для математического курса при создании логических структур разного уровня отслеживание логических связей в форме «теория – модель» представляется наиболее информативным. В данном случае понятия «теория» и «модель» используются в следующем смысле: «если модель, то теория». В формально логическом смысле теория Т по определению – некоторое множество формул языка в рамках данного исчисления; модель М теории Т – такая интерпретация формальных конструкций языка (слов, символов и т. п.), при которой все формулы из Т являются истинными высказываниями. Это определение также работает в связях указанного типа. В более общепринятом смысле теория есть обобщение модели. Например, алгебра множеств (модель) есть булева алгебра (теория), но и алгебра высказываний есть модель булевой алгебры. В силу богатства и сложности логической структуры математического курса естественно выделять наиболее значимые связи между термами, а в качестве термов рассматривать объекты разного уровня. Таким способом формируются различные «срезы» образовательного контента.
Обобщая приведенные соображения, можно предложить следующие этапы создания логической структуры содержания учебного курса.
- Создание «тематической» структуры – линейной структуры тем и разделов, соединенных логико-гносеологическими связями (или связями типа «часть – целое»).
- Создание структуры первого уровня – структуры тем, соединенных логико-гносеологическими связями.
- Создание структуры второго уровня – структуры темы. В качестве термов выступают разделы темы, соединяются термы логическими связями, например типа «теория – модель».
- Создание структуры третьего уровня – структура раздела темы. В качестве термов могут выступать теоремы, понятия и иное, соединяются термы логическими связями.
Для нелинейных структур второго и больших уровней возможно изображение в виде графа. Заметим, что если целью создания логической структуры является повышение качества обучения, наглядное представление логических связей, отслеживание различных траекторий обучения, то нет необходимости в повышении уровня структур.
Приведенные соображения использовались при создании логической структуры курса «Дискретная математика», читаемого в физико-технологическом институте и в институте радиотехнических и информационных технологий Уральского федерального университета для специальностей направления «Прикладная математика» и направления «Математическое обеспечение и администрирование информационных систем». Эту структуру, кроме тематической подструктуры, составили пять логических карт, оформленных в виде графов. В качестве контроля проработки логических связей типа «теория – модель» студентам были предложены три контрольные работы. Далее приведены примеры некоторых элементов созданной структуры.
На первом этапе, создавая «тематическую» структуру, весь материал, соответствующий требованиям ФГОС, распределяем по темам и разделам. Например: тема «Общая алгебра», раздел «Универсальные алгебры», подраздел: 1.1 «Алгебраические операции, определение алгебры» и т.д. Фактически это содержание учебного пособия автора по данному курсу [11].
Структура первого уровня, структура тем изображена на рисунке 1 в виде графа, вершины которого есть темы, условно распределенные на теоретические и приложения. Ребра графа соответствуют общим логико-гносеологическим связям.
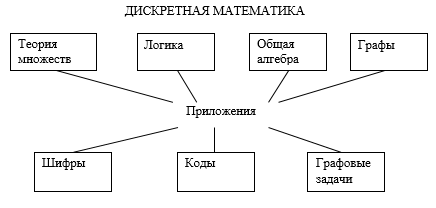
Рис. 1. Пример структуры первого уровня
Более сложной и более информативной является структура второго уровня, которая для темы «Общая алгебра» изображена на рисунке 2. Разделы этой темы размещены в прямоугольных блоках, разделы из других тем размещены в овалах. Ребра графа в виде стрелки изображают связь модель теория. Неориентированные ребра играют дополнительную роль и выделяют разделы темы, необходимые для изучения приложений. АБФ обозначает здесь алгебру булевых функций, АВ – алгебра высказываний, АМ – алгебра множеств, P[x] – кольцо многочленов над полем P, Z – кольцо целых чисел.
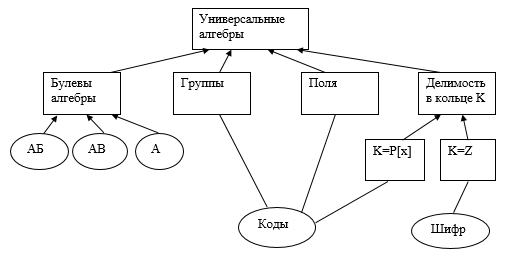
Рис. 2. Пример структуры второго уровня
Использовать такую диаграмму можно для наглядной демонстрации учащимся логических связей между математическими понятиями. Кроме того, при выборе последовательности изложения учебного материала от частного к общему, например, преподаватель будет рассматривать в первую очередь модели, двигаясь к обобщению – теории. Возможно и противоположное движение – от общего к частному. Далее, если целью является изучение шифрования с открытым ключом, например, то достаточно рассмотреть лишь модель «делимость в кольце целых чисел», в то время как изучение темы «коды» вбирает в себя три раздела и является намного более трудоемким. Таким образом, наглядно видны возможности для различных образовательных траекторий. В случае создания структуры третьего уровня потребуется устанавливать логические связи между понятиями и теоремами, что требует довольно детальной проработки в силу богатства набора таких связей. Однако с методической точки зрения проработка связей в структуре второго уровня представляется более важной.
В рамках деятельностного подхода к формированию таких требуемых ФГОС компетенций, как умение на основе анализа увидеть и корректно сформулировать математически точный результат (ПК 5), умение самостоятельно увидеть следствия сформулированного результата (ПК 6), студентам предлагалось, основываясь на логических картах, самостоятельно провести аналогии между моделями одной теории. На рисунке 3 представлен фрагмент шаблона для контрольной работы. Слева дан набор понятий теории делимости целых чисел, справа требуется сформулировать соответствующее понятие теории делимости многочленов.
|
Делимость в Z |
Делимость в P[x] |
|
Простое число |
|
|
Каноническое разложение на простые множители |
|
|
Сравнимость целых чисел по модулю n |
|
Рис. 3. Примеры задач на установление аналогий между моделями одной теории
Способность к обобщению и к построению правильных умозаключений через изучение логических связей и поиск аналогий формирует у студентов компетенции «высокого» уровня. В конечном счете предложенный опыт создания логических структур работает на формирование «математической культуры как инфраструктуры для обработки информации» [4].
Заключение
В современных условиях бурного развития информационно-компьютерных технологий актуален вопрос качества содержания математических курсов. Сейчас нет необходимости уделять много времени вычислительным алгоритмам и задачам, требующим рутинного счета. Таким образом, можно реализовать возможность повышения качества математического содержания курсов, в первую очередь отслеживая логическое строение математических теорий и понятий. Этот подход должен реализовываться в проектировании учебного математического курса. Предложенный в работе способ проработки логических связей между частями учебного курса является одним из вариантов структурирования образовательного контента. Полученные структуры, представленные в виде диаграмм, использовались автором в педагогической практике. Результатом использования стало более качественное усвоение материала студентами, более ясное понимание архитектуры математики в целом. Логические карты использовались как часть образовательного контента наряду с технологическими картами и разнообразными электронными ресурсами. Однако в связи с развитием информационно-компьютерных технологий представляется реальной задача программной реализации процесса установления логических связей между термами. В этом контексте развитие формально-алгебраического подхода к проектированию учебных курсов является вполне перспективным.
Библиографическая ссылка
Голикова Е.А. ОПЫТ ПОСТРОЕНИЯ СТРУКТУРЫ КУРСА «ДИСКРЕТНАЯ МАТЕМАТИКА» С ОТСЛЕЖИВАНИЕМ ЛОГИЧЕСКИХ СВЯЗЕЙ МЕЖДУ ЕЕ КОМПОНЕНТАМИ // Современные проблемы науки и образования. – 2018. – № 5. ;URL: https://science-education.ru/ru/article/view?id=28165 (дата обращения: 26.04.2024).



