В связи с переходом к двухуровневой системе образования (бакалавр - магистр) возникает много новых вопросов, связанных с организацией самостоятельной работы студента, с выбором необходимого учебного материала.
В последнее время все активнее обсуждается возможность введения элементов дистанционного обучения в систему высшего образования. Зарубежные авторы в настоящее время активно обсуждают достоинства и недостатки дистанционного образования [1-3], указывают на различие между понятиями «дистанционное обучение» и «электронное образование» (e-learning), обсуждают использование компьютерных сетей в образовании. В российском высшем образовании в настоящее время системы электронного и дистанционного образования до сих пор воспринимаются как новые, малоизученные и нетрадиционные формы организации образовательного процесса, поэтому российские авторы часто основное внимание уделяют описанию конкретных образовательных электронных ресурсов [4-6]. В настоящее время вряд ли можно однозначно положительно ответить на вопрос, является ли дистанционное обучение более эффективным, чем традиционные контактные формы. Здесь все зависит от конкретной дисциплины и конкретной образовательной ситуации. Скажем, отсутствие достаточно квалифицированного специалиста по данной дисциплине в конкретном вузе может сделать целесообразным дистанционное обучение, проводимое специалистом, приглашенным из другого вуза (причем, возможно, весьма удаленного от аудитории слушателей курса).
Цель исследования. Целью данного исследования является анализ применения дистанционного курса при изучении дисциплины «Элементы теории специальных функций».
Методы исследования. Для разработки и обоснования полученных в статье результатов использовался метод сопоставительного анализа, а также метод экспериментального подтверждения теоретических гипотез. В частности, были проанализированы научные и методические источники, посвященные разработке элективных курсов, проанализирована специальная математическая литература, проведена апробация курса в нескольких академических группах студентов. Применялись педагогический эксперимент, анкетирование, тестирование, опрос обучаемых.
Постановка проблемы и предполагаемые пути ее решения. Рассмотрим некоторые возникающие в связи с применением дистанционного обучения проблемы на примере студентов, обучающихся в Елабужском институте Казанского федерального университета по четырехлетней программе бакалавриата направления 02.03.01 - математика и компьютерные науки, профиль специализации - математическое и компьютерное моделирование.
На четвертом курсе студенты изучают в первом семестре традиционный курс «Уравнения математической физики», на который отводится 46 часов лекций и 44 часа практики. Конечно же, такого количества аудиторных занятий совершенно недостаточно для глубокого изучения такого курса, поэтому многие, давно ставшие классическими, разделы вынужденно должны «ужаться» лишь до некоторого упоминания о соответствующих понятиях (например, теория обобщенных функций, теория специальных функций, теория потенциала).
Во втором семестре те же студенты изучают «Математическое моделирование» - курс, который непосредственно перекликается с уже упомянутым курсом «Уравнения математической физики» и даже может рассматриваться как некоторое его продолжение. Но все же в рамках курса «Математическое моделирование» в первую очередь следует не наверстывать не пройденный ранее теоретический материал, а стремиться исследовать уже имеющимися в багаже студентов средствами как можно больше содержательных математических моделей.
Раздел математики, который можно назвать «Элементы теории специальных функций» традиционно преподается (при наличии достаточного времени) в рамках курса «Уравнения математической физики». С другой стороны, имеется ряд содержательных математических моделей, требующих для решения соответствующих краевых задач применения специальных функций. То есть упомянутые модели могли бы удачно дополнить курс «Математическое моделирование». В результате приходим к целесообразности наличия курса «Элементы теории специальных функций» во втором семестре последнего года обучения бакалавров. Этот курс естественно разместить в вариативной части блока Б3 (Б3.ДВ).
Приходим к следующей ситуации: свойства специальных функций (в предлагаемом курсе это цилиндрические функции) изучаются хорошо знакомыми студентам методами математического анализа, а краевые задачи, для решения которых используются цилиндрические функции, решаются в основном уже хорошо изученным в рамках курса «Уравнения математической физики» методом разделения переменных. Это означает, что у студентов не возникает принципиальных трудностей с освоением теоретического материала и с решением предложенных задач.
В связи с этим возникла идея разгрузить напряженный второй семестр выпускного четвертого курса, переведя изучение «Элементов теории специальных функций» на дистанционную форму, реализуемую электронным образовательным ресурсом, что, конечно, значительно экономит время студентов на изучение дисциплины, при этом не снижая уровня усвоения материала.
Отметим, что на курс «Элементы теории специальных функций» отводится 18 часов лекций, 18 часов семинарских занятий, самостоятельная работа составляет 36 часов, завершается курс экзаменом. Такое количество отводимого для курса времени, на наш взгляд, позволяет достаточно фундаментально изучить необходимый учебный материал. Изучение специальных функций является неотъемлемой частью подготовки будущих математиков. Для эффективного изучения дисциплины необходима организация процесса самостоятельной работы. Эту задачу также можно решить с помощью дистанционного электронного образовательного ресурса.
Содержание электронного образовательного ресурса. Данный курс создавался на базе системы LMS MOODLE.
Мы не будем подробно останавливаться на структуре электронного образовательного ресурса, поскольку она стандартна и принципиально не отличается от описанной в [7]. В нашем конкретном случае обоснование целесообразности такого ресурса обсуждалось выше.
Приведем список разделов, составляющих содержание дистанционного курса «Элементы теории специальных функций». Подробно опишем содержание теоретического материала, который надлежит изучить студентам.
Тема 1. Уравнение Бесселя.
Данная тема включает в себя следующий материал: основные сведения о гамма-функции и бета-функции, в том числе интегральное представление гамма-функции, ее связь с понятием факториала, интегральное представление бета-функции, ее связь с гамма-функцией, приложения бета-функции к вычислению интегралов, в том числе от тригонометрических функций; уравнение специальных функций и свойства его решений, уравнение Бесселя, степенной ряд для функций Бесселя, рекуррентные формулы для функций Бесселя, связывающие функции различных порядков и их производные, функции Бесселя полуцелого порядка и их связь с тригонометрическими функциями.
Тема 2. Интегральные представления цилиндрических функций.
Основное содержание раздела составляет определение функций Ханкеля, Неймана, Инфельда и Макдональда посредством интегральных представлений, а также изучение свойств указанных функций (в частности, их асимптотики). Рассмотрены интегральное представление функций Бесселя, интегральное представление функций Ханкеля, рекуррентные соотношения для функций Ханкеля, формулы, выражающие функции Бесселя через функции Ханкеля, определение функций Неймана через функции Ханкеля, формулы, выражающие функции Ханкеля через функции Бесселя и Неймана. Здесь же доказывается линейная независимость цилиндрических функций, указано асимптотическое поведение указанных функций при стремлении аргумента к нулю и к бесконечности. Рассмотрены цилиндрические функции мнимого аргумента (функции Инфельда и Макдональда), указаны их свойства.
Тема 3. Ряд Фурье-Бесселя.
Здесь рассмотрены ортогональность цилиндрических функций, построение решений краевых задач в виде рядов Фурье-Бесселя.
Отметим, что весь теоретический материал непосредственно опирается на изученные студентами ранее математические теории или является логическим продолжением изученных ранее разделов математики. Поэтому студенты в состоянии самостоятельно разобрать весь теоретический материал предложенного спецкурса, не встречая принципиальных затруднений.
Помимо теоретического материала, каждая тема содержит практические задания для самостоятельной работы (задачи для самостоятельного решения). Каждое практическое занятие содержит примеры решений основных классов задач, относящихся к пройденному лекционному материалу, включает в себя несколько задач и предлагаемые студенту действия для самостоятельного решения задач.
Приведем примеры задач, рассматриваемых в рамках каждой темы.
Задачи, относящиеся к теме 1.
1. Гамма-функция определяется равенством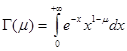 
. Доказать, что 
, 
.
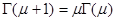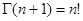2. Доказать, что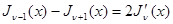 
.
3. Показать, что корни уравнения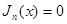 
, 
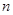– натуральное число, могут быть только действительными и, кроме того, уравнения 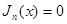и 
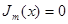с различными натуральными индексами не могут иметь общих корней, отличных от нуля.
Задачи к теме 2.
1. Вычислить интеграл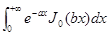 
.
2. Вычислить интеграл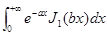 
.
3. Вычислить интеграл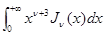 
.
Задачи по теме 3.
1. Найти потенциал электростатического поля внутри цилиндрической коробки круглого сечения, оба основания которой заземлены, а боковая поверхность заряжена до потенциала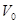 
. Определить напряженность поля на оси.
2. Цилиндр, радиус основания которого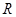 
и высота 
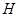, имеет температуру нижнего основания и боковой поверхности, равную нулю, а температура верхнего основания есть заданная функция 
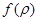). Найти стационарную температуру внутренних точек цилиндра.
3. Найти стационарное распределение концентрации неустойчивого газа внутри бесконечного цилиндра кругового сечения, если на поверхности цилиндра поддерживается постоянная концентрация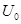 
.
В качестве основных источников информации, послуживших основой для создания курса, укажем книги [8-9].
В состав дистанционного курса входит также итоговое тестирование, которое позволяет студенту и преподавателю оценить степень понимания теоретического материала и готовность студента к экзамену по дисциплине. Итоговое тестирование является заключительным для студента этапом прохождения курса «Элементы теории специальных функций». По прохождении итогового тестирования студент переходит на страницу с результатами теста. Так как студенты сдают экзамен (в классической форме), тестовые задания предназначены прежде всего для самоконтроля. Студенты, пройдя тестовые задания, определяют, насколько внимательно они прочитали лекционный материал, насколько глубоко усвоили каждую тему. Обнаружив у себя неправильные ответы, они могут заново изучить проблемные темы и пройти тестирование повторно.
Приведем примеры тестовых заданий.
1. Какая из формул справедлива:
а)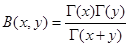 
, б) 
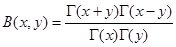, в)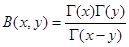 
.
2. Какая из формул имеет место:
а)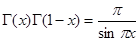 
, б) 
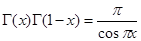, в)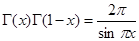 
.
3. Функция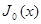 
удовлетворяет уравнению:
а)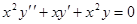 
, б) 
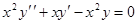, в)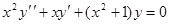 
.
4. Какое из соотношений справедливо:
а)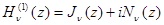 
, б) 
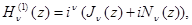в)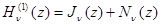 
.
5. Выберите верное равенство:
а)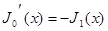 
, б) 
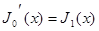, в)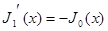 
.
6. Функция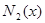 
в точке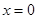 
а) имеет полюс, б) имеет логарифмическую особенность, в) не имеет особенности.
Выводы. Данный электронный образовательный ресурс «Элементы теории специальных функций» позволяет внедрить дистанционные образовательные технологии в обучение студентов направления «Математика и компьютерные науки». Внедрение ЭОР оправданно, поскольку снижает аудиторную нагрузку на студентов, позволяет им в параллельном режиме решать задачи, непосредственно связанные с двумя смежными курсами: «Уравнения математической физики», «Математическое моделирование», дополняет материал этих курсов содержательными прикладными задачами. Как правило, эффективность ЭОР при изучении какого-либо раздела математики объясняется тем, что студенты затрачивают гораздо больше времени (и сил) для изучения такого курса по сравнению с традиционной методикой преподавания. Студенты поставлены в очень жесткие условия, они в заранее отведенные сроки изучают теорию, затем решают большое количество задач, проходят тестирование. В случае неудачи на этапе защиты домашнего задания или тестирования они вынуждены повторно изучить новый для себя материал, снова пройти контроль и т.д. Это во многих случаях приводит к эмоциональной и интеллектуальной перегрузке. Грубо говоря, затратив в два раза больше времени, студенты показывают знание материала на 10% лучше, чем в контрольной группе, обучающейся традиционно. В нашем случае речь идет не об изучении принципиально новых математических теорий, а о расширении круга решаемых задач с помощью уже изученных математических теорий и методов. На наш взгляд, данный ЭОР приводит не к дополнительной нагрузке на студента, а к разгрузке, при этом достигается тот же результат, что и при аудиторной форме проведения занятий.
Библиографическая ссылка
Гильманова Г.Р., Миронов А.Н., Миронова Л.Б. О МЕСТЕ КУРСА ПО ВЫБОРУ «ЭЛЕМЕНТЫ ТЕОРИИ СПЕЦИАЛЬНЫХ ФУНКЦИЙ» В СИСТЕМЕ ОБУЧЕНИЯ БАКАЛАВРОВ НАПРАВЛЕНИЯ «МАТЕМАТИКА И КОМПЬЮТЕРНЫЕ НАУКИ» // Современные проблемы науки и образования. – 2017. – № 6. ;URL: https://science-education.ru/ru/article/view?id=27259 (дата обращения: 20.04.2024).