Механическая стрижка овец – заключительный этап получения основного продукта шерстного овцеводства – шерсти. Качество получаемой продукции во многом зависит не только от породы животных, но и от организации и осуществления технологического процесса.
Целью наших исследований является выявление и оценка проблемных участков технологического процесса, а также определение перспективных направлений по совершенствованию механической стрижки овец. Для достижения поставленной цели мы использовали математическое моделирование. Под математической моделью в технике понимают адекватную замену исследуемого технического устройства или процесса соответствующей математической моделью и ее последующим изучением с применением средств современной вычислительной техники [3]. Таким образом, в наших исследованиях под математическим моделированием мы подразумеваем установленное соответствие реальному объекту (процесс механической стрижки овец), некоторого математического объекта, называемого математической моделью, исследуя которую можно получить характеристики рассматриваемого реального объекта.
В наших исследованиях [9, 10] доказано, что процесс механической стрижки овец следует рассматривать как сложную биотехническую систему (БТС).
Методов математического описания сложных систем существует достаточно много [3, 6, 7]. Наиболее близким к рассматриваемому процессу являются методы, базирующиеся на вероятностно-статистическом принципе, они позволяют получить обобщенные и адекватные математические модели функционирования на множестве производственных условий.
Для разработки математической модели нами выбраны марковские процессы с дискретным состоянием и непрерывным временем. Базируясь на этом, принимаем, что переходы системы из одного состояния в другое происходит не в фиксированные, а случайные моменты времени, которые заранее предсказать весьма проблематично. К примеру, стресс биологического объекта БТС может произойти в любой момент времени, и выход из этого состояния может произойти в неопределенный момент времени. Схема случайных марковских процессов с достаточной точностью описывает такие процессы при принятии ограничительных допущений, которые не противоречат статистическим и экспериментальным данным:
- число состояний конечно;
- для каждого момента времени ![]() , вероятность любого состояния системы в последующем (при
, вероятность любого состояния системы в последующем (при ![]() ) зависит только от состояния системы в настоящем (
) зависит только от состояния системы в настоящем (![]() ) и не зависит от того, когда и каким образом система оказалась в этом состоянии [10].
) и не зависит от того, когда и каким образом система оказалась в этом состоянии [10].
Для более информативного и детального рассмотрения динамики изменений состояний БТС нами строился размеченный граф состояний (графовая математическая модель), представленный на рис. Вершинам графа соответствует состояния Sо1, Sу1, Sж1. Принимаем, что это состояние системы является исходным или желательным. Каждому из этих состояний соответствует вероятность пребывания системы в этом состоянии Р(Sо1), Р(Sу1), Р(Sж1).
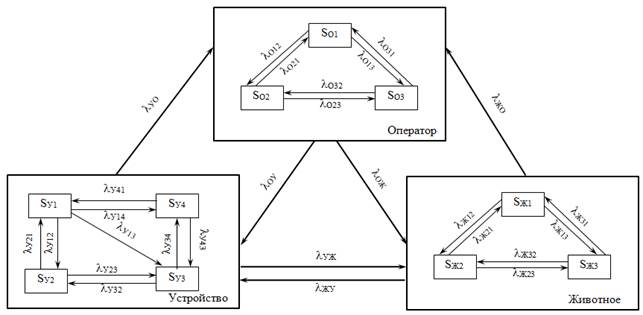
Рис. Графовая математическая модель состояния биотехнической системы процесса стрижки овец
Обозначения соответствуют следующим состоянием каждой из подсистем.
Подсистема «Оператор»
So1 – оператор выполняет процесс механической стрижки шерстного покрова животного в соответствии с технологическим регламентом и способствует получению продукции высокого качества; So2 – оператор не полностью выполняет технологический регламент, что не способствует получению продукции высокого качества; So3 – оператор выполняет технологический регламент с грубыми нарушениями, что приводит к получению продукции низкого качества, нарушению работы подсистемы «устройство», ухудшению физиологического состояния подсистемы «животное».
Подсистема «Устройство»:
Sу1 – устройство в рабочем состоянии, способствует получению продукции высокого качества; Sу2 – устройство в рабочем состоянии, но требует регулировки конструктивно- режимных параметров, получаемая продукция высокого или среднего качества; Sу3 – устройство допускает отказы в работе и снижает качество получаемой продукции; Sу4 – устройство не работоспособно.
Подсистема «Животное»:
Sж1 – животное в нормальном физиологическом состоянии, получаемая продукция – высокого качества; Sж2 – животное в беспокойном состоянии, но получаемая при этом продукция удовлетворительного качества; Sж3 – животное в беспокойном состоянии, наблюдается снижение продуктивности и качество получаемой продукции.
Виды состояния подсистем и переходы между ними определены на основании исследований БТС Л.П. Карташова, Л.В. Погорелова, М.М. Луценко, А.А. Алексеенко [1, 3, 6].
Используя уравнения Колмогорова для вероятностей состояний [2, 8], мы получили систему дифференциальных уравнений (1), которую и принимаем за математическую модель технологического процесса стрижки овец.
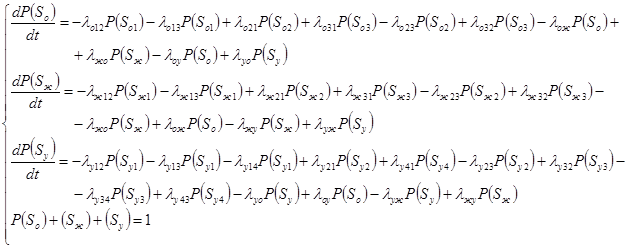 (1)
(1)
где ![]() – интенсивность перехода подсистемы из состояния Si в состояние Sj .
– интенсивность перехода подсистемы из состояния Si в состояние Sj .
Для решения этих уравнений необходимо задать начальные условия. Приняв условие, что в начальный момент времени вся система находится в состоянии S1, тогда все остальные вероятности будут равны 0.
В теории случайных процессов [2, 8] доказывается, что если число n состояний конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое, то существуют финальные вероятности. При t®¥ в системе устанавливается предельный стационарный режим, при котором система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. А если вероятности постоянные, то их производные равны нулю. Таким образом, для нахождения финальных вероятностей необходимо все левые части уравнений системы дифференциальных уравнений положить равными нулю, в результате получается система линейных алгебраических уравнений.
Исходя из вышеизложенного, имеем для подсистем «Оператор»:
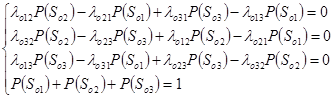 (2)
(2)
для подсистемы «Устройство»:
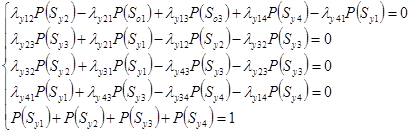 (3)
(3)
для подсистемы «Животное»:
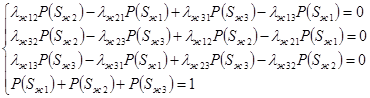 (4)
(4)
Проведя замены и упрощения в системах (2, 3, 4) и задавшись интенсивностями перехода подсистем из одного состояния в другое можно определить вероятности нахождения каждого звена биотехнической системы в том или ином состоянии, а так же оценить надежность функционирования каждой подсистемы.
Величины интенсивности перехода ![]() зависят от ряда условий – квалификации и подготовленности оператора, степени износа и функциональной надежности устройства (стригальной машинки), стрессоустойчивости животного. В нижеприведенных таблицах 1, 2, 3 представлены значения
зависят от ряда условий – квалификации и подготовленности оператора, степени износа и функциональной надежности устройства (стригальной машинки), стрессоустойчивости животного. В нижеприведенных таблицах 1, 2, 3 представлены значения![]() для каждого звена БТС.
для каждого звена БТС.
Величины ![]() для звена «Оператор» определены на основании хронометража рабочего времени стригалей средней квалификации (сменная выработка 30–35 голов) данных, полученных другими исследователями.
для звена «Оператор» определены на основании хронометража рабочего времени стригалей средней квалификации (сменная выработка 30–35 голов) данных, полученных другими исследователями.
Таблица 1
Интенсивность перехода звена БТС «Оператор»
|
lо |
|
|
|
|
|
|
|
Знач., (ч) |
1/2 |
1/6 |
1 |
5/12 |
1/6 |
1/4 |
Для определения интенсивности перехода ![]() звена «Устройство» (стригальная машинка) взяты данные полученные Алексеенко Н.П. и Малашенко Н.П. [1, 4], а также материалы собственных исследований.
звена «Устройство» (стригальная машинка) взяты данные полученные Алексеенко Н.П. и Малашенко Н.П. [1, 4], а также материалы собственных исследований.
Таблица 2
Интенсивность перехода звена БТС «Устройство»
|
lу |
|
|
|
|
|
|
|
|
|
|
Знач., (ч) |
1 |
2 |
2,5 |
0,25 |
0,5 |
1 |
1/3 |
5 |
1,5 |
Интенсивность перехода ![]() звена «Животное» определена по результатам собственных наблюдений, исследований В.Д Позднякова, Ю.А. Мирзоянца [5, 7] и исследований «Этология сельскохозяйственных животных» под общей редакцией Панова Е.Н.
звена «Животное» определена по результатам собственных наблюдений, исследований В.Д Позднякова, Ю.А. Мирзоянца [5, 7] и исследований «Этология сельскохозяйственных животных» под общей редакцией Панова Е.Н.
Таблица 3
Интенсивность перехода звена БТС «Животное»
|
lж |
|
|
|
|
|
|
|
Знач., (ч) |
1/6 |
1/4 |
1/4 |
2/3 |
1/12 |
1/2 |
Таким образом, используя интенсивности перехода в каждом из звеньев БТС, нами получены вероятности пребывания подсистем в каждом из возможных состояний, на наш взгляд, полученные результаты можно интерпретировать как оценки функционирования каждого звена в отдельности и всей системы в целом.
Для подсистемы «Оператор» получены следующие вероятности:![]() ,
, ![]() =34 %. Эти результаты можно истолковать следующим образом – оператор (стригаль) с вероятностью 55 % будет находиться в благоприятном для функционирования БТС состоянии So1 и осуществлять процесс механической стрижки овец в соответствии с технологическим регламентом и способствовать получению продукции высокого качества. Для повышения вероятности нахождения стригаля в этом состоянии необходимо повышать его квалификацию, соблюдать режим труда и отдыха, оптимизировать по времени технологический процесс.
=34 %. Эти результаты можно истолковать следующим образом – оператор (стригаль) с вероятностью 55 % будет находиться в благоприятном для функционирования БТС состоянии So1 и осуществлять процесс механической стрижки овец в соответствии с технологическим регламентом и способствовать получению продукции высокого качества. Для повышения вероятности нахождения стригаля в этом состоянии необходимо повышать его квалификацию, соблюдать режим труда и отдыха, оптимизировать по времени технологический процесс.
В результате решения системы 3, получили вероятности нахождения устройства (стригальная машинка МСУ-200, третий сезон эксплуатации) в том или ином состоянии: ![]() ,
, ![]() ,
, ![]() =7%
=7%![]() . Анализируя эти вероятности, мы пришли к выводу, что необходимо вести целенаправленную работу на совершенствование конструкции устройства, его отдельных узлов, использовать при конструировании более износостойкие материалы (особенно актуально для элементов режущей пары).
. Анализируя эти вероятности, мы пришли к выводу, что необходимо вести целенаправленную работу на совершенствование конструкции устройства, его отдельных узлов, использовать при конструировании более износостойкие материалы (особенно актуально для элементов режущей пары).
Наименее управляемое звено БТС «Животное» находится в том или ином состоянии с вероятностью ![]() ,
, ![]() ,
, ![]() =64 %. Это свидетельствует, что при увеличении продолжительности технологического процесса стрижки животное начинает испытывать дискомфорт, а, возможно, и болевые ощущения, которые могут негативно сказываться на продуктивности и физиологическом состоянии в будущем. Следовательно, повышение квалификации стригаля, совершенствование стригальной машинки позволит сократить продолжительность обслуживания одного животного, минимизируя при этом негативные последствия.
=64 %. Это свидетельствует, что при увеличении продолжительности технологического процесса стрижки животное начинает испытывать дискомфорт, а, возможно, и болевые ощущения, которые могут негативно сказываться на продуктивности и физиологическом состоянии в будущем. Следовательно, повышение квалификации стригаля, совершенствование стригальной машинки позволит сократить продолжительность обслуживания одного животного, минимизируя при этом негативные последствия.
Рецензенты:
Карташов Л.П., д.т.н., профессор, профессор кафедры механизации технологических процессов в АПК, Оренбургский государственный аграрный университет, г. Оренбург;
Комарова Н.К., д.с-х.н., профессор, заведующий кафедрой физики, Оренбургский государственный аграрный университет, г. Оренбург.
Библиографическая ссылка
Хлопко Ю.А., Осипова А.М. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ФУНКЦИОНИРОВАНИЯ БИОТЕХНИЧЕСКОЙ СИСТЕМЫ ПРОЦЕССА МЕХАНИЧЕСКОЙ СТРИЖКИ ОВЕЦ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=21349 (дата обращения: 17.11.2025).



