В настоящее время только единичные технологические решения, используемые в производстве, соответствуют одному из главных принципов оптимального измельчения – «не дробить ничего лишнего». Переизмельчение материала, обусловленное требованиями технологии по рациональному гранулометрическому составу готового к употреблению продукта, предопределяет рост энергоемкости процесса, а также требует дополнительных энергозатрат на классификацию частиц материала по фракциям. По мере сокращения размеров частиц проявляется фактор их упрочнения, что влечет за собой необходимость более «тонкой настройки» режимов работы электромагнитных механоактиваторов (ЭММА) для реализации соответствующих стадий диспергирования при соблюдении условия минимальных энергозатрат [1,2,3]. В ЭММА с увеличением подведенной мощности при упрочнении частиц происходит аккумулирование некоторой части энергии, что способствует улучшению реакционных качеств материала [4,5,6]. Между тем, согласно физико-механическим основам процессов разрушения материалов, кинетическая энергия, подводимая к перерабатываемому продукту с помощью рабочих органов механоактиваторов, переходит в потенциальную энергию упругих деформаций частиц продукта, которая трансформируется в поверхностную энергию, кинетическую энергию частиц, а также тепловую энергию. Неизбежные тепловые потери наблюдаются в каждой точке энергонапряженного контактного взаимодействия размольного ферромагнитного элемента с продуктом в процессе передачи энергии разрушения. В результате теоретических и экспериментальных исследований электромагнитных механоактиваторов выявлено, что величина разрушающего усилия в магнитоожиженном слое ферротел, при прочих равных условиях, зависит от теплового режима работы аппарата [7,8]. Следовательно, энергоэффективность процесса и качество готовой продукции в значительной степени определяется распределением температурного поля в рабочих объемах ЭММА [9,10].
Целью исследования является разработка метода теплового расчета ЭММА, предназначенного для системного комплексного поиска и проектирования новых конструктивных форм ЭММА, отвечающих требованиям производства по энергетическим и качественным показателям выпускаемой продукции.
Материал и методы исследований. Исследовано тепловое поле электромагнитного механоактиватора, представленного двухмерной моделью. Использованы аналитические и экспериментально-статистические методы исследований.
Результаты исследования и их обсуждение. Алгоритм расчета стационарного теплового поля разработан с целью установления заданного технологией теплового режима обработки продуктов (какаовеллы, семян люпина, негашеной извести, шлака, золы и др.) в рабочих объемах ЭММА цилиндрического исполнения [11] при проектировании и обосновании новых конструктивных решений. Проведено преобразование трехмерных моделей ЭММА в двумерные (рисунки 1,2,3). Тепловое поле рассмотрено в стационарном режиме как функция двух переменных. Такой подход к решению задачи позволил значительно упростить и сократить процедуру расчета при поиске новых конструктивных форм энергоэффективных ЭММА. Метод апробирован при проектировании конструктивных форм электромагнитных механоактиваторов [11,12].
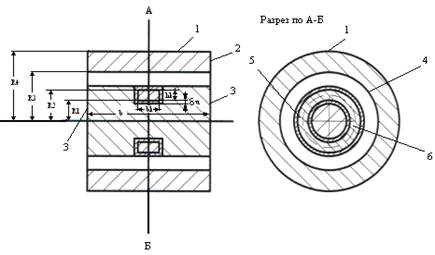
Рис.1. Цилиндрическая модель ЭММА:
1– цилиндрическая поверхность корпуса; 2 – торцевая поверхность корпуса; 3 – торцевая поверхность ротора; 4 – внутренняя поверхность корпуса; 5 и 6 – поверхности, ограничивающие ОУ
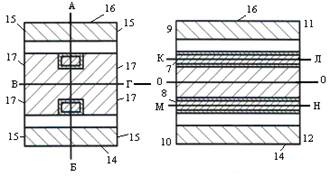
Рис.2. Двумерная модель ЭММА: 11…17 – условные обозначения исследуемых поверхностей
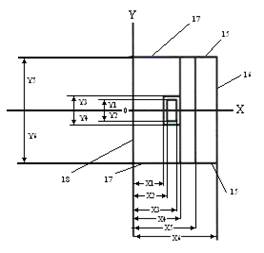
Рис.3. Координаты расчетных точек
Область, ограниченная координатами x2 ≤ x ≤ x3; у2 ≤ у ≤ у1, заполнена обмоткой управления (ОУ), в которой имеется тепловой источник постоянной величины Р = Р0, представляющий тепловые потери, выделяющиеся в единичном объеме обмотки. Коэффициент теплопроводности области c обмоткой представляет некоторый эквивалентный коэффициент теплопроводности λк, обусловленный наличием в этом объеме меди, изоляции проводов и промежутков между ее витками.
Область, ограниченная координатами:
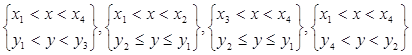 ,
,
заполнена изоляцией ОУ, имеющей постоянный коэффициент теплопроводности λн. Тепловой источник в этой области отсутствует Р = 0. Область, ограниченная координатами: 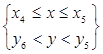 , заполнена наполнителем рабочего объема ЭММА, имеющим постоянный коэффициент теплопроводности λн. Коэффициент теплопроводности определяется в зависимости от состава наполнителя (измельчаемый продукт в смеси с ферромагнитными размольными элементами). Область характеризуется отсутствием теплового источника Р = 0.
, заполнена наполнителем рабочего объема ЭММА, имеющим постоянный коэффициент теплопроводности λн. Коэффициент теплопроводности определяется в зависимости от состава наполнителя (измельчаемый продукт в смеси с ферромагнитными размольными элементами). Область характеризуется отсутствием теплового источника Р = 0.
Область, ограниченная координатами:
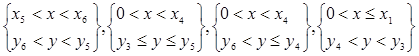 ,
,
заполнена ферромагнитным материалом, имеющим постоянный коэффициент теплопроводности λс. Эта область также не содержит теплового источника Р = 0.
Поскольку уравнение теплопроводности при стационарном режиме в двухмерной модели ![]() не зависит от времени t, то начальные условия отсутствуют.
не зависит от времени t, то начальные условия отсутствуют.
Граничные условия: на поверхности 16 (х = х6, у6 < y < y5), ![]() ; на поверхности 15 (х5 <x ≤ x6 , y = y5),
; на поверхности 15 (х5 <x ≤ x6 , y = y5), ![]() ; на поверхности 15 (х5 <х ≤ х6 , у = у6),
; на поверхности 15 (х5 <х ≤ х6 , у = у6), ![]() ; на поверхности 17 (0 < x ≤ x5, y = y5),
; на поверхности 17 (0 < x ≤ x5, y = y5), ![]() ; поверхность 18 теплоизолирована (х=0, у6 < у ≤ у5);
; поверхность 18 теплоизолирована (х=0, у6 < у ≤ у5); ![]() ; на поверхности 17 (0 < х ≤ х5, у = у6),
; на поверхности 17 (0 < х ≤ х5, у = у6), ![]() (здесь α1, α2, α3 – коэффициенты теплоотдачи на соответствующих поверхностях; υ0 – температура окружающей среды).
(здесь α1, α2, α3 – коэффициенты теплоотдачи на соответствующих поверхностях; υ0 – температура окружающей среды).
В соответствии с обозначениями размеров цилиндрической модели (рисунок 1) выражения для координат имеют вид (рисунок 3.): х1 = R – δu, у1 = 1/2 bk; х2 = R1, y2 = - 1/2 bk; x3 = R2, y3 = 1/2 bk + δu; х4 = R2 + δu, у4 = (1/2 bk + δu); х5 = R3, y5 = 1/2 b; х6 = R4, y6 = -1/2b.
ОУ состоит из медных проводов диаметром dM. Наружный диаметр провода вместе с изоляцией равен du. При заполнении объема круглыми проводами, касающимися друг друга, часть сечения ОУ, равная ![]() , занята сечением проводов, а остальная часть сечения, равная (
, занята сечением проводов, а остальная часть сечения, равная ( ![]() )≈0,1, представляет собой площадь промежутков между проводами. Из площади сечения, занятой проводами, часть площади, равная
)≈0,1, представляет собой площадь промежутков между проводами. Из площади сечения, занятой проводами, часть площади, равная ![]() , занята медью, а остальная часть, равная
, занята медью, а остальная часть, равная ![]() , занята изоляцией. Обозначив коэффициент теплопроводности меди через λM, коэффициент теплопроводности изоляции провода – λип и коэффициент теплопроводности воздуха, заполняющего промежутки между проводами, через λв, эквивалентный коэффициент теплопроводности объема катушки можно приближенно определить по формуле:
, занята изоляцией. Обозначив коэффициент теплопроводности меди через λM, коэффициент теплопроводности изоляции провода – λип и коэффициент теплопроводности воздуха, заполняющего промежутки между проводами, через λв, эквивалентный коэффициент теплопроводности объема катушки можно приближенно определить по формуле:
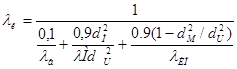 .
.
Обозначим сопротивление катушки возбуждения, вычисленное для максимально допустимой для изоляции ОУ температуры, через Rk. При протекании электрического тока Ι в ОУ будут выделяться тепловые потери Р = I²R. Если объем V, занятый ОУ, определен по формуле ![]() , то тепловой источник Р0 (потери, выделяющиеся в единице объема ОУ) равен
, то тепловой источник Р0 (потери, выделяющиеся в единице объема ОУ) равен ![]() .
.
Коэффициент теплоотдачи αс наружной поверхности зависит от окружной скорости υ соответствующего элемента поверхности устройства и выражается зависимостью ![]() , (здесь α и β́ – постоянный величины). Так как окружная скорость υ элемента поверхности, расположенного на расстоянии r от оси устройства равна
, (здесь α и β́ – постоянный величины). Так как окружная скорость υ элемента поверхности, расположенного на расстоянии r от оси устройства равна ![]() (здесь n – частота вращения соответствующего элемента поверхности ЭММА), то уравнение можно представить в виде:
(здесь n – частота вращения соответствующего элемента поверхности ЭММА), то уравнение можно представить в виде: ![]() . Обозначив
. Обозначив ![]() через β, получим
через β, получим![]() .
.
Половина наружной поверхности 1 превращается при спрямлении в плоскость 16 (рисунок 2), имеющую меньшую площадь. Для сохранения тепловой эффективности поверхности 16 коэффициент теплоотдачи должен быть удвоен обратно пропорционально уменьшению ее площади. Коэффициент теплоотдачи αп поверхности 1 определен по формуле ![]() . Поскольку отношения площадей 1 и 16 равны
. Поскольку отношения площадей 1 и 16 равны 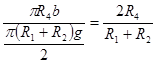 , то коэффициент теплоотдачи α1 поверхности 16 можно представить в виде
, то коэффициент теплоотдачи α1 поверхности 16 можно представить в виде ![]() . Для боковой поверхности 2 средний коэффициент теплоотдачи α4 определен выражением:
. Для боковой поверхности 2 средний коэффициент теплоотдачи α4 определен выражением: 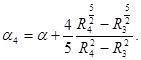 При спрямлении половина боковой поверхности 2 преобразуется в меньшую поверхность 15. Отношение площадей 2 и 15 равны
При спрямлении половина боковой поверхности 2 преобразуется в меньшую поверхность 15. Отношение площадей 2 и 15 равны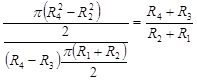 . Для сохранения тепловой эффективности поверхности 15 коэффициент теплоотдачи этой поверхности должен быть получен путем умножения коэффициента α4 на отношение площадей 2 и 15:
. Для сохранения тепловой эффективности поверхности 15 коэффициент теплоотдачи этой поверхности должен быть получен путем умножения коэффициента α4 на отношение площадей 2 и 15: 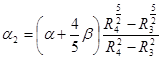 .
.
Половина боковой поверхности 3 устройства при спрямлении увеличивается и превращается в поверхность 17 (рисунок 2). Средний коэффициент теплоотдачи α3 поверхности 3 определен по формуле:
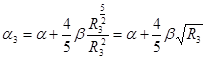 .
.
Для сохранения тепловой эффективности поверхности 17 коэффициент ее теплоотдачи α17 определен в результате умножения площадей поверхностей 3 и 17 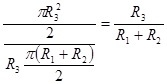 на коэффициент теплоотдачи поверхности
на коэффициент теплоотдачи поверхности ![]() .
.
В расчетах необходимо учитывать изменения площадей поверхностей разрабатываемых устройств. С целью сохранения тепловой идентичности моделей коэффициенты теплоотдачи соответствующих поверхностей спрямленной модели должны быть изменены обратно пропорционально изменению площадей этих поверхностей по сравнению с цилиндрической моделью.
Заключение
Сравнительный анализ параметров теплового поля ЭММА цилиндрических конструкций, полученных экспериментальными исследованиями и теоретическим расчетом на ПК, подтвердили правомерность предложенного метода [13,14]. Метод рекомендован для практических расчетов температурного поля при разработке технических заданий и предложений, эскизных и технических проектов ЭММА, отвечающих требованиям производства по энергетическим и качественным показателям выпускаемой продукции.
Рецензенты:
Салова Т.Ю., д.т.н., профессор кафедры «Энергообеспечение предприятий» СПбГАУ, руководитель ведущей научной и научно-педагогической школы СПб «Системы, узлы и агрегаты двигателей», г. Санкт Петербург;
Ракутько С.А., д.т.н., зав. лабораторией энергоэффективных электротехнологий, ИАИП, г. Санкт Петербург.
Библиографическая ссылка
Беззубцева М.М., Волков В.С. К ВОПРОСУ ИССЛЕДОВАНИЯ ЭНЕРГОЭФФЕКТИВНОСТИ МЕХАНОАКТИВАТОРОВ С МАГНИТООЖИЖЕННЫМ СЛОЕМ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=21336 (дата обращения: 21.01.2026).



