В наше время основное внимание исследователей уделяется большим социальным сетям, изучению их характеристик; межличностные коммуникации рассматриваются также в основном в среде этих сетей, а реальная жизнь и реальные взаимоотношения отошли несколько на второй план. Если рассматривать образовательную сферу, то не все еще курсы в университете электронные, и не все занятия дистанционные, студенты и преподаватели имеют возможность обычного человеческого общения.
Остаются и привычные академические группы, студенты ходят ежедневно на занятия и общаются после занятий. Группы различаются по своей успеваемости, активности в общественной жизни вуза, поэтому вполне уместны такие вопросы, как: группы формируются из абитуриентов, имеющих практически равные оценки по ЕГЭ, они обучаются у одних и тех же преподавателей, почему же в одной группе успеваемость значительно ниже, чем в другой? Почему студенты одной группы продолжают встречаться и поддерживают отношения и после окончания учебы, т.е. группа достаточно устойчива, а в другой даже не здороваются, встретившись на улице?
Есть и более прикладные задачи при изучении таких социальных групп: если возникает необходимость оповещения всей группы о некотором событии, кому в группе лучше передать информацию; или другой случай: при возникновении эпидемии кому в первую очередь нужно ставить прививку?
Члены группы по-разному проявляют себя в группе, имеют разное влияние, играют разные роли. В первую очередь интересны те, кто позиционированы как лидеры, те, кто оказывают наибольшее влияние на характеристики группы. В теории анализа социальных сетей (АСС) такие наиболее важные узлы определены как центральные, а мера этой центральности может быть выражена численно.
В нашем исследовании одной из основных характеристик, которая изучалась, являлась устойчивость группы. Рассматривалось понятие устойчивости с точки зрения теории аутопоэза. Аутопоэтическая система устойчива по определению. Аутопоэз – это свойство системы воспроизводить саму себя, свою структуру (границу) и процессы, а значит устойчиво существовать во времени [5].
Основные понятия SNA
В качестве объектов исследования были выбраны академические группы разных курсов обучения. Исследование проводилось с использованием методологии, известной как SNA–методология (SNA – Social Network Analysis – Анализ социальных сетей). В качестве основного информационного инструмента использовалась пробная версия системы UCINET [4].
SNA-методология является сочетанием социологии, теории сетей и теории графов на базе использования информационных технологий. Центральным ее положением является то, что любая социальная группа представима в виде сети, узлами, которой являются члены группы (называемые акторами); связи, существующие между акторами, изображаются в виде сетевых каналов [2]. Каждая сеть представима графом, поэтому акторы – это в то же время вершины графа, связи - ребра графа. Связь может быть направленной, тогда она отображается в графе дугой (граф является орграфом). Ребро графа может иметь вес, отражающий силу связи.
Используется следующая терминология: если хотят подчеркнуть социальную сторону, то говорят об акторах и связях между ними; если акцент делается на сетевой составляющей, то применяют термины узлы и каналы; а если рассчитываются некоторые топологические характеристики, то говорят о вершинах и ребрах (дугах).
Информационной основой для анализа является социоматрица, являющаяся, по сути, матрицей смежности графа (если ребрам приписаны веса, то это матрица целых чисел).
Уточним некоторые понятия. Маршрутом (walk) в орграфе называется такая конечная или бесконечная последовательность ребер, что каждые два соседних ребра имеют общую концевую точку. Если начальная и концевая точка совпадают, то говорят о замкнутом маршруте (closed walk). В маршруте ребра и вершины могут повторяться.
Маршрут называется цепью (trail), замкнутый маршрут – замкнутой цепью, если каждое ребро этого маршрута встречается в нем не более одного раза. Путем (path) будем называть цепь, в которой нет повторяющихся вершин (или это маршрут, в котором одно и то же ребро и одна и та же вершина может встретиться только один раз). Длина маршрута (цепи/ пути) обычно определяется как количество ребер, входящих в маршрут (цепь/путь), однако если ребра графа имеют вес, длину соответствующего топологического элемента можно вычислять как сумму весов, составляющих его ребер. Замкнутый путь (длиной больше 2) называется циклом.
Маршруты, цепи и пути могут быть определены как для ориентированных, так и для неориентированных графов. В случае ориентированного графа уточняется, принимаются ли направления ребер во внимание при определении этих топологических единиц; в нашем исследовании направление принималось во внимание. Часто говорят о геодезическом расстоянии между двумя вершинами (geodesic path) - как о длине кратчайшего пути, соединяющего эти вершины.
Данные для исследования
Традиционным источником данных о социальных коммуникациях является анкетирование. В данной работе использованы данные, собранные в ходе внедрения системы управления качеством «КОМПАС TQM» [1] в учебный процесс одного из департаментов Уральского федерального университета. Данная система предусматривает обязательное регулярное оценивание студентами результатов взаимодействия с другими студентами, преподавателями, представителями служб университета и любыми другими людьми (или организациями). Оценка выражается в баллах, может быть как положительной, так и отрицательной. Каждая оценка обязательно сопровождается словесным комментарием. Оценки, выставленные друг другу участниками системы, отражают реальные коммуникации между ними и подтверждаются текстами комментариев. Знак оценки («+» или «-») характеризуют общее отношение «получателя информации» к результату данной коммуникации, а ее численное значение (от 1 до 5 баллов) определяет силу данного отношения (например, степень полезности для получателя).
Данные накоплены за год: в течение двух семестров 2013-2014 учебного года студенты, предварительно зарегистрировавшись в системе, вносили оценки своих. Образовано два набора данных (за осенний и за весенний семестры): первый содержит 4846 оценочных записей, второй – 4769. В эксперименте участвовали студенты бакалавриата с 1 по 4 курс, но наиболее активными оказались группы 1 курса в весеннем семестре, и 4 – в осеннем семестре.
Применение данного метода сбора данных имеет неоспоримые преимущества перед анкетированием. Данный метод позволяет получить более объективные данные: сбор данных имеет протяженность во времени, неоднократен, меньше зависит от настроения респондента. Оценка ставится не сразу после коммуникации, а, значит, респондент может более объективно оценить коммуникацию.
Меры центральности
Центральность – это «важность» узла в сети, характеристика его положения по отношению к остальным узлам и сети в целом. Мер, позволяющих оценить центральность, множество: центральность по степени, центральность по близости, центральность по посредничеству, показатель власти по Бонакичу и др.
Можно центральным в группе считать того, кто связан с наибольшим числом членов группы. Эти связи отражаются в показателе центральности по степени, который считается как количество ребер, инцидентных данной вершине. Если исследуется орграф, то говорят о входной центральности по степени (количество входящих в вершину дуг), ее рассматривают и как престижность актора. Выходная центральность по степени (количество исходящих из вершины дуг) отражает влиятельность (иногда говорят экспансивность) актора. Чтобы можно было сравнивать сети разной размерности, эти показатели нормируют (делят на максимально возможное количество связей узла, которое в случае N узлов в сети, равно N-1).
На рис. 1 показан орграф коммуникаций, построенный для академической группы 4 курса. Для построения использована свободно распространяемая система NetDraw 2.152.
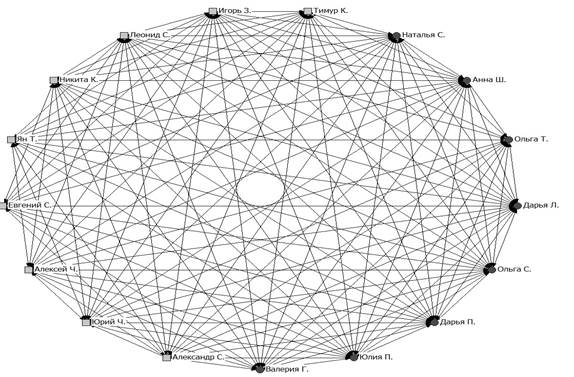
Рис. 1. Орграф коммуникаций академической группы 4 курса (квадратами изображены узлы, которые соответствуют студентам группы, кругами – студенткам).
В таблице 1 приведены различные меры центральности для исследуемой группы 4 курса.
Таблица 1
Меры центральности
|
№ |
Актор |
Выходная цетральность по степени |
Входная центральность по степени |
Входная центральность по степени (баллы) |
Показатель власти по Бонакичу |
Входная центральность по близости |
Выходная центральность по близости |
Центральность по посредничеству |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
Валерия Г. |
0,9375 |
0,75 |
223 |
0,891 |
0,8 |
0,941 |
0,09 |
|
2 |
Игорь З. |
0,875 |
1 |
369 |
1,197 |
1 |
0,889 |
0,21 |
|
3 |
Тимур К. |
0,75 |
0,875 |
276 |
1,029 |
0,889 |
0,8 |
0,124 |
|
4 |
Никита К. |
0,625 |
0,8125 |
228 |
1,043 |
0,842 |
0,727 |
0,094 |
|
5 |
Дарья Л. |
0,5 |
0,9375 |
272 |
1,193 |
0,941 |
0,667 |
0,059 |
|
6 |
Юлия П. |
1 |
0,75 |
201 |
0,877 |
0,8 |
1 |
0,12 |
|
7 |
Дарья П. |
0,8125 |
0,9375 |
190 |
1,208 |
0,941 |
0,842 |
0,253 |
|
8 |
Наталья С. |
0,9375 |
0,8125 |
198 |
0,944 |
0,842 |
0,941 |
0,213 |
|
9 |
Алексей С. |
1 |
0,5625 |
108 |
0,674 |
0,696 |
1 |
0,054 |
|
10 |
Евгений С. |
0,75 |
0,625 |
133 |
0,748 |
0,727 |
0,8 |
0,036 |
|
11 |
Лев С. |
1 |
0,875 |
162 |
1,107 |
0,889 |
1 |
0,18 |
|
12 |
Ольга С. |
1 |
0,75 |
249 |
0,886 |
0,8 |
1 |
0,203 |
|
13 |
Ян Т. |
0,6875 |
0,625 |
288 |
0,825 |
0,727 |
0,762 |
0,021 |
|
14 |
Ольга Т. |
0,4375 |
0,8125 |
210 |
0,983 |
0,842 |
0,64 |
0,036 |
|
15 |
Алексей Ч. |
0,625 |
0,9375 |
275 |
1,130 |
0,941 |
0,727 |
0,107 |
|
16 |
Юрий Ч. |
0,8125 |
0,75 |
256 |
0,837 |
0,8 |
0,842 |
0,129 |
|
17 |
Анна Ш. |
1 |
0,9375 |
174 |
1,197 |
0,941 |
1 |
0,238 |
Во втором и третьем столбцах таблицы приведена нормированная центральность по степени, рассчитанная на основе количества акторов, с которыми установлены связи (входные и выходные). Например, Алексей С. напрямую общается (инициатор общения) со всеми членами группы. Если посмотреть на значения третьего столбца, то таких, как Алексей С., еще 4 человека: Юлия П., Лев С., Ольга С. и Анна Ш., они наиболее влиятельны (активны) в группе. Наиболее «престижными» по своим связям (определяется столбцом 4) в группе можно считать Игоря З., Дарью П., Алексея Ч. и Анну Ш. По двум этим параметрам «звездой» можем считать Анну Ш. (строка 17 в таблице 1). Если рассматривать как основание для подсчета центральности по степени количество полученных баллов (входная центральность по степени), то наибольшее количество баллов в системе получил Игорь З., его можно считать второй «звездой» в группе.
Исследуемая группа по показателям центральности по степени оказалась достаточно равномерной (лидеров несколько): все члены группы вовлечены в коммуникации, нет «изолянтов»; среднее значение как входной, так и выходной центральности 0,8, среднеквадратичные отклонения этих центральностей по входу: 0,12, по выходу: 0,2 (для сравнения те же показатели, рассчитанные для группы первого курса, по входной и выходной центральностям 0,51, а среднеквадратичное отклонение по входу 0,19, по выходу 0,26).
Бонакич (Bonacich) предложил другой подход к измерению центральности узла в сети. Определение центральности по степени основано на том факте, что чем больше связей ты имеешь, тем на большее количество людей можешь непосредственно воздействовать, но в нем не учитывается то, кто на другом конце связи, насколько он «централен». Бонакич предложил учитывать не только, сколько у актора связей, но и насколько эти связи «продуктивные», продуктивность определяется центральностью актора на другом конце связи. Центральность по Бонакичу (часто называемая показателем власти) определяется как взвешенная сумма центральностей акторов, которые с ним связаны, а эти центральности - как суммы взвешенных центральностей тех акторов, которые связаны с ними, и т.д. Как видно из таблицы 1 (5 столбец), по этому показателю наиболее центральна Дарья П., у нее меньше связей, чем у Анны Ш., но они более «продуктивные».
Следующая группа показателей центральности – это показатели центральности по близости. Центральность по близости определяет, насколько данный узел близок ко всем остальным узлам в сети. Рассчитывается как величина, обратная сумме геодезических расстояний (длин кратчайших путей) от данной вершины до всех остальных вершин в сети.
![]() , (1)
, (1)
где d(i,j) – кратчайшее расстояние между вершинами i и j, а N – общее количество вершин (размер сети).
Как и в случае центральности по степени, если граф ориентированный, то можно считать входную (расстояния от всех вершин до рассматриваемой) и выходную (расстояния от рассматриваемой вершины до остальных) центральности по близости. Вассерман и Фауст [7] предложили нормализовать меру:
![]() . (2)
. (2)
Рассчитанные по формуле (2) входная и выходная центральности приведены в 6 и 7 столбце таблицы 1. В группе есть студенты, напрямую связанные со всеми остальными, у них значения центральностей по близости равны единице. Обычно эту меру интерпретируют как показатель скорости распространения информации [3], и самым быстрым способом извещения всех в группе является обращение в узлы с наибольшим показателем выходной близости, а сами сведущими в группе о всех новостях группы являются те, у кого максимальный показатель входной центральности по близости. Самыми удаленными от всех остальных в группе являются: по входу - Алексей С., а по выходу – Ольга Т.
Интересна еще одна мера центральности, она достаточно хорошо показывает сплоченность группы. Она навеяна теорией «малых миров», которая утверждает, что каждый в нашем мире имеет связь с любым другим живущим в данный момент, не более чем при помощи 6 посредников. Называется такая мера Reach Centrality (центральность по доступности) и показывает минимальное количество шагов (или посредников), необходимых каждому, чтобы через установленные связи достичь каждого другого в сети. В этой группе каждый может достичь каждого другого не более чем за 2 шага. Для сравнения: другая группа того же курса имеет показатель доступности 3, у групп первого курса этот показатель равен 4.
Взаимодействие двух не смежных (соседних) акторов может находиться под контролем возможных посредников. Центральность по посредничеству (3) рассчитывается как доля самых коротких путей, соединяющих все пары вершин в сети, которые проходят через данную вершину. Показатель для оргматрицы (без весов) рассчитывается по формуле:
![]() , ( i≠j≠k), (3)
, ( i≠j≠k), (3)
где ![]() – количество кратчайших путей между вершинами j и k;
– количество кратчайших путей между вершинами j и k;
![]() - количество кратчайших путей между вершинами j и k, проходящих через вершину i.
- количество кратчайших путей между вершинами j и k, проходящих через вершину i.
Расчет с учетом весов связей предложен в [6]. Показатель нормализуется делением на максимально возможную величину - (N-1)(N-2)/2.
В исследуемой группе показатели посредничества достаточно низкие, т.к. связи внутри группы довольно тесные, и посредничества не требуется.
Благодаря рассмотренным показателям центральности удалось определить, что данная академическая группа достаточно сплоченная (малый показатель центральности по доступности, практически не нужны посредники при общении) и устойчивая, т.к. в группе не единственный лидер, удаление которого может привести к краху всей структуры группы.
Рецензенты:
Берг Д.Б., д.ф-м.н., профессор, профессор кафедры анализа систем и принятия решений департамента Бизнес-информатики и математического моделирования Высшей школы экономики и менеджмента ФГАОУ ВПО «УрФУ», г. Екатеринбург;
Доросинский Л.Г., д.т.н., профессор, зав. кафедрой теоретических основ радиотехники, ИРИТ-РТФ ФГАОУ ВПО «УрФУ», г. Екатеринбург.
Библиографическая ссылка
Зверева О.М. ИСПОЛЬЗОВАНИЕ МЕР ЦЕНТРАЛЬНОСТИ ПРИ АНАЛИЗЕ АУТОПОЭТИЧЕСКИХ СТРУКТУР В СОЦИАЛЬНЫХ СИСТЕМАХ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=21176 (дата обращения: 01.07.2025).



