В данной работе рассматриваются предложенные автором элементарные гомеостатические модели на сетях Петри и исследуются их поведенческие свойства. Под гомеостазом (от греч. homois – одинаковый и stasis – состояние) понимается свойство системы поддерживать состояние своей «внутренней среды» постоянным вне зависимости от внешних условий. Это понятие было введено Уолтером Кенноном в конце 1920-х гг. в развитие идей великого французского физиолога Клода Бернара и с тех пор быстро распространилось на все области системного анализа, так как оказалось очень удачным для описания сохраняемых свойств сложных систем любой природы [7]. Понятие «внутренняя среда» или «внутреннее состояние» (последнее больше подходит для технических систем) имеет много разных аспектов. В данной работе мы остановимся лишь на таком аспекте, как внутренний ресурс.
Рассматриваемые в работе модели поддерживают свой внутренний ресурс на определенном уровне (в зависимости от законов функционирования системы он может непрерывно увеличиваться, оставаться постоянным или непрерывно колебаться в каких-то пределах) и при вмешательстве извне и изменении ресурса восстанавливают его. При увеличении ресурса система его автоматически понижает, а при уменьшении – увеличивает. Аппарат сетей Петри удобен тем, что его спецификация позволяет описывать системы с различными уровнем сложности, в том числе и биологические системы с клеточным строением и межклеточными связями, которые он напоминает.
Сети Петри определяются как
![]() , (1)
, (1)
где ![]() - конечное множество позиций сети,
- конечное множество позиций сети, ![]() - конечное множество переходов сети,
- конечное множество переходов сети, ![]() - алгебраическое представление сети,
- алгебраическое представление сети, ![]() - начальная маркировка сети.
- начальная маркировка сети.
Простейшая гомеостатическая модель на сетях Петри представлена на рис. 1a.
Это модель, генерирующая маркеры. Ее переходы срабатывают одновременно и являются синхропереходами. Маркировка сети на ![]() -м срабатывании будет иметь в два раза больше маркеров чем на
-м срабатывании будет иметь в два раза больше маркеров чем на ![]() -м.
-м.
Изменение маркировки описывается следующей системой уравнений:
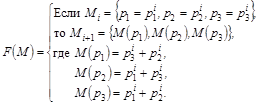
Число редупликаций в позиции является функцией от числа выходящих из неё дуг. В сети на рис. 1 число редупликаций в позиции ![]() , т.е.
, т.е. ![]() .
.
Редупликации маркеров в позициях сети происходят одновременно при срабатывании переходов. Таким образом, для позиции ![]() такой сети при срабатывании переходов, выходящих из данной позиции
такой сети при срабатывании переходов, выходящих из данной позиции ![]() , маркеры данной позиции редуплицируются
, маркеры данной позиции редуплицируются ![]() раз (для модели на рис. 1 число редупликаций равно 1) и приходят по выходящим дугам в соседние позиции, полностью исчезая из родительской.
раз (для модели на рис. 1 число редупликаций равно 1) и приходят по выходящим дугам в соседние позиции, полностью исчезая из родительской.
Таким образом, непрерывно происходит редупликация и обмен маркеров.
Процесс редупликации и обмена маркерами за одно срабатывание сети, приведенной на рис. 1, можно изобразить следующим образом.
Как видим, число маркеров в сети растет по геометрической прогрессии согласно формуле ![]()
![]() .
.
Если на каком-то уровне развития сети (после ![]() -го срабатывания сети) из любой позиции убрать все маркеры, то сеть их вновь регенерирует и восполнит в количестве, в два раза превышающем взятое (рис. 1b, c).
-го срабатывания сети) из любой позиции убрать все маркеры, то сеть их вновь регенерирует и восполнит в количестве, в два раза превышающем взятое (рис. 1b, c).
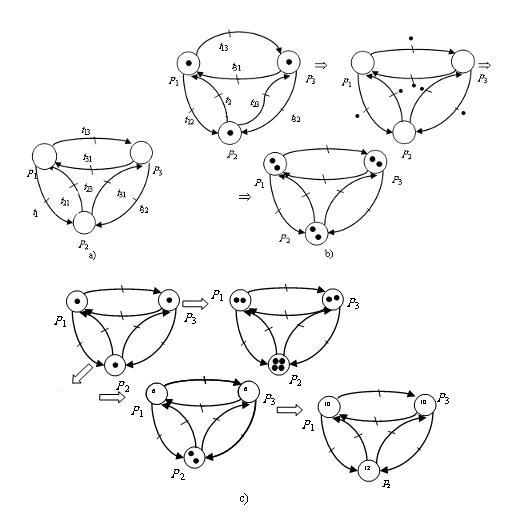
Рис. 1. Гомеостатические модели на сетях Петри.
![]() ,
,
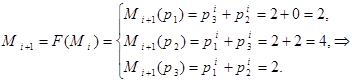
![]() .
.
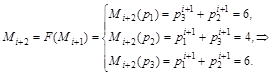
![]() .
.
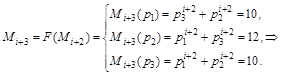
![]() .
.
Однако в данной сети соотношение между количеством маркеров в соседних двух позициях будет отличаться на ![]() и
и ![]() соответственно, где
соответственно, где ![]() и
и ![]() – число маркеров в этих двух позициях в момент воздействия на позицию, соседнюю с ними (рис. 2). Причем оно будет колебаться то в положительном, то в отрицательном направлении.
– число маркеров в этих двух позициях в момент воздействия на позицию, соседнюю с ними (рис. 2). Причем оно будет колебаться то в положительном, то в отрицательном направлении.
Таким образом, получается, что система обладает памятью. Итак, любое воздействие на количество маркеров в системе нарушает соотношение между числом маркеров в соседних позициях.
Заметим, что система регенерирует и при удалении всех маркеров из двух позиций. Для регенерации достаточно всего лишь одной позиции с маркером. Это наблюдение справедливо не только для систем из трех позиций-элементов, но и для системы из ![]() позиций. Единственным условием является лишь наличие связей между всеми элементами (связь все-ко-всем, или
позиций. Единственным условием является лишь наличие связей между всеми элементами (связь все-ко-всем, или ![]() ). Что касается памяти в системах подобного рода, то такую память можно назвать обменной или метаболической.
). Что касается памяти в системах подобного рода, то такую память можно назвать обменной или метаболической.
Если теперь на гомеостаз системы, т.е. на обмен позиций маркерами, наложить ограничение, такое как один переход за одно срабатывание изымает из позиции только постоянное число маркеров ![]() , то соотношение между числом маркеров будет также восстанавливаться.
, то соотношение между числом маркеров будет также восстанавливаться.
В таком случае редупликация в позиции будет возникать не постоянно, при срабатывании сети, а лишь по мере необходимости, когда число маркеров в позиции меньше числа выходящих из неё переходов.
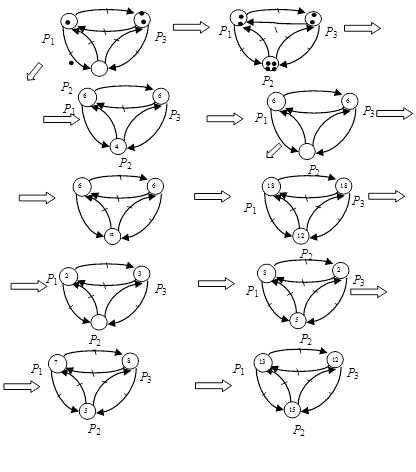
Рис. 2. Изменение соотношения между количеством маркеров в позициях после регенерации.
Подобную сеть (как на рис. 3) назовем сетью со стационарным или постоянным гомеостазом. Изменение маркировки будет описываться следующей системой выражений:
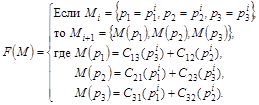
В нашем случае (для сети на рис. 3)
![]() . (2)
. (2)
Как видим, после изъятия маркера из позиции ![]() система восстанавливает состояние между количеством маркеров в позициях, однако количество маркеров в позициях увеличивается до двух и впоследствии сохраняется. Если изъять маркеры из позиции при
система восстанавливает состояние между количеством маркеров в позициях, однако количество маркеров в позициях увеличивается до двух и впоследствии сохраняется. Если изъять маркеры из позиции при ![]() , то число маркеров в позициях уменьшается до двух, а если изъять маркеры из одной позиции при
, то число маркеров в позициях уменьшается до двух, а если изъять маркеры из одной позиции при ![]() для всех позиций, то число маркеров восстановится до прежнего (рис. 4).
для всех позиций, то число маркеров восстановится до прежнего (рис. 4).
Таким образом, в подобных сетях восстановление числа маркеров в сети до двух обусловлено числом входящих дуг и пропускной способностью переходов этих дуг.
![]()
![]()
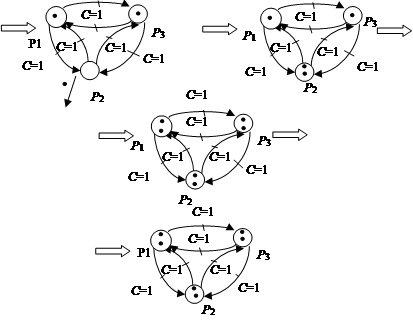
Рис. 3. Сеть со стационарным гомеостазом.
![]() (3)
(3)
Избыток маркеров в какой-либо позиции, из-за ограничения на пропускную способность перехода, по соседним позициям не распределяется. Поэтому сеть является сохраняющей.
Таким образом, в силу формулы (3) при ![]() сеть регенерирует число маркеров в позициях до двух, а при
сеть регенерирует число маркеров в позициях до двух, а при ![]() сеть перераспределяет маркеры до такого распределения, что
сеть перераспределяет маркеры до такого распределения, что ![]() . Условие
. Условие ![]() можно определить как условие неизбыточности.
можно определить как условие неизбыточности.
Вышесказанные системы являются самовосстанавливающимися. Система на рис. 3 обладает действительно стационарным гомеостазом (обменом маркерами), а вот система на рис. 1 обладает непрерывно увеличивающимся обменом маркерами (рис. 2), т.е. её состояние меняется и поэтому её нельзя назвать гомеостатической в принятом понимании этого термина. Однако если считать её нормальным состоянием непрерывную генерацию маркеров и соответственно непрерывно увеличивающийся обмен, то в таком аспекте о гомеостатичности говорить можно. Система на рис. 4 также является лишь квази-гомеостатической, так как, несмотря на постоянный объем обмена маркерами, избыточные маркеры из позиций не удаляются. Полностью гомеостатической системой можно назвать только модель на рисунке 5.
![]()
![]()
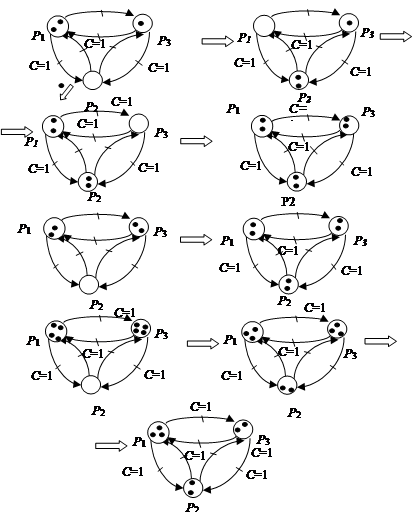
Рис. 4. Сеть со стационарным гомеостазом с ограничением на пропускную способность переходов С=1.
Рис. 5. Полностью гомеостатическая сеть.
Эта сеть отличается от предыдущей тем, что имеет ингибиторные дуги, которые регулируют поток избыточных маркеров из позиций. Переходы, снимающие избыточность из позиций, или оттоковые переходы ![]() , срабатывают лишь после того, как сработают основные переходы
, срабатывают лишь после того, как сработают основные переходы ![]() , т.е. после того как с маркеров
, т.е. после того как с маркеров ![]() -й позиции необходимые для обмена маркеры из нее будут взяты и попадут в переходы
-й позиции необходимые для обмена маркеры из нее будут взяты и попадут в переходы ![]() и
и ![]() , но ещё не перейдут через них. Как видим, она полностью восстанавливает свое внутреннее состояние, удаляя линии - избыточные маркеры. В случае недостатка маркеров в позиции (когда
, но ещё не перейдут через них. Как видим, она полностью восстанавливает свое внутреннее состояние, удаляя линии - избыточные маркеры. В случае недостатка маркеров в позиции (когда ![]() , т.е. в позиции один маркер) сеть редуплицирует его так же, как и сеть со стационарным гомеостазом на рис. 5.
, т.е. в позиции один маркер) сеть редуплицирует его так же, как и сеть со стационарным гомеостазом на рис. 5.
Таким образом, рассмотрены основные типы элементарных гомеостатических моделей на сетях Петри, первая из которых является генеративной, а последние две стационарными. Первые две являются квазигомеостатическими, а последняя полностью гомеостатической.
Исследованы их поведенческие свойства. Модели обладают регенеративными свойствами и редуплицируют маркеры в случае необходимости, что определяется условиями, наложенными на переходы.
Работа выполнена при поддержке РФФИ, проект № 14-07-00143 а.
Рецензенты:
Охоткин Г.П., д.т.н., профессор, заведующий кафедрой автоматики и управления в технических системах ФГБОУ ВПО «Чувашский государственный университет имени И.Н. Ульянова», г. Чебоксары;
Славутский Л.А., д.ф.-м.н., профессор кафедры автоматики и управления в технических системах ФГБОУ ВПО «ЧГУ им. И.Н. Ульянова», г. Чебоксары.
Библиографическая ссылка
Желтов П.В. ГОМЕОСТАТИЧЕСКИЕ МОДЕЛИ НА СЕТЯХ ПЕТРИ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=21155 (дата обращения: 15.11.2025).



