Существующие информационные системы поддержки принятия решений в условиях неопределенности, как правило, используют неигровые алгоритмы, например методы анализа иерархий, методы иерархических сетей, теорию нечеткости, теорию полезности, статистические методы и пр., что ограничивает возможность их применения.
Однако в наши дни в различных социально-экономических сферах деятельности человека часто возникают задачи принятия решений в условиях конфликтов и конкурентной борьбы, когда несколько в общем случае рационально действующих субъектов осуществляют коллективное принятие решений, причем выигрыш каждого зависит не только от выбранной им стратегии, но и от решений других участников и результатов экспериментов. Поэтому необходима разработка и обоснование оптимальных вариантов принятия решений при управлении силами и средствами, действующих в условиях неопределенности, что также приемлемо для воинских формирований [2].
Применение статистических критериев принятия решений в условиях полной неопределенности
Современные воинские формирования — сложные системы, состоящие из множества взаимосвязанных военных объектов. Если число таких объектов возрастает по линейному закону, то число связей между ними увеличивается, по крайней мере, по квадратичному закону. В таких условиях даже талантливому военному руководителю трудно или просто невозможно осуществлять эффективное руководство боевой подготовкой или боевыми действиями без привлечения новейших достижений науки и вычислительной техники.
Потребность управления сложными военными и экономическими (производственными) объектами вызвала к жизни специальные методы, облегчающие принятие правильных решений. Эти методы сейчас принято объединять термином «прикладная математика». Математика со времени своего появления в той или иной степени всегда находила применение в военном деле. Основанный на различных математических методах комплекс расчетных задач способен оказать прямое содействие командованию и штабам при нахождении ответов на определенную группу вопросов, которые могут возникнуть на всех этапах подготовки и ведения боевых действий [5].
Прогнозирование как особый метод научного познания играет важную роль в управлении войсками, особенно в принятии решения, так как данные прогнозирования составляют научную базу любого решения [3].
С происходящим в последнее время усложнением задач и функций руководства силами и средствами роль и значение управленческой информации непрерывно возрастает. Более того, в современных условиях влияние информационного превосходства на ход и исход боя становится соизмеримым с влиянием превосходства в силах и средствах, а в ряде случаев может даже превосходить его [4].
Практические ситуации, в которых приходится принимать военные решения, бывают настолько сложными, что даже незначительная помощь со стороны математических методов является весьма существенной. Известно, что математика и особенно новые ее разделы, сведенные в понятие «исследование операций», возникли и развивались из потребностей практики, в том числе и практики военного дела [1].
В боевых условиях всегда будет иметь место наличие неполной, недостоверной, противоречивой информации (и даже дезинформации), когда исходные данные будут частично, а иногда и полностью отсутствовать или в лучшем случае поступят в органы управления в форме интервальных значений типа «от., до...» либо в форме «с вероятностью не менее....», «предположительно ...», «примерно ...», «не менее....», «не далее ...», «до ...» и др. [4].
Необходима разработка путей и способов решения этой проблемы для удовлетворения современных и особенно перспективных требований к управлению войсками. В частности, на первый план выходит решение задачи количественной оценки ценности информации, используемой в процессах управления, причем в качестве показателя ценности предлагается применять значения, зависящие от степени определенности, конкретности, данных показателей полноты и своевременности.
Необходимо отметить, что следующую сложность при принятии решений в условиях неопределенности представляет то обстоятельство, что, выбирая один из возможных вариантов действий, лицо, принимающее решение (ЛПР), как правило, не имеет необходимой информации о конкретном состоянии среды (условиях обстановки), т. е. ЛПР должен выбирать необходимые ему значения, не зная значений принимаемой противоборствующей стороной, хотя понятно, что исход действий может зависеть от фактического состояния среды [4].
Особенностями оценки сложных систем в условиях неопределенности являются:
1. Наличие в управляющей системе в качестве элемента ЛПР, осуществляющему управление на основе субъективных моделей, которые приводят к большому разнообразию поведения системы.
2. Алгоритм управления строит сама система управления, преследуя помимо целей старшей системы свои цели, не всегда совпадающие с внешними.
3. На этом этапе оценки ситуации в ряде случаев исходят не из фактической ситуации, а из той модели, которую использует ЛПР.
4. В процессе принятия решений большую роль играют логические рассуждения ЛПР, не поддающиеся формализации классическими методами математики.
5. При выборе управляющего воздействия ЛПР может оперировать нечеткими понятиями, отношениями и высказываниями.
Таким образом, методы принятия решений, используемые для детерминированных и вероятностных решений, для данного класса задач неприменимы. В зависимости от характера неопределенности операции делятся на игровые и статистические. В игровых операциях неопределенность вносит своими сознательными действиями противник (теория игр).
Условия статистически неопределенных операций зависят от объективной действительности (природы). Природа пассивна по отношению к лицу, принимающему решение – теория статических решений [6].
Проблема проведения расчетов и принятия обоснованных решений в условиях неопределенности требует безотлагательной и дальнейшей глубокой разработки ее военно-прикладных аспектов, причем не только в научных целях, но и для практического использования в работе командиров и штабов различных воинских формирований.
Расчеты информационных потенциалов воинских формирований и показателей превосходства в общем уровне управления, сейчас не могут считаться адекватными, если при их вычислении не учитывается степень неопределенности данных. В рассматриваемой проблеме применительно к управлению можно выделить следующие важнейшие вопросы:
выявление возможных вариантов проявления неопределенности: неполноты, нечеткости и противоречивости данных;
разработка количественных характеристик степени неопределенности;
разработка методов обработки нечетких данных об одном и том же объекте;
исследование применимости современной критериальной основы и математических методов для выработки оптимальных решений по применению формирований в условиях неопределенности о действиях и намерениях противника [4].
Необходимо отметить, что имеются принципиальные различия между стохастическими факторами, приводящими к принятию решения в условиях риска, и неопределенными факторами, приводящими к принятию решения в условиях неопределенности. И те, и другие приводят к разбросу возможных исходов результатов управления. Но стохастические факторы полностью описываются известной стохастической информацией, эта информация и позволяет выбрать лучшее в среднем решение. Применительно к неопределенным факторам подобная информация отсутствует.
В общем случае неопределенность может быть вызвана либо противодействием разумного противника, либо недостаточной осведомленностью об условиях, в которых осуществляется выбор решения.
Принятие решений в условиях разумного противодействия является объектом исследования теории игр. Необходимо рассмотреть принципы выбора решений при наличии недостаточной осведомленности относительно условий, в которых осуществляется выбор.
Такие ситуации принято называть «играми с природой». Теория статистических решений предлагает несколько критериев оптимальности выбора решений [6].
«Природа» рассматривается как сторона, поведение которой неизвестно, но не содержит элемента сознательного противодействия нашим планам. П. И. Иванов утверждает, что возможные состояния природы (ее стратегии) реализуются случайным образом. В теории статистических решений ЛПР часто называют статистиком, a сами операции - статистическими играми [5].
Рассмотрим возможную критериальную основу принятия решений в условиях неопределенности. Под критерием принятия решений принято понимать некоторую функцию предпочтения, предназначенную для лица, принимающего решение, и определяющую правило выбора оптимального (или целесообразного) варианта решения. В настоящее время в общей теории принятия решений в условиях неопределенности наиболее часто рассматривают четыре наиболее распространенных типа критериев полезности принимаемых решений: критерий Байеса—Лапласа, критерий Вальда; критерий Севиджа, критерий Гурвица. Выбор критерия определяется стратегией (поведением) лица, принимающего решение, его субъективной оценкой ситуации.
Перед рассмотрением сути каждого критерия данные, необходимые для принятия решения, задаются в форме матрицы принятия решений (фактически матрицы эффективности вариантов действий), строки которой соответствуют вариантам действий, столбцы — возможным состояниям обстановки (ситуации), а ее элементы равны значениям целевой функции (т. е. результатам или эффективности) при действиях по определенному варианту решения в различных ситуациях (состояниях обстановки). При этом из матрицы должны быть исключены доминирующие (заведомо выгодные и заведомо невыгодные по всем элементам) строки и столбцы [4].
Применение приведенных выше критериев рассмотрим на следующем условном и упрощенном для наглядности примере выбора наиболее целесообразного варианта действий при принятии решения. Исследования проводились на примере инженерно-аэродромной службы, где в качестве сил и средств использовались инженерно-аэродромные части, которые должны выполнять свою задачу в условиях неопределенности.
По теории статистических решений инженерно-аэродромная служба принимается в качестве статиста. Для выполнения задач по предназначению определены объемы работ, которые должны выполнить инженерно-аэродромные части, в матрице исходных данных они записываются в столбцах (возможные условия). Варианты различных ситуаций (состояний обстановки) использовались в строках матрицы (действия противоборствующей стороны).
Задача состоит в определении такой стратегии (чистой или смешанной), которая при ее применении обеспечила бы инженерно-аэродромной службе наибольший выигрыш.
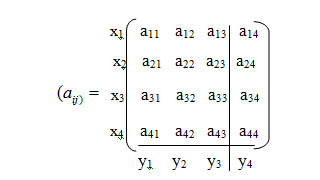
Первым шагом решения задачи исследования было упрощение платежной матрицы (1), которая состояла в выявлении подчиненных или дублирующих стратегий и их отбрасывании. Однако редуцирование матрицы осуществляется только за оперирующую сторону.
Путем исключения неактивных стратегий, получаем в результате выигрыш (2):
![]() (2)
(2)
На втором шаге при недостаточной осведомленности об условиях (о противоборствующей стороне), в которых осуществляется выбор решения, строим платежную матрицу, дополняем исходную матрицу столбцом максимумов построчных элементов и получаем расширенную матрицу.
Далее, используя зависимость ![]() , вычисляем значения
, вычисляем значения ![]() и получаем платежную
матрицу. Затем добавляем дополнительно правую колонку
и получаем платежную
матрицу. Затем добавляем дополнительно правую колонку ![]() и получаем расширенную
платежную матрицу. Из анализа полученных результатов получаем минимальный
критерий среднего выигрыша.
и получаем расширенную
платежную матрицу. Из анализа полученных результатов получаем минимальный
критерий среднего выигрыша.
Индикатором оптимальности принятия решения в условиях статистической неопределенности выступает группа статистических критериев, рассмотрим механизм их работы:
1. В платежной матрице![]() нет доминирующих стратегий, поэтому ее упрощаем.
нет доминирующих стратегий, поэтому ее упрощаем.
2. Платежная матрица неполна и не отражает достоинств и недостатков каждого решения. Поэтому возникает потребность ввести дополнительные показатели, они необходимы, для отражения степени удачности или неудачности выбора стратегии в нашей ситуации.
3. С этой целью выполняем операции для критерия риска.
4. Используем группу критериев, которые должны выступать индикатором оптимальности в условиях полной статистической неопределенности.
По критерию Вальда лица, принимающие решения, выбирают стратегию, гарантирующую максимальное значение наихудшего выигрыша (критерия максимина) (3):
![]() (3)
(3)
Принимающий решение в этом случае минимально готов к риску, предполагая максимум негативного развития состояния внешней среды и учитывая наименее благоприятное развитие для каждой альтернативы.
В соответствии с критерием Сэвиджа в качестве оптимальной выбирается такая стратегия, при которой величина риска принимает наименьшее значение в самой неблагополучной ситуации (4):
![]() (4)
(4)
Расчёт минимакса состоял их четырёх этапов. Выбираем решение, при котором максимальное отклонение будет меньше других.
Разработка программного продукта выполнена на основе алгоритма нахождения наименьшего (наибольшего) значения каждой из альтернатив.
На практике достаточно часто полезно применять все критерии, но поочередно, после чего лицо, принимающее решение, с использованием полученных рекомендаций и дополнительных данных, «волевым» способом принимает окончательное решение.
Заключение
Таким образом, проведенный нами анализ позволил получить поддержку и обоснование принятия решения должностными лицами инженерно-аэродромной службы.
Рассмотрение вопроса об обосновании оптимальных вариантов принятия решений при управлении силами и средствами, действующих в условиях неопределенности целесообразно завершить напоминанием о том, что проблемы могут решаться и на основе других методик, когда известны априорные вероятности возможных ситуаций (состояний обстановки).
Рецензенты:Сидоркин А.Ф., д.ф.-м.н., профессор, заведующий кафедрой физики и химии Военного учебно-научного центра Военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», г. Воронеж;
Сумин А.И., ,д.ф.-м.н., профессор, заведующий кафедрой математики Военного учебно-научного центра Военно-воздушных сил «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», г. Воронеж.
Библиографическая ссылка
Власов А.Б., Мещеряков В.И., Перунов А.Г., Салов С.В. ОБОСНОВАНИЕ ОПТИМАЛЬНОГО ВАРИАНТА ПРИНЯТИЯ РЕШЕНИЙ ПРИ УПРАВЛЕНИИ СИЛАМИ И СРЕДСТВАМИ, ДЕЙСТВУЮЩИХ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=21022 (дата обращения: 18.11.2025).



