Конопля (Cannabissativa, L) – уникальный источник экологически чистых высокорентабельных биопродуктов широкого народного потребления [8]. На международном совещании, проведенном в 1998 г. в Санкт-Петербурге, она была названа культурой ХХI века наравне с пшеницей и соей [10]. По мнению экспертов, в настоящее время из нее можно изготовить более 50 тыс. видов продукций [1]. Поэтому на Западе конопля входит в круг интересов не только частного бизнеса, но для нее создаются и крупные правительственные программы [3]. Сегодня лидерами по производству конопли являются Китай, Канада, Франция, Германия, Италия и США.
Вместе с тем следует обратить внимание на то, что единственным и основным недостатком конопли является наличие в ней наркотического вещества тетрагидроканнабинола (ТГК), оказывающего эйфорическое воздействие на нервную систему человека [4]. В настоящее время распространение наркомании специалистами-медиками оценивается как одна из серьезнейших угроз существования нации. По данным Всемирной организации здравоохранения из более 8 млн жителей Земли, регулярно употребляющих наркотики, более 2 млн проживает в России. А по данным Минздрава Российской Федерации около полумиллиона российских граждан состоит на учете в наркодиспансерах [5]. Но реальные цифры значительно выше: 1,0–1,5 млн в целом по стране наркотически зависимых, а число употребляющих наркотики без проявления болезненной зависимости – 3,0–5,0 млн. Следовательно, исследования по селекции безнаркотических форм конопли должны быть продолжены, и такую работу следует рассматривать в качестве одной из мер борьбы с распространением наркомании [7].
Цель исследований
Целью наших исследований является создание модели сорта безгашишной конопли с помощью генетического алгоритма.
Методика исследований
Работы по гибридизации (простые и сложноступенчатые скрещивания) проводили в полевых условиях. Способ посева широкорядный: расстояние между рядками 60 см, между растениями в рядках – 15 см. В начале цветения материнского сорта изолировали пергаментными изоляторами отдельные растения. Через 20 дней после этого снимали изоляторы, удаляли семена, успевшие завязаться до изоляции, и опыляли соцветия кисточкой. Растения снова накрывали изоляторами, под которыми они находились до самой уборки гибридных семян. Пыльцу для опыления собирали с растений, выращенных в полевых условиях с учетом пространственной изоляции; хранили ее при комнатной температуре в эксикаторе над хлористым кальцием, поместив в темное место.
Изучение гибридов конопли по биологическим и хозяйственно-ценным признакам осуществляли в оценочном питомнике, где гибриды каждого варианта высевали по 2–4 рядка так, чтобы они находились между исходными сортами. Длина каждого рядка составляла 150 см, расстояние между рядками – 45 см, а между растениями в рядках – 5 см. В оценочном питомнике проводили фенологические наблюдения, изучали особенности развития гибридов разных поколений в сравнении с исходными формами. Во время полного цветения гибридов и исходных форм отбирали пробы по 30 растений с целью проведения морфологического анализа стеблей и определения хозяйственно-ценных признаков.
В экспериментах, выполненных в условиях оценочного и контрольного питомника, а также селекционного сортоиспытания, использовали методики, общепринятые в научно-исследовательских учреждениях и Государственном сортоиспытании [6].
Генетический алгоритм — это простая модель эволюции в природе, реализованная в виде компьютерной программы. В нем используются как аналог механизма генетического наследования, так и аналог естественного отбора. При этом сохраняется биологическая терминология в упрощенном виде (рис. 1)
Как моделируется генетическое наследование, показано на рисунке 1.

Рис. 1. Модель генетического наследования
Чтобы смоделировать эволюционный процесс, сгенерируем вначале случайную популяцию — несколько растений со случайным набором генотипов (числовых векторов). Генетический алгоритм имитирует эволюцию этой популяции как циклический процесс скрещивания растений и смены поколений (рис. 2).
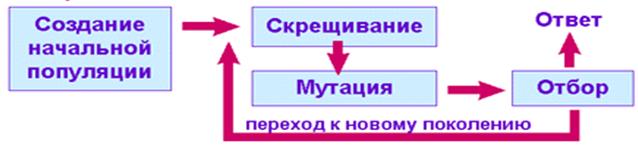
Рис. 2. Алгоритм вычислений
Жизненный цикл популяции — это несколько случайных скрещиваний (посредством кроссовера) и мутаций, в результате которых к популяции добавляется какое-то количество новых растений.
Отбор в генетическом алгоритме — это процесс формирования новой популяции из старой, после чего старая популяция погибает. После отбора к новой популяции опять применяются операции кроссовера и мутации, затем опять происходит отбор, и т.д.
Отбор в генетическом алгоритме тесно связан с принципами естественного отбора в природе следующим образом (рис. 3).

Рис. 3. Принцип естественного отбора в природе
Таким образом, модель отбора определяет, каким образом следует строить популяцию следующего поколения. Как правило, вероятность участия растения в скрещивании берется пропорциональной его приспособленности. Часто используется так называемая стратегия элитизма, при которой несколько лучших растений переходят в следующее поколение без изменений, не участвуя в кроссовере и отборе. В любом случае каждое следующее поколение будет в среднем лучше предыдущего. Когда приспособленность растений перестает заметно увеличиваться, процесс останавливают и в качестве решения задачи оптимизации берут наилучшее из найденных растений.
Возвращаясь к задаче оптимального распределения инвестиций, поясним особенности реализации генетического алгоритма в этом случае.
- Растение = вариант решения задачи = набор изn генотипов Хj
- Генотип Хj= объем вложения в проект j = 16-разрядная запись этого числа
- Так как объемы вложений ограничены, не все значения генотипа являются допустимыми. Это учитывается при генерации популяций.
- Так как суммарный объем инвестиций фиксирован, то реально варьируются только n-1 хромосом, а значение n-ой определяется по ним однозначно.
Результаты исследований и их обсуждение
Известно, что конопле как перекрестноопыляемой культуре присуща очень высокая степень изменчивости признаков; именно по этой причине, даже при соблюдении всех агротехнических требований возделывания, по мере снижения репродукции высеваемых семян происходит ухудшение сортовой типичности, а также уменьшение урожайности стеблей, семян и волокна [2] .
Генетический алгоритм будет состоять из следующих шагов.
1. Генерация начальной группы. В качестве параметров используется битовая строка из 25 элементов. Строка логически разбивается на 5 равных частей по 5 бит, каждая из которых отвечает за определенные параметры. Начальная группа состоит из n растений, генотипы которых измерены в идеальных условиях.
2. Вычисляется значение фитнес-функции каждого растения, по которому производится сортировка. В качестве фитнес-функции можно взять значение максимизируемой функции, так как она удовлетворяет требованиям, предъявляемым к фитнес-функции (неотрицательна, значение фитнес-функции лучших особей больше).
3. Выбор пары растений для скрещивания. Выбор происходит посредством метода рулетки. Для каждого растения вычисляется отношение ее значения функции совокупности параметров к суммарному значению функции совокупности параметров. В зависимости от этого значения растению выделяется некоторое количество ячеек в массиве рулетки. Выбор растений для составления пары происходит независимо в результате двух последовательных запусков рулетки.
4. К выбранной на предыдущем шаге паре растений применяется оператор одноточечного кроссинговера. Точка кроссинговера выбирается равновероятно, случайным образом. Из полученных гибридов случайным образом выбирается один, который добавляется в новую популяцию.
5. Повторение пп. 2–3 n раз. В результате на этом этапе получаем новую группу из n растений. Поскольку выбор родителей производится по числу растений в группе (n раз), велика вероятность того, что в новую группу попадет большое количество гибридов скрещивания наиболее удачных растений. Однако у более слабых растений остается шанс попасть в новую группу, а значит, меньше шанс «потерять» хорошие признаки, присущие в целом не самым удачным растениям.
6. Этап мутации. Каждое растение из новой группы мутирует с вероятностью K%. Следовательно, оператор мутации применяется к K% растений. Оператор мутации заключается в инвертировании случайно выбранного показателя в генотипе растения.
7. В соответствии с логикой элитного отбора добавим в новую группу T% лучших растений прошлого поколения. Для этого отсортируем новую группу по значению фитнес-функции и будем последовательно просматривать T% слабейших растений. Растение заменяется на элитное (гибридное) из прошлого поколения только в случае выигрыша в значении фитнес-функции, т.е. замена происходит, если текущее растение не превосходит по значению фитнес-функции то, на которое его предполагается заменить.
8. Пункты 2–6 выполняются некоторое заранее определенное число раз (m) [2].
Селекционную работу по созданию генетически чистой однодомной конопли, однородной по признаку «идеальной однодомности», проводили по нижеследующей схеме (рис. 4).
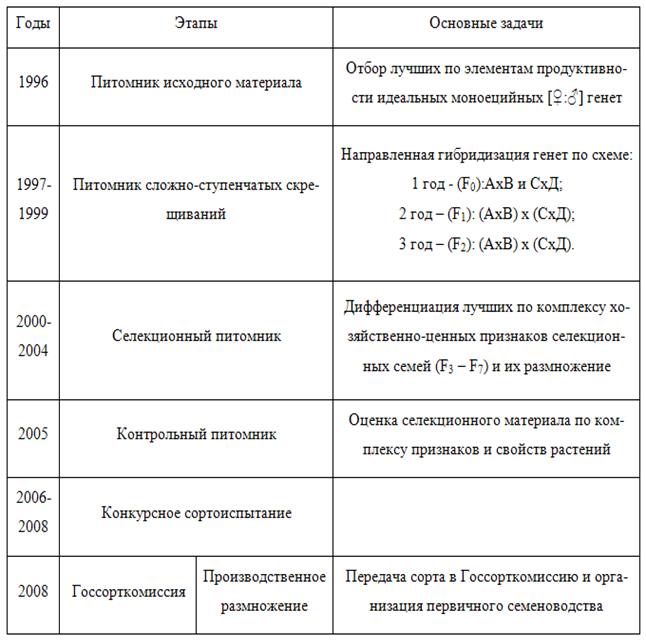
Рис. 4. Схема селекционного процесса однодомной конопли
Выводы
На основе рассмотренных принципов и особенностей был построен генетический алгоритм, позволяющий находить максимум целочисленной функции и получать модель нового сорта.
Проведенные численные эксперименты подтвердили способность генетического алгоритма находить решения, максимально приближенные к наилучшим, избегая попадания в локальные максимумы. Подтверждено и то, что генетический алгоритм позволяет достаточно быстро и с высокой точностью находить ответ на задачи, решение которых переборными методами занимает значительное время.
Таким образом, генетические алгоритмы являются универсальным и эффективным средством для создания моделей сортов, что обусловлено перспективностью принципа эволюции, лежащего в их основе.
Рецензенты:
Игнатьев Н.Г., д.б.н., профессор кафедры агрохимии и экологии ФГБОУ ВПО «Чувашская государственная сельскохозяйственная академия», г. Чебоксары.
Васильев О.А., д.б.н., профессор кафедры землеустройства и кадастров ФГБОУ ВПО «Чувашская государственная сельскохозяйственная академия», г. Чебоксары.
Библиографическая ссылка
Димитриев В.Л., Елисеев И.П., Гурьев А.А. СОЗДАНИЕ МОДЕЛИ СОРТА БЕЗГАШИШНОЙ КОНОПЛИ С ПОМОЩЬЮ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=20999 (дата обращения: 06.02.2026).



