Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Димитриев А.П. 1

---

1 ФГБОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова»

В работе исследовано применение к решению задачи коммивояжера одного из алгоритмов, предложенных автором для дискретной оптимизации в имитационной модели расписания учебных занятий, где данный алгоритм достигает наилучших результатов среди всех известных алгоритмов. При адаптации к задаче коммивояжера указанный алгоритм достигает результатов, сравнимых с результатами метода имитации отжига, а в некоторых случаях превосходящих их. Адаптация состоит в основном в выборе эвристики и формулировке понятия последовательности. Разработана компьютерная программа в свободно распространяемой системе программирования Turbo Delphi 2006, реализующая данный алгоритм и для сравнения другие алгоритмы. В качестве исходных данных для этой программы используются хорошо известные наборы данных. Программа использует несколько параметров, корректируемых пользователем. Приводится пример экранной формы, который иллюстрируют работу программы. Результаты экспериментов сведены в таблицу.

Статья в формате PDF

154 KB

алгоритм

оптимизация

задача коммивояжера

имитация отжига

1. Димитриев А. П. Модели и алгоритмы в системах автоматизированного перевода текста // Прикладная информатика. 2013. № 6 (48). С. 45–59.

2. Сетевые методы решения задачи коммивояжера / М. Г. Булашкова, А. Н. Ломакина, Е. А. Чаузова, С. А. Зотова // Успехи современного естествознания. – 2012. – № 5. – С. 72-73. URL: www.rae.ru/use/?section=content&op=show_article&article_id=9999317 (дата обращения: 19.06.2015).

3. Hentenryck P. V., Vergados Y. Population-based simulated annealing for traveling tournaments. In Proceedings of the 22nd AAAI Conference on Artificial Intelligence, 2007. P. 267–271.

4. Lamartin J. P., Martins J. S. B. AntBeePath: A Hybrid Bio-Inspired Algorithm for Path Determination // AAAI Technical Report FS-12-04 Human Control of Bioinspired Swarms. P. 38 43. URL: https://www.aaai.org/ocs/index.php/FSS/FSS12/paper/viewFile/5598/5834 (accessed 22.05.2015).

5. Particle swarm optimization-based algorithms for TSP and generalized TSP / X. H. Shi, Y. C. Liang, H. P. Lee, C. Lu, Q. X. Wang // Information Processing Letters 103(5). 2007. P. 169-176. URL: https://svn-d1.mpi-inf.mpg.de/AG1/MultiCoreLab/papers/ShiLiangLeeWang07%20-%20PSO%20based%20algorithms%20for%20TSP.pdf (accessed 22.05.2015).

6. Reinelt G. TSPLIB, a traveling salesman problem library. ORSA J. Comput. 1991. № 3. P. 376–384. URL: http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/ (accessed 22.05.2015).

7. Solving the Traveling Tournament Problem by Packing Three-Vertex Paths / M. Goerigk, R. Hoshino, K.-i. Kawarabayashi, S. Westphal // Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence. P. 2271–2277.

8. Sutton A. M., Neumann F. A. Parameterized Runtime Analysis of Evolutionary Algorithms for the Euclidean Traveling Salesperson Problem // Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence. P. 1105–1111.

9. Weiqi Li. Seeking global edges for traveling salesman problem in multi-start search. J Glob Optim. 2011. № 51. P. 515-540. DOI 10.1007/s10898-010-9643-4.

Задача коммивояжера уже около 100 лет привлекает внимание исследователей по дискретной математике по всему миру [2– 9]. Задача коммивояжера – найти кратчайший маршрут, по которому он сможет посетить все требуемые города по одному разу и вернуться в пункт отправления. Существуют разновидности этой задачи. В данной работе рассмотрена симметричная задача (когда расстояния между городами в прямом и обратном направлении одинаковы), геометрическая (расстояния между городами отражают расстояния между точками на плоскости), метрическая (выполняется неравенство треугольника). Задача относится к классу NP-полных задач, т.е. ее решение методом рассмотрения всех вариантов невозможно из-за экспоненциального роста числа вариантов даже при небольшом увеличении числа городов.

В последние десятилетия для решения этой задачи применяются наряду с давно известными методами, такими как жадный алгоритм, метод ветвей и границ, также метаэвристические алгоритмы:

1) метод множественного старта [9];

2) метод роя частиц [5];

3) генетический алгоритм [8];

4) гибридные (например, поиска с запретами и целочисленного программирования [7]);

5) метод имитации отжига [3];

6) метод муравьиной колонии [4] и иные, менее известные.

В работе [1] предложен ряд алгоритмов, которые успешно применялись, в частности, для оптимизации в имитационной модели расписания учебных занятий. Названий они не имели, только нумеровались. Последний из алгоритмов в статье [1] назовем алгоритмом оптимизации последовательности отбора. Он достигал наилучших результатов среди всех предложенных алгоритмов, а также ряда известных алгоритмов: генетических, имитации отжига, множественного старта и их комбинаций. Впоследствии было также определено, что результаты лучше, чем результаты методов роя частиц и муравьиной колонии. В связи с этим предполагается, что он будет эффективно работать и с другими оптимизационными задачами.

Цель работы – рассмотреть применение алгоритма оптимизации последовательности отбора к решению задачи коммивояжера.

Адаптация алгоритма оптимизации последовательности отбора к решению задачи коммивояжера

В исходном виде алгоритм оптимизации последовательности отбора [1] применен к задаче размещения (расположения объектов на временной шкале), которая имитирует составление учебного расписания. Алгоритм заключается в имитации отжига, но не самого размещения, как это обычно делается, а последовательности применения данных об объектах для эвристики размещения, основанной на исследовании локальной области. При этом параметр «температура», обозначаемый T, имеет тот же смысл, что и ранее. Применим алгоритм к задаче коммивояжера, в которой множество городов обозначим G = {gi, 1 ≤ i ≤ n}, где n – количество городов.

Во-первых, определим соответствующую локальную эвристику. В качестве данной эвристики в работе применен метод ближайшего соседа, т.е. при выборе следующего города gi+1 в маршруте выбирается тот, который ближе всего к текущему городу gi, где 1 ≤ i < n. Расстояние между gi и gi+1 обозначим Δi. Задачи выбора следующего города от gn нет, так как это всегда g1.

Во-вторых, определим, что означает последовательность. Для этого примем, что в отличие от метода ближайшего соседа допускаются небольшие отклонения в сторону увеличения расстояния Δi, не более некоторого числа ε. В итоге появляется несколько ближайших городов – список ψ_i, в котором |ψi| элементов. Список ψ_i упорядочен по увеличению расстояний δj входящих в него городов от gi, где δ_j ≤ Δ_i + ε, 1 ≤ j ≤ |ψ_i|. Становится возможным выбрать любой город из ψ_i, а не только один ближайший. Последовательностью будет список номеров M = {mi}, каждый из которых представляет собой порядковый номер элемента списка ψ_i, где 1 ≤ i < n.

В-третьих, необходимо не допускать слишком большого e, иначе ожидается, что метод станет неэффективным. В программной реализации, например, e уменьшается пропорционально снижению T.

В алгоритме используются следующие параметры, корректируемые пользователем в программе (табл. 1).

Таблица 1

Параметры алгоритма

* при которых достигнуто наилучшее решение из найденных для файла f1, см. ниже

Алгоритм следующий.

1. Вычислить среднее расстояние A между городами.

2. Чтение параметров, задаваемых пользователем.

3. Обнулить маршрут.

4. mi ← 1, где 1 ≤ i ≤ n (т.е. выбрать первые города из ψ_i). Найденный за все время минимум длины маршрута MIN ← 1000000.

5. Имитация отжига со стандартными параметрами – T = T0, число итераций и др.:

5.0. Увеличить максимальное число итераций. Номер итерации I ← 0.

5.1. I ← I +1. Изменение mi случайным образом (на ±1), причем вероятность изменения пропорциональна S, а вероятность увеличения обратно пропорциональна i, где 1 ≤ i ≤ E.

5.2. Считать g1 из введенных данных.

5.3. Нахождение следующего города для каждого города i, начиная с первого до предпоследнего:

5.3.1. Найти расстояние Δ до ближайшего города

5.3.2. Выбрать следующий город, пропуская mi – 1 более близких, при этом увеличение расстояния по сравнению с Δ не должно превышать ε = A×F×I /10, иначе выбирается город, пропуская mi – 2.

5.4. Подсчитать общую длину маршрута L.

Проверка условия имитации отжига для внесения изменений в M:

L ≤ MIN, либо L > MIN и:

random(P / (T0 – T)) > 6 и L – MIN < (P/(T0 – T)).

Если не выполнено, откат M на состояние до изменений.

5.5. Конец очередной итерации. Если не все итерации совершены, переход на 5.1.

5.6. Уменьшить T.

5.7. Если T ≥ 0, переход на 5.0;

6. Конец

Программа и исходные данные

Для реализации данного алгоритма разработана компьютерная программа в свободно распространяемой системе программирования Turbo Delphi 2006. Программа работает в операционной системе Windows, позволяет использовать подготовленные вручную исходные данные и генерировать их случайным образом. Число городов ограничено 40, но нетрудно перекомпилировать программу и для большего числа городов. Программа реализует также стандартный метод имитации отжига и метод ближайшего соседа.

В качестве исходных данных взяты широко известные наборы данных [6], специфические для задачи коммивояжера. В разных наборах [6] используется различный формат представления данных, и для каждого нужно разрабатывать собственную процедуру чтения входных данных. Поэтому использованы также наборы данных на основе входных файлов работы [1], которые представлены в ней в виде диаграммы. Эти файлы унифицированы по формату, и их легче использовать в программе. Кроме того, экспорт алгоритма в другую задачу облегчается экспортом тех же исходных данных.

В файлах [1] в качестве координат городов использованы характеристики объектов. Первая половина данных файла, ранее представлявшая значимости объектов ti, i=1,…n, теперь используются как набор значений по оси абсцисс (упрощенно, географические долготы городов). Вторая половина представляла длительности (ширины) pi, i=1,…n, теперь они применяются как значения по оси ординат (соответственно, географические широты). При открытии файла программа вычисляет евклидовы расстояния между каждой полученной точкой на плоскости. Эти расстояния принимаются за исходные данные для задачи коммивояжера. Координаты городов являются целочисленными, а расстояния между ними могут быть вещественными числами.

Результаты эксперимента

На рис. 1 представлена экранная форма, содержащая результаты работы нового алгоритма с данными файла f1 [1], которые приводятся в таблице 2.

Таблица 2

Данные файла f1

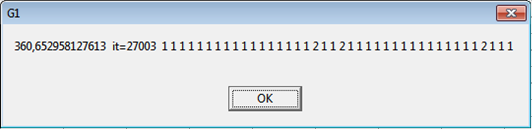
Рис. 1. Результат при использовании нового алгоритма для файла f1

— первое число (вещественное) – полученная длина маршрута;

— второе число – количество совершенных итераций;

— все остальные числа – последовательность M, специфичная для данного алгоритма.

На рисунке 2 приводится иллюстрация наилучшего из найденных новым алгоритмом маршрутов с данными файла f1.

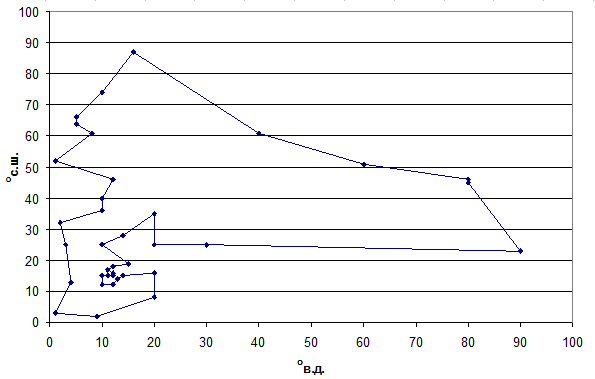
Рис. 2. Вид наилучшего из найденных маршрутов для файла f1

Города обозначены маркерами

Для обобщения результатов рассмотрена работа различных алгоритмов решения задачи коммивояжера с различными по статистическим характеристикам исходными данными (табл. 3).

Таблица 3

Результаты работы различных алгоритмов с различными исходными данными

Данные таблицы 2 позволяют сделать вывод, что из трех алгоритмов метод ближайшего соседа приводит к значительно менее оптимальным результатам, а новый алгоритм нередко позволяет получить наилучшие результаты.

Заключение

Недостатком нового алгоритма является низкая скорость вычислений. При использовании нового алгоритма скорость составляет около 7200 итераций в секунду, а при имитации отжига – около 350 000 итераций в секунду. Однако при сопоставлении этих двух методов иногда новый алгоритм достигает лучших результатов, и количество итераций для этого требуется меньше. Таким образом, адаптация алгоритма оптимизации последовательности отбора к решению задачи коммивояжера успешно проведена.

Рецензенты:

Соснин П.И., д.т.н., профессор кафедры вычислительной техники Ульяновского государственного технического университета, г. Ульяновск;

Макарычев П.П., д.т.н., профессор кафедры математического обеспечения и применения ЭВМ Пензенского государственного университета, г. Пенза.

Библиографическая ссылка