Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Данная работа предназначена для математического обоснования увеличения погрешности измерения окружности при уменьшении угла измеряемого сектора. На многих предприятиях  присутствуют детали, на которых задаются достаточно жесткие допуски на малых секторах окружности, опираясь на определенный парк измерительной техники предприятия. Вопросы повторяемости результатов (как одного из главных параметров при измерении и изготовлении) при таких измерениях возникают при использовании координатно-измерительных машин, которые рассчитывают погрешность, как указано на чертеже, как диаметр или радиус и граница допуска от них. Это не совсем правильный подход, с помощью геометрических вычислений ниже разберем причину таких расчетов. Также этот вариант вычисления предлагается, как один из методов теоретического определения величины погрешности измерения при уменьшении угла сектора и доказательства необходимости другого подхода к измерению таких поверхностей с помощью КИМ.

При вычислении центра окружности из секторасведем к определению окружности из трех точек– две по краям сектора и одну посередине сектора. Геометрическое вычисление центра в данном случае - пересечение перпендикуляров, выходящих из середин отрезков, соединяющих эти три точки. На рисунке 1 видно, как при малом угле сектора вырастает погрешность вычисления радиуса Sб и Sм от погрешности касания машины S – погрешность касания 2S, потому что погрешность машины +- S. β – полный угол сектора, l – длина участка, на котором расположен сектор – если сектор задан не углом, а радиусом и длиной участка[1; 2].

 

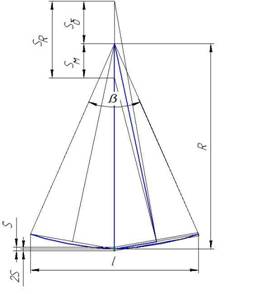
Рис.1.Погрешность вычисления радиуса:S – погрешность КИМ в точке измерения; R – радиус окружности, м; SR – погрешность радиуса окружности

Если сектор задан не углом, а радиусом и длиной участка l – то вычисление угла сектора показано на рисунке 2 (1).

 

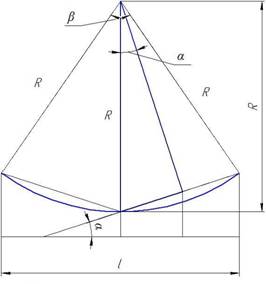
Рис.2. Вычисление угла сектора: β – полный угол раскрытия; α=β – четверть угла раскрытия (нужен для вычисления погрешности); l – длина участка, м;  R – радиус, м

Исходя из рисунка 2с помощью тригонометрических преобразований (1) выведем формулы для нахождения углов α и β (2):

 

 

 

 

(1)

 

(2)

Так как центральную точку изначально взяли посередине, то вычисление центра окружности сводится к пересечению одного из перпендикуляров (на рисунке 2 правого) отрезков с прямой, перпендикулярной отрезку, соединяющему две крайние точки, и проходящей через центральную точку. И дальнейшие вычисления будем проводить с этим прямоугольным треугольником[2-4].

На рис.3 выделяем этот треугольник для более подробного рассмотрения,S – погрешность машины, Sб – погрешность в большую сторону, Sм – погрешность в меньшую сторону, то же самое с углами.

 

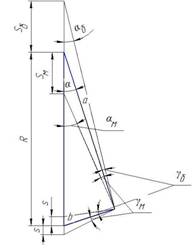
Рис.3.Вычисление погрешности с помощью прямоугольного треугольника

Расчет погрешности в меньшую сторону представлен на рис.4.

 

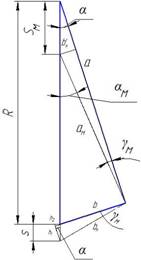
Рис.4. Расчет погрешности в меньшую сторону

Для того чтобы найти погрешность в меньшую сторону, необходимо использовать формулу (6), опираясь на расчеты (5). В формуле (6) неизвестным является угол погрешности (4), который можно вывести через вычисления (3) [4-5].

Дано:R, , S

 

 

(3)

(4)

 

 

 

 

 

(5)

 

(6)

 

Расчет погрешности в большую  сторону представлен на рис.5.

 

 

 

 

 

 

 

 

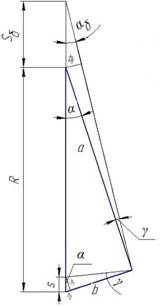
Рис.5. Расчет погрешности в большую сторону:R – радиус окружности, м; α – четверть угла раскрытия; S – погрешность измерения в точке; γ – угол погрешности

То же самое делаем для нахождения погрешности в большую сторону. Находим формулу для погрешности (8). В данном случае в формуле (8) неизвестной величиной является угол погрешности, который можно найти по формуле (7)[4-5].

Дано:R, α, S

 

 

 

 

(7)

 

 

 

 

(8)

 

Так как γ очень мал, то допустимо

 

 

 

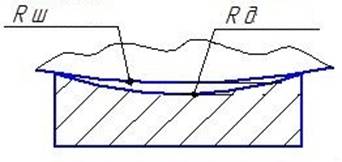
Рис.6.СравнениеR шаблона и R детали

Рис. 7. Отклонение от формы реального профиля. S-  отклонение от формы

На рисунке 6 показана методика измерения с помощью шаблона как одна из предполагаемых и в общем правильных методик измерения таких секторов, что R  детали совсем не равно R шаблона минус зазор, который определяется подбором щупа.R детали совсем другой, и его нужно вычислять – в данном случае такая методика измерения - это совсем не измерение радиуса или диаметра -этот зазор показывает отклонение от формы на данном участке (рис.7).  Напрашивается вывод, что именно отклонение от формы надо указывать в таких случаях, если бы не один подводный камень - отклонение от формы рассматривает ТОЛЬКО форму и не учитывает размер, то есть форма может быть хорошей, а размер совсем другим. В данном случае при использовании не шаблонов, а координатно-измерительных машин рекомендуется использовать - отклонение формы заданного профиля(не отклонение профиля продольного сечения – это совсем разные допуски) для окружности и отклонение формы заданной поверхности для измерения  сферической поверхности. Такая же методика используется при измерении криволинейных сечений, только тут номинальные точки находятся на секторе окружности.

Вывод

 В данной работе было проведено решение задачи по определению зависимости увеличения погрешности вычисления радиуса окружности от угла измеряемого сектора. Решение данной задачи показало, что чем меньшеугол измеряемого сектора, тем больше будет погрешность радиуса или диаметра окружности.

Рецензенты:

Беленький В.Я., д.т.н., проф., декан МТФ ПНИПУ, г. Пермь;

Сиротенко Л.Д,, д.т.н., проф.,  ПНИПУ, г. Пермь.