Обычно предлагаемые схемы оценки надежности оборудования основываются на представлении воздействия как случайного процесса, решении соответствующих задач статистической динамики для здания и оборудования, определении функции надежности (как вероятности пребывания параметров качества оборудования в допустимой области в течение заданного интервала времени) [3]. Однако практическая реализация такого (наиболее общего) подхода связана с определенными трудностями из-за недостаточной информации о статистических характеристиках воздействия, динамических характеристиках различного оборудования и т.п.
Между тем полезные оценки надежности оборудования (и его опорных конструкций) при статических и сейсмических воздействиях можно получить при расчетах по поэтажным спектрам в рамках квазистатического подхода.
Вектор сейсмических инерционных
нагрузок, отвечающих ![]() -й собственной форме
оборудования, равен:
-й собственной форме
оборудования, равен:
![]() (1)
(1)
где g – ускорение силы тяжести;
![]() –
поэтажный спектр (
–
поэтажный спектр (![]() и
и ![]() –
– ![]() -е собственная частота и затухание);
-е собственная частота и затухание);
![]() –
матрица масс;
–
матрица масс;
![]() –
соответствующим образом нормирования
–
соответствующим образом нормирования ![]() -я собственная форма.
-я собственная форма.
Вектор ![]() можно
рассматривать как случайный в силу неизбежного разброса величин
можно
рассматривать как случайный в силу неизбежного разброса величин ![]() ,
, ![]() и
и ![]() , связанного с вариацией интенсивности,
повторяемости и спектрального состава землетрясений, неточностью определения
характеристик сооружения и оборудования, условностью различных схем и т.п. По
вероятностным характеристикам величин, входящих в первую часть (1), могут быть
определены вероятностные характеристики
, связанного с вариацией интенсивности,
повторяемости и спектрального состава землетрясений, неточностью определения
характеристик сооружения и оборудования, условностью различных схем и т.п. По
вероятностным характеристикам величин, входящих в первую часть (1), могут быть
определены вероятностные характеристики ![]() , а
затем вероятность превышения заданных предельных величин (напряжений, смещений
и т.д.), от которых зависят прочность и работоспособность оборудования. Задача
решается в следующем порядке: определение на основе имеющейся информации
вероятностных характеристик параметров воздействия, сооружения и оборудования
(математических ожиданий, дисперсий, функций распределения и т.п.); построение
ПА и ПС с учетом вариации расчетных схем, деформационных характеристик и
параметров затухания сооружения и оборудования; определение вероятностных
характеристик
, а
затем вероятность превышения заданных предельных величин (напряжений, смещений
и т.д.), от которых зависят прочность и работоспособность оборудования. Задача
решается в следующем порядке: определение на основе имеющейся информации
вероятностных характеристик параметров воздействия, сооружения и оборудования
(математических ожиданий, дисперсий, функций распределения и т.п.); построение
ПА и ПС с учетом вариации расчетных схем, деформационных характеристик и
параметров затухания сооружения и оборудования; определение вероятностных
характеристик ![]() и
и ![]() ;
статический расчет оборудования (и опорных конструкций) на случайную нагрузку
;
статический расчет оборудования (и опорных конструкций) на случайную нагрузку ![]() и определение усилий
и определение усилий ![]() (или напряжений) по каждой собственной
форме; определение вероятностных характеристик расчетных усилий
(или напряжений) по каждой собственной
форме; определение вероятностных характеристик расчетных усилий 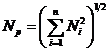 (
(![]() —
число учитываемых форм); оценка надежности оборудования при особом сочетании воздействий
(т.е. при статических и сейсмических нагрузках) и принятом критерии отказа.
—
число учитываемых форм); оценка надежности оборудования при особом сочетании воздействий
(т.е. при статических и сейсмических нагрузках) и принятом критерии отказа.
В данной работе в первом приближении принимается следующая система основных допущений: повторяемость землетрясений подчиняется закону Пуассона; величина пикового ускорения (в пределах данного балла) распределена по нормальному закону, при построении ПА используются линейно-упругие расчетные модели сооружений.
В силу последнего допущения
![]() (2)
(2)
где ![]() –
пиковое значение ускорения грунта;
–
пиковое значение ускорения грунта;
![]() –
спектр при
–
спектр при ![]() ;
;
![]() –
параметры расчетной модели (жесткость основания, характеристики затухания и
т.д.), рассматриваемые как случайные величины.
–
параметры расчетной модели (жесткость основания, характеристики затухания и
т.д.), рассматриваемые как случайные величины.
Далее можно принять, что величины ![]() для каждого
для каждого ![]() вычисленные
по акселерограммам различного спектрального состава и длительности при
вариациях
вычисленные
по акселерограммам различного спектрального состава и длительности при
вариациях ![]() , распределены по нормальному закону. В
другом варианте можно принять, что по нормальному закону распределены параметры
, распределены по нормальному закону. В
другом варианте можно принять, что по нормальному закону распределены параметры
![]() . При этом, как обычно в задачах такого
типа, гипотеза нормальности, принимаемая непосредственно относительно величин
. При этом, как обычно в задачах такого
типа, гипотеза нормальности, принимаемая непосредственно относительно величин ![]() либо относительно параметров расчетной
модели
либо относительно параметров расчетной
модели ![]() , а также для величин пиковых ускорений,
прочностных характеристик и иного, рассматривается в качестве первого
приближения, восполняющего недостаток эмпирических данных о реальных распределениях.
, а также для величин пиковых ускорений,
прочностных характеристик и иного, рассматривается в качестве первого
приближения, восполняющего недостаток эмпирических данных о реальных распределениях.
При использовании второго подхода
функцию ![]() можно линеаризовать по параметрам
можно линеаризовать по параметрам ![]() при фиксированном значении
при фиксированном значении ![]() :
:
![]() (3)
(3)
где ![]() ,
, ![]() – соответствующие коэффициенты. Тогда
величины
– соответствующие коэффициенты. Тогда
величины ![]() также будут распределены по нормальному
закону с математическим ожиданием и дисперсией:
также будут распределены по нормальному
закону с математическим ожиданием и дисперсией:
![]() ;
;
![]() (4)
(4)
где ![]() ;
; ![]() — корреляционная матрица параметров
— корреляционная матрица параметров ![]() .
.
Коэффициент корреляции между ![]() и
и ![]()
![]() (5)
(5)
В частном случае, когда параметры ![]() некоррелированы,
некоррелированы,
![]() ;
;
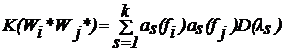 . (6)
. (6)
Разложив правую часть (2) в ряд Тейлора в окрестности точки
(m(A), m(W*)), получим в линейном приближении:
![]() (7)
(7)
т.е. величины ![]() так
же будут распределены по нормальному закону с математическим ожиданием и
дисперсией:
так
же будут распределены по нормальному закону с математическим ожиданием и
дисперсией:
![]()
![]() (8)
(8)
Коэффициент корреляции между ![]() и
и ![]() равен
равен
![]() (9)
(9)
Усилия (напряжения) в оборудовании ![]() , соответствующие сейсмическим нагрузкам
по
, соответствующие сейсмическим нагрузкам
по ![]() -й форме, определяются линейной
комбинацией компонент
-й форме, определяются линейной
комбинацией компонент ![]() , т.е.
, т.е.
![]() (10)
(10)
где ![]() ;
; ![]() — соответствующие коэффициенты.
— соответствующие коэффициенты.
Таким образом, ![]() распределены по нормальному закону с
математическим ожиданием и дисперсией:
распределены по нормальному закону с
математическим ожиданием и дисперсией:
![]()
![]() (11).
(11).
Коэффициент корреляции между усилиями по двум различным формам:
![]() (12)
(12)
Из формулы для расчетных усилий 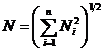 в линейном приближении получаем:
в линейном приближении получаем:
![]() (13)
(13)
т.е. N также распределено по нормальному закону с математическим ожиданием и дисперсией:
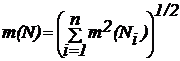 (14)
(14)
где ![]()
![]() — корреляционная матрица усилий Ns.
— корреляционная матрица усилий Ns.
Если при расчете оборудования учитываются несколько различных сейсмических усилий, например N(1) и N(2) , то их математические ожидания и дисперсия вычисляются по формулам (14), а коэффициент корреляции между N(1) и N(2)
![]()
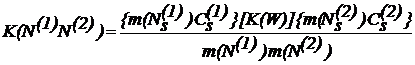 (15)
(15)
где ![]() ;[K(N)] — корреляционная матрица значений Ws.
;[K(N)] — корреляционная матрица значений Ws.
Критерий прочности (жесткости, устойчивости и т.п.) или работоспособности оборудования
F(G, R)≥0, (16)
где F – заданная функция параметров нагрузки (в том числе сейсмической) G и прочности R. Во многих случаях он может быть сведен к виду:
F=R-G≥0, (17)
где F имеет смысл резерва прочности [4]. В этом случае вероятность отказа
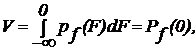 (18)
(18)
где pf и Pf — плотность и интегральный закон распределения F соответственно.
Если F распределена по нормальному закону, то
V=0.5-Ф(γ), (19)
где 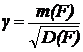 , а Ф
– интеграл вероятности Гаусса.
, а Ф
– интеграл вероятности Гаусса.
При больших значениях γ используется асимптотическая формула [4]
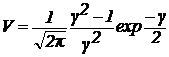 (20)
(20)
Если оборудование, срок службы
которого T, работает в r
различных режимах продолжительностью ti
каждый ![]() , при которых оно имеет различные
динамические характеристики (собственные частоты, формы и т.п.), то вероятность
отказа может быть определена по формуле полной вероятности:
, при которых оно имеет различные
динамические характеристики (собственные частоты, формы и т.п.), то вероятность
отказа может быть определена по формуле полной вероятности:
![]() (21)
(21)
где Vi – вероятность отказа при i-м режиме работы, определяемая по формуле (18).
Аналогично учитываются направления
сейсмического воздействия, а также повторяемость землетрясений разной
интенсивности (например, ПЗ и МРЗ, фигурирующих в нормативных расчетах). Так,
если вероятность ![]() землетрясения с периодом
повторяемости
землетрясения с периодом
повторяемости ![]() за срок службы оборудования
за срок службы оборудования ![]() равна и задано m акселерограмм, то полная вероятность отказа оборудования
может быть оценена снизу и сверху с помощью соотношений:
равна и задано m акселерограмм, то полная вероятность отказа оборудования
может быть оценена снизу и сверху с помощью соотношений:
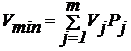 (22)
(22)
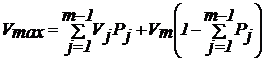 (23)
(23)
где ![]() —
вероятность отказа при j-м землетрясении,
в качестве
—
вероятность отказа при j-м землетрясении,
в качестве ![]() в (23) следует принять наименьшую из
вероятностей отказа.
в (23) следует принять наименьшую из
вероятностей отказа.
Обычно при ПЗ и МРЗ предъявляются различные требования к оборудованию, что может быть учтено путем использования разных критериев отказа.
В качестве примера дается оценка надежности опорной конструкции цилиндрического резервуара с жидкостью (водой), установленного на трех стойках, жестко закрепленных в корпусе и шарнирно опертых на основание (рис. 1).
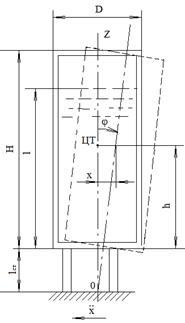
Рис. 1. Резервуар с жидкостью
Сооружение, в котором установлен резервуар, может подвергаться землетрясениям с интенсивностью I1 = 8 баллов (с периодом повторяемости T1 = 10 000 лет), I2 = 7 баллов (T2 = 100 лет) и I3 = 6 баллов (Tз<100 лет). В таблице 1 приводятся величины m(A) и D(A), вычисленные на основе интегральных законов распределения [5], а также вероятности Pj землетрясений за срок службы резервуара 30 лет (вероятность шестибалльного землетрясения принята P3 = 1 – (P1+P2)).
таблица 1
|
Вероятностные характеристики землетрясений |
|||||
|
Номер Землетря- сения, i |
Интенсив-ность Ii, , балл |
Период пов- по торяемости, Тi, лет |
Пиковое ускорение, А (g) |
Вероятность за срок службы, Рi |
|
|
Математическое ожидание, m(A) |
Дисперсия, D(A) |
||||
|
1 2 3 |
8 7 6 |
10000 100 100 |
0,2 0,1 0,05 |
4,4∙10-3 1,1∙10-3 2,8∙10-4 |
0,003 0,222 0,775 |
Случайными параметрами расчетной модели являются: λ1 – модуль упругости грунтового основания, на котором расположено сооружение (E·10-4 МПа); λ2 – затухание в оборудовании (в процентах от критического). Коэффициенты линеаризации спектра W* (f, λ1, λ2) определяются по формуле (3), выполняемой методом наименьших квадратов (для простоты примера спектр принят одинаковым при всех землетрясениях).
Расчетная схема резервуара представляет собой твердое тело с двумя степенями свободы (x и φ); масса жидкости суммируется с собственной массой резервуара [1]; резервуар работает в двух режимах (t1 – время заполнения до верха, а t2 – на высоту l); воздействие приложено горизонтально, в плоскости чертежа, оба направления равновероятны.
Критерий отказа одной стойки – развитие напряжений, превышающих временное сопротивление σвр (также распределенное по нормальному закону); критерий отказа опорной конструкции – выход из строя хотя бы одной стойки.
Критерий прочности для стоек, расположенных слева и справа от оси OZ (при показанном на рисунке 1 направлении воздействия Х0), имеет вид:
Fл= σвр – σс + σс.в ≥ 0;
Fп= σвр – σс – σс.в ≥ 0,
где σс и σс.в – напряжения от сейсмики и собственного веса соответственно. При перемене направления воздействия условия (25) и (26) меняются местами.
Расчеты выполнялись при следующих исходных данных: диаметр резервуара D = 150 см; высота Н = 450 см; длина стойки lст = 100 см, площадь ее поперечного сечения Fст = 18,8 см2, момент инерции I ст=340 см4,
момент сопротивления Wст = 54,4 см3; масса сухого резервуара Q = 3,8 т, центральный момент инерции относительно горизонтальный оси lp = 10 т-м2 ; срок службы резервуара 30 лет; общее время работы при заполнении до верха t1 = 6 лет; время работы при заполнении на высоту l = 1,7 м t2 = 24 года; математические ожидания и дисперсии случайных параметров и прочностных характеристик: m (λ1) = 1,06 * 10-2 МПа; D (λ1) = 0,26 * 10-4 МПа2; m (λ2) = 3; D (λ2) = 0,33; m (σвр.) = 718 МПа; D (σвр.) = 5155 МПа2; σс.в. = 20,7 МПа.
При интенсивности I1 = 8 баллов в случае полного резервуара вероятность отказа оказывается равной: для левой стойки V’л = 0,79, для правой стойки V’п = 0,81, для опорной конструкции в целом V’l = 0,992 (надежность ψ = 8 * 10-3).
При частичном заполнении резервуара вероятность отказа опорной конструкции V’l = 9 * 10-12. Полная вероятность отказа при 8 баллах V’l = 0,198, при 7 и 6 баллах соответственно V2 = 0,094 и V3 = 9,06 * 10-5. В результате вероятности отказа опорной конструкции оказывается равной V = 0,021, т. е. надежность ψ = 1– V = 0,979.
Таким образом, надежность конструкции оказывается достаточно высокой, хотя при l1 = 8 баллов и заполненном резервуаре математическое ожидание сейсмических напряжений на 75% превышает значение σвр, данное в сортаменте, и при обычном расчете опорная конструкция была бы признана несейсмостойкой.
Надежность может быть повышена за счет несложных конструктивных мероприятий. Так, если установить резервуар на шести стойках вместо трех (при той же суммарной площади их сечения, т.е. металлоемкости конструкции), то можно принять за критерий отказа выход из строя трех рядом расположенных стоек или более трех стоек. В этом случае вероятность отказа составляет V = 1,85*10-3, т.е. уменьшается более чем в 10 раз.
Рецензенты:Кравец С.Б., д.т.н., профессор, зав. отделом сейсмостойкости ВНИИАМ, г. Волгодонск;
Созаев В.А., д.ф.-м.н., профессор, зав. кафедрой общей физики ГМИ, г. Владикавказ, профессор кафедры физики наносистем КБГУ, г. Нальчик.
Библиографическая ссылка
Суюмбаев Х.У., Ногеров И.А., Шогенов Б.В., Макшаева М.И. ОЦЕНКА НАДЕЖНОСТИ ОБОРУДОВАНИЯ АЭС В РАМКАХ ЛИНЕЙНО-СПЕКТРАЛЬНОЙ ТЕОРИИ СЕЙСМОСТОЙКОСТИ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=20548 (дата обращения: 24.01.2026).



