Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

                                                                  (1)

                                                                                                                               (2)                                                                                                                                                                                                                                         (3)

где   - фиксированная точка интервала ,  и  - положительные числа. Коэффициент в уравнении (1) предполагается отличным от нуля хотя бы в одной точке отрезка . 

Пусть   и  - решения дифференциальных задач

                                            (4)

,                                                           (5)

соответственно. Приведём формулировки теорем, в которых даются необходимые и достаточные условия однозначной разрешимости задачи (1)-(3).

Теорема 1. Пусть  ,   и  выполнено условие       

.                                                                                                                                                   (6)

Тогда задача  (1)-(3) однозначно разрешима в  классе  , и её решение представимо

в виде       

.                                                                                                            (7)

Теорема 2. Пусть  ,   и функция   такова, что для всех    выполнено условие

.                                                                                                                                (8)

Тогда решение задачи (1)-(3) существует, единственно и принадлежит классу .

Эти теоремы доказаны в работах , . В дальнейшем будем считать, что выполнены условия В: ,  .           

Имеет место

Теорема 3. Если удовлетворяют условию В и выполнено   (8), то решение задачи (1)-(3) принадлежит классу .

Доказательство этой теоремы следует из однозначной разрешимости задач (4) и (5) в классе  при выполнении условий В, и представления решения в виде (7).

Введём  на отрезке  равномерную сетку  . Шаг  сетки   выберем  меньше половины меньшего из отрезков .  Номер    выберем из  условия  .  Используем для сеточной функции , определённой на , обозначение :.  Дифференциальную задачу (4) аппроксимируем конечно-разностной схемой

,                                                                         (9)

,

,

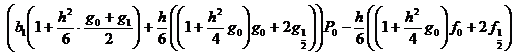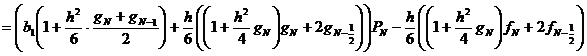где      ,   

а дифференциальную задачу (5) - конечно-разностной схемой

          ,                                                               (10)

,

,

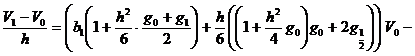
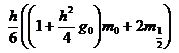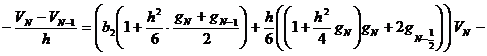
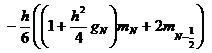где .

Конечно-разностные схемы (9) и (10) аппроксимируют задачи (4) и (5) соответственно, с точностью  , что не трудно показать с помощью разложений по формуле Тейлора.

Пусть

,                                                      (11)

полином Лагранжа третьей степени, проведённый через точки,,, .  Коэффициенты  Лагранжа вычисляются по формулам:

 ,   ,

,   .                                 (12)

Введём обозначение   и покажем, что    аппроксимирует значение  с точностью . В силу равенств  , и ограниченности коэффициентов Лагранжа,  . Поскольку полином  аппроксимирует функцию  на отрезке  с точностью , что следует из известной оценки погрешности полинома Лагранжа , то найдётся положительная постоянная , не зависящая от  , что

.                                                                                                          (13)

Аналогично,  аппроксимируются величиной  с точностью  , следовательно,  найдётся постоянная , что

.                                                                                                                      (14)

В качестве приближённого решения задачи (1)-(3) выберем сеточную функцию :

, .                                                                                           (15)

Имеет место

Теорема  4. Пусть  выполнены условия В и (8).  Тогда сеточная функция ,  определённая по формуле (15), сходится при    к  решению  задачи (1)-(3) со скоростью    в равномерной метрике.

Доказательство. Используя представление (7) решения задачи (1)-(3),  получим оценку погрешности    в равномерной метрике:

.                                                                                       (16)

Оценим слагаемые в правой части (16). Сначала оценим . Отметим, что в силу принципа максимума разностной краевой задачи третьего  рода , решения задачи (10) положительны. Перепишем уравнение (10) в виде                                                   

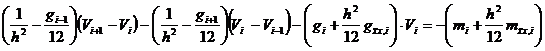.    (17)

Пусть положительный максимум   функции достигается в точке , т.е.  , где . Тогда,  в силу ,  ,  из  (17)  получаем оценку

.                                                                                         
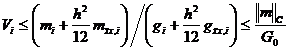Если , то из левого краевого условия (10) следует оценка:

.       

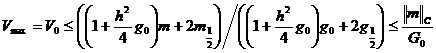Если , то из правого краевого условия (10) следует оценка:

         .                    

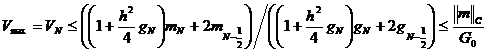Таким образом, для решения задачи  (10)  имеет место оценка:

.                                                                                                                        (18)

С  учётом аппроксимации порядка   разностной схемы (10) на решении задачи (4), найдётся положительная постоянная  , что                                                                            .                                                                                                          (19)

Также найдется положительная постоянная ,что

.                                                                                                                      (20)

Введём обозначение  .  Если выполнено условие (8), то, как следует  из       принципа максимума  третьей краевой задачи  для оператора Штурма-Лиувилля , , при этом имеет место оценка

 .                                                                                                                                (21)

Получим нижнюю оценку выражения .  Пусть - шаг сетки, что . Тогда при  оценка  (13) принимает вид  , откуда следует:

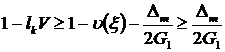.                                                                                    (22)

Применяя оценки (13), (14), (18)-(22) из (16) получаем:

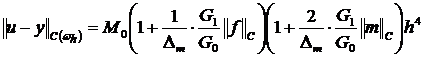.                                              (23)

Из оценки (23) следует утверждение теоремы 4.

Рецензенты:  

Шхануков-Лафишев М.Х. д.ф.-м.н., профессор, ФГБУН Институт информатики и проблем регионального управления   Кабардино-Балкарского научного центра РАН, г. Нальчик;

Ашабоков Б.А,, д.ф.-м.н., профессор, Высокогорный  Геофизический  Институт, г. Нальчик.