Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Среди основных направлений инновационной модернизации современного высшего заочного образования выделяются внедрение электронных форм обучения [2-5; 7; 9], автоматизация контроля динамики результата обучения и знаний студентов с применением дистанционных образовательных технологий [3; 6-8]. В связи с этим представляет интерес статистический анализ качества образовательного процесса в вузе.

В данной работе аналогично [1] проведен статистический анализ в пакете Statistica результатов оценивания знаний по высшей математике в объеме первых трех семестров студентов института электронного обучения (выборка ЭО) Томского политехнического университета. Рассмотрение проведено в системе 2 показателей: ЭКЗ – результат тест-экзамена в режиме online (по 5-балльной шкале) и DT – разность моментов окончания и начала экзамена (в минутах). Гистограммная динамика результатов ЭКЗ по семестрам отражена на рис. 1.

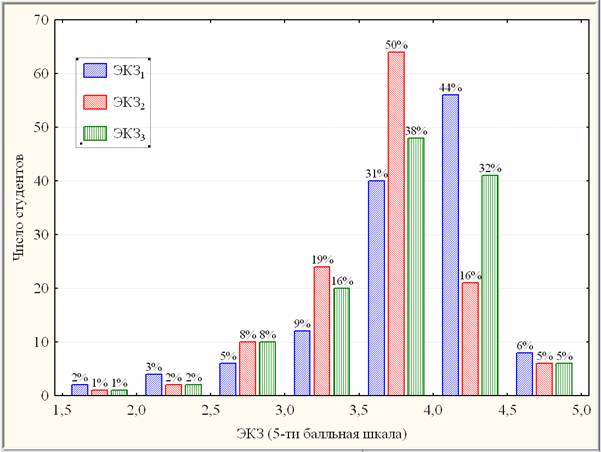
Рис. 1. Составная гистограмма ЭКЗ.

Согласно рис. 1, интервал двоечников [0; 2,5) является малочисленным (3-5%). В интервале слабых троечников [2,5; 3) сначала наблюдается рост результатов экзаменационной (ЭКЗ) успеваемости в 1,6 раза (с 5% в 1-м семестре до 8% во 2-м семестре), а затем стабильный уровень (8%). В интервале сильных троечников [3; 4,5) результаты ЭКЗ сначала выросли в »2,1 раза (с 9% в 1-м семестре до 19% во 2-м семестре), а затем уменьшились в »1,2 раза (до 16% в 3-м семестре). Наиболее представительным является интервал слабых хорошистов [3,5; 4). Здесь результаты ЭКЗ сначала выросли в »1,61 раза (с 31% в 1-м семестре до 50% во 2-м семестре), а затем уменьшились в »1,32 раза (до 38% в 3-м семестре). В интервале сильных хорошистов [4; 4,5] результаты экзаменационной успеваемости, наоборот, сначала уменьшились в 2,75 раза (с 44% в 1-м семестре до 16% во 2-м семестре), а затем выросли в 2 раза (до 32% в 3-м семестре). В интервале отличников [4,5; 5] ЭКЗ стабильны на уровне 5-6%. 

Гистограммная динамика результатов DT по семестрам отражена на рис. 2.

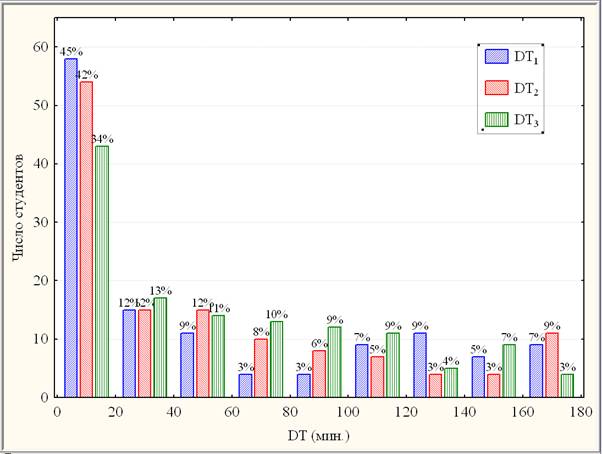
Рис. 2. Составная гистограмма DT

Согласно рис. 2, доля положительно сдавших тест-ЭКЗ  за DT < 20 минут из выделенных 3 часов превышает ⅓. Среди сдавших ЭКЗ1 был установлен троекратно рекорд минимального DT1, = 4 мин, побитый троекратно во 2-м семестре минимальным DT2, = 3 мин. Заметим, что доля «легкодумов» (DT < 20) имеет отрицательную динамику и сократилась в »1,3 раза (с 45% в 1-м семестре до 34% в 3-м семестре).

Выявленное аномальное обстоятельство лишний раз подчеркивает несовершенство стадии оценивания усвоенных студентом знаний при дистанционном обучении с использованием ДОТ, создающее проблему идентификации студента [1; 10].

В связи с тем что согласно теории измерительных шкал балльная шкала измерения ЭКЗ относится к типу порядковых шкал, а распределение DT даже визуально (рис. 2) не похоже на нормальное, для сравнения рассматриваемых выборок предлагается использовать прежде всего ранговые (непараметрические) критерии.

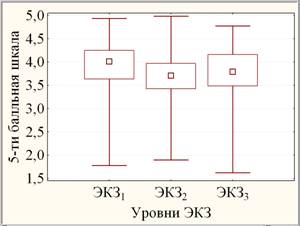
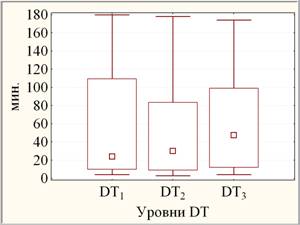
Согласно ранговому дисперсионному анализу Фридмана с повторными измерениями динамика ЭКЗ, то есть различия между результатами ЭКЗ1, ЭКЗ2 и ЭКЗ3 по их совокупности, оценивается как высоко значимая (на уровне значимости р < 0,0005) за счет  высоко значимого отличия ЭКЗ1 от ЭКЗ2 (р »0,00003< 0,0005), статистически значимого отличия ЭКЗ2 от ЭКЗ3 (0,005<р »0,023< 0,050) при незначимом различии между ЭКЗ1 и ЭКЗ3 (0,10<р). В случае DT выделено только статистически значимое различие между DT2 от DT3 (0,005<р »0,032< 0,050). Графические числовые непараметрические характеристики ЭКЗ  и DT представлены на рис. 3 (слева и справа соответственно).

Рис. 3. Медианные диаграммы размаха ЭКЗ и DT («квадрат» - медианы; ящик - квартильный размах (25%-75%); усы – полный размах)

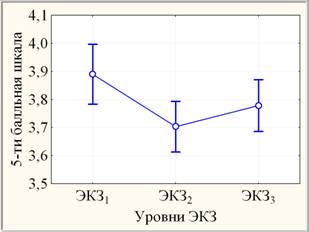
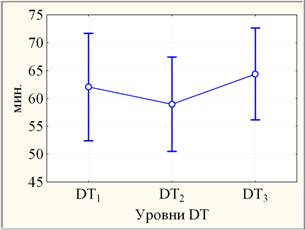
По параметрическому дисперсионному анализу с повторными измерениями динамика ЭКЗ (рис. 4, слева) оценивается как статистически значимая (0,005<р »0,015< 0,050) по совокупности трех семестров за счет отличия ЭКЗ2 от ЭКЗ1 – сильно значимо (0,0005< р »0,001< 0,005), от ЭКЗ3 – слабо значимо (0,05<р»0,09< 0,10) при незначимом (р »0,13> 0,1) различии между ЭКЗ3 и ЭКЗ1. В случае DT различия по семестрам оцениваются как незначимые. Графические числовые параметрические характеристики ЭКЗ  и DT представлены на рис. 4 (слева и справа соответственно).

Рис. 4. Линейные графики средних с  95%-ными границами доверительных интервалов

(слева - ЭКЗ, справа - DT)

С другой стороны, в рамках однофакторного дисперсионного анализа независимых выборок с помощью непараметрического критерия Краскела-Уоллиса можно оценить различия между экзаменационными результатами разных 7 групп как незначимые (р > 0,1) в случае ЭКЗ1 и ЭКЗ3, а в случае ЭКЗ2 как статистически значимые (0,005 < р »0,018 < 0,05) за счет отличия Б12 от Г2 – статистически значимого (0,005 < р »0,02 < 0,05) и от А3 – слабо значимого (0,05 < р »0,06 < 0,1). Различия результатов DT по семестрам оцениваются в случае DT1 как сильно значимые (0,0005 < р »0,0006  < 0,005) за счет сильно значимых отличий Г1 от А1 и Б12, статистически значимого различия между А1 и А3 (0,005 < р »0,034 < 0,05) и слабо значимого различия между Б12 и А3 (0,05 < р »0,06 < 0,10); в случае DT2 как высоко значимые ( р < 0,0005) за счет сильно (0,0005 < р < 0,005)  значимого отличия А1 от А3, Г1, Г2 и Г3, а также слабо (0,05 < р < 0,10) значимого отличия Б12 от А3 и Г2; в случае DT3 как высоко значимые ( р < 0,0005) за счет отличия А1 от Г1 – сильно значимо и Г3 – статистически значимо, а также отличия Б12 от Г1 – высоко (р < 0,0005) значимо, от Г3 – сильно (р »0,003)  значимо, от Г2 – статистически (р »0,03) значимо и от А3 – слабо (р »0,07) значимо.

По параметрическому дисперсионному анализу независимых выборок с помощью F- критерия можно оценить различия между экзаменационными результаты разных 7 групп как незначимые (р > 0,10) в случае ЭКЗ1 и ЭКЗ3, а в случае ЭКЗ2 как слабо значимые (0,05 < р »0,06 < 0,010) за счет отличия Б12 от Г2 – статистически значимого (0,005 < р »0,034 < 0,050) и от А3 – слабо значимого (0,05 < р »0,06 < 0,10). В случае DT различия по семестрам оцениваются как высоко значимые (р »0,0003 < 0,0005): в случае DT1 за счет сильно значимых (0,0005 < р < 0,0050)  отличий А1 от А3, Г1, Г2 и Г3, а Б12 от А3, Г1, Г2 и Г3; в случае DT2 за счет высоко значимых (р < 0,0005)  отличий А1 от А3, Г1, Г2 и Г3,  сильно значимых (0,0005 < р < 0,0050)  отличий А2 от Г1, Г2 и Г3, а Б12 от Г1, Г2 и Г3, статистически значимых (0,005 < р < 0,050) отличий А3 от А2 и Б12; в случае DT3 за счет отличий А1 от Г1 – высоко значимого, от Г3 – сильно значимого, от А3 и Г2  – статистически значимых, а также отличий Б12 от Г1, Г2 и Г3 – высоко значимых, от А2 и А3 – сильно значимых.

На основании параметрического дисперсионного анализа повторных измерений (семестровая динамика ЭКЗ и DT) и независимых выборок (однородность ЭКЗ и DT по группам) можно оценить значимость динамики учебных групп в координатах DT и ЭКЗ (рис. 5).

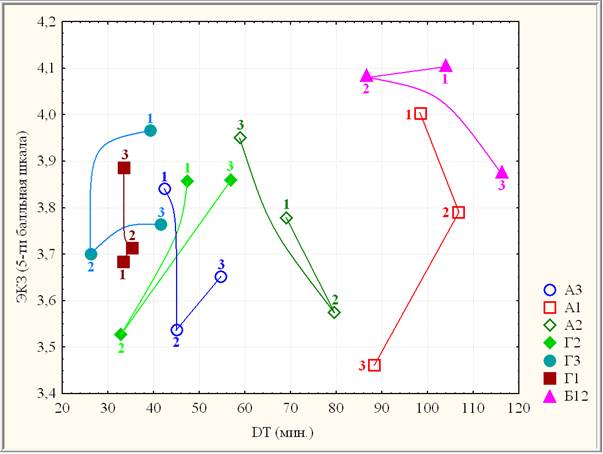
Рис. 5. Динамическая диаграмма рассеяния учебных групп в координатах DT и ЭКЗ

Можно провести классификацию составной (по ЭКЗ и DT) динамики учебных групп по уровню ее значимости в порядке возрастания:

Г1 имеет незначимую (на уровне  р > 0,10) динамику ЭКЗ и DT;

Г3 и А3 имеют слабо значимую динамику ЭКЗ за счет отличия ЭКЗ2 от ЭКЗ1  (0,05 < р < 0,10) при незначимой динамике DT;

Б12 имеет незначимую динамику ЭКЗ и статистически значимую динамику DT за счет отличия DT2 от DT3 (0,005 < р » 0,026 < 0,050);

А2 имеет статистически значимую динамику ЭКЗ за счет отличия ЭКЗ2 от ЭКЗ3 (0,005 < р » 0,040 < 0,050)  и слабо значимую динамику DT за счет отличия DT2 от DT3 (0,05 < р » 0,07 < 0,10);

А1 имеет сильно значимую динамику ЭКЗ за счет отличия ЭКЗ1 от ЭКЗ3 (0,0005 < р » 0,002 < 0,005)  и слабо значимую динамику DT за счет отличия DT2 от DT3 (0,05 < р » 0,09 < 0,10);

Г2 имеет статистически значимую динамику ЭКЗ за счет отличия ЭКЗ2 от ЭКЗ1 и ЭКЗ3 (0,005 < р » 0,02 < 0,05)  и статистически значимую динамику DT за счет отличия DT2 от DT3 (0,005 < р » 0,007 < 0,050);

Наличие массового кластера «успешных легкодумов» {Г1, Г2, Г3, А3} свидетельствует об обострении проблемы идентификации оцениваемого студента [1; 10].

Еще одной острой проблемой оценивания усвоенных студентом-заочником знаний в режиме ДОТ продолжает оставаться чрезмерное увлечение автоматизацией (практически без участия преподавателя) итогового контроля знаний обучаемых в условиях несовершенства содержания и формы тестовых заданий, что приводит к завышению на целый балл (по 5-балльной шкале) результатов оценивания усвоенных студентом-заочником знаний в режиме ДОТ по сравнению с классическим режимом [1].

Результаты проведенного анализа оценивания знаний студентов-заочников в режиме ДОТ могут быть учтены при внедрении современных информационных образовательных интернет-технологий в организацию электронного обучения для обеспечения качества образования и контроля знаний.

Выводы

1.    Проведена гистограммная динамика результатов ЭКЗ и DT электронного обучения по высшей математике в объеме первых трех семестров.

2.    Согласно ранговому дисперсионному анализу Фридмана с повторными измерениями динамика ЭКЗ оценивается как высоко значимая по совокупности трех семестров за счет высоко значимого отличия ЭКЗ1 от ЭКЗ2, статистически значимого отличия ЭКЗ2 от ЭКЗ3  при незначимом различии между ЭКЗ1 и ЭКЗ3. В случае DT выделено только статистически значимое различие между DT2 от DT3. Данные результаты подтверждены параметрическим дисперсионным анализом с повторными измерениями в более мягкой форме.

3.    С помощью непараметрического критерия Краскела-Уоллиса все выборки семестровых результатов ЭКЗ и DT оценены на групповую неоднородность (различия между результатами разных 7 групп): в случае ЭКЗ1 и ЭКЗ3 – как незначимые, ЭКЗ2  – статистически значимые, DT1 – сильно значимые, DT2 и DT3 – высоко значимые. Данные результаты подтверждены параметрическим дисперсионным анализом.

4.    На основании параметрического дисперсионного анализа повторных измерений и независимых выборок проведена классификация составной (по ЭКЗ и DT) динамики учебных групп по уровню ее значимости.

 

Работа выполнена при поддержке Российского научного фонда.

Рецензенты:

Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск;

Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет, г. Томск.