Историю изучения вихревых движений жидкости можно отсчитывать с основополагающей работы Гельмгольца (Helmholtz, 1858) «Об интегралах гидродинамических уравнений, соответствующих вихревым движениям» [4]. Затем они проводились Лордом Кельвином [5], а также Прандтлем и его Геттингенской школой в первой половине прошлого века [6]. В последние три десятилетия параллельно с развитием науки стали появляться многочисленные прикладные технические и технологические проблемы, такие как проблемы устойчивости и контроля течений, аэродинамики треугольного крыла, летательных аппаратов с большой подъемной силой, опасности, связанные со струйными следами крупных летательных аппаратов, и т.д. [5].
В огромном многообразии вихревых движений повышенный интерес вызывают концентрированные вихри с точки зрения как фундаментальных исследований, так и практики. Достаточно четкое определение концентрированного вихря (рис. 1) можно дать для случая идеальной жидкости: это локализованная в пространстве область с ненулевой завихренностью, окруженная потенциальным течением.
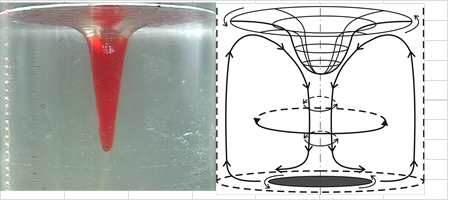
Рис. 1. Концентрированный вихрь [3]
В случае идеальной жидкости характерной особенностью концентрированного вихря является локализация завихренности в области пространства цилиндрической формы, внутри которой среда вращается практически как твердое тело, а вне этой области вращательное движение быстро спадает с удалением от центра до нулевого значения.
В настоящее время актуальной проблемой является описание перемещения в концентрированном вихре какого-либо объекта. Поскольку плавучий объект обладает присущими ему физико-химическими характеристиками, отличающимися от характеристик жидкой среды, при описании его движения необходимо вводить поправки, учитывающие взаимодействие среды с объектом. Применительно к геофизике такие поправки могут оказаться полезными, например, при исследованиях, связанных с проблемой накопления пластикового мусора в центрах вихревых образований в открытом океане, а также для корректировки показаний различных зондов-дрифтеров, передающих информацию о морских и океанских течениях.
Целью данной работы являлось выявление закономерностей в перемещении твердотельных и жидких маркеров по поверхности вращающейся жидкости в условиях воспроизводимых внешних параметров.
Описание эксперимента. Опыты выполнены на стенде моделирования «Вихревые течения с кручением», входящим в комплекс уникальных установок «Гидрофизический комплекс ИПМех РАН». Вихревое течение создавалось вращающимся диском, установленным на дне прозрачного цилиндрического контейнера, который приводился во вращение установленным снизу электромотором. Бассейн заполняется водой, уровень жидкости задавался отдельно для каждой серии экспериментов. В качестве несмешивающейся примеси использовалось рафинированное подсолнечное масло, в качестве твердотельных маркеров — полипропиленовые объекты в форме квадрата со стороной 2 см, звезды размером 1,5 см, пробирки высотой 3 см, а также квадрата со стороной 1 см, покрытые растворимой краской (рис. 3, а). Варьирование глубины слоя жидкости, размеров и частоты вращения диска позволяет изучать воспроизводимую картину вихревого течения в широком диапазоне параметров. Более подробное описание установки приведено в [3].
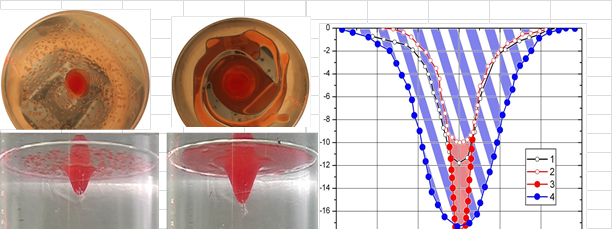
Результаты исследования. Опыты последних лет, посвященные изучению поведения несмешивающихся примесей в составном вихре, показывают, что общий вид поверхности раздела в двухслойных жидкостях зависит как от свойств самой среды, так и от различных параметров рабочей установки, таких как размеры контейнера, угловая скорость вращения и положение индуктора. На рисунке 2 представлены картины распределения масла в толще жидкости для двух различных порций несмешивающейся примеси объемом ![]() 90, 150 мл. Небольшая порция подкрашенного подсолнечного масла (
90, 150 мл. Небольшая порция подкрашенного подсолнечного масла (![]() 90 мл) частично заполняет полость каверны, выравнивая прогиб свободной поверхности (рис. 2, а). К центральному пятну масла примыкает сплошная пленка угловатой формы, от внешнего края которой отходят многочисленные узкие спиральные рукава. Спиральные рукава и группа масляных пятен разделены тонкими полосами чистой воды. При увеличении количества масла (
90 мл) частично заполняет полость каверны, выравнивая прогиб свободной поверхности (рис. 2, а). К центральному пятну масла примыкает сплошная пленка угловатой формы, от внешнего края которой отходят многочисленные узкие спиральные рукава. Спиральные рукава и группа масляных пятен разделены тонкими полосами чистой воды. При увеличении количества масла (![]() 150 мл, рис. 2, б) увеличивается прогиб поверхности раздела воздух—жидкость и увеличивается высота масляного тела, при этом возрастает площадь поверхности соприкосновения масло—воздух на периферии течения, масляная пленка становится неоднородной, на ней наблюдаются утолщенные валики спиральной формы. На внешнем крае масляной пленки начинают расти «вторичные» спиральные рукава. При любых объемах примеси, добавленной к основному течению, направление роста спиральных рукавов противоположно направлению вращения свободной поверхности составного вихря [3].
150 мл, рис. 2, б) увеличивается прогиб поверхности раздела воздух—жидкость и увеличивается высота масляного тела, при этом возрастает площадь поверхности соприкосновения масло—воздух на периферии течения, масляная пленка становится неоднородной, на ней наблюдаются утолщенные валики спиральной формы. На внешнем крае масляной пленки начинают расти «вторичные» спиральные рукава. При любых объемах примеси, добавленной к основному течению, направление роста спиральных рукавов противоположно направлению вращения свободной поверхности составного вихря [3].
а б в
Рис. 2. Распределение подсолнечного масла в составном вихре (![]() 40 см,
40 см, ![]() 7.5 см,
7.5 см, ![]() 300 об/мин): а, б)
300 об/мин): а, б) ![]() 90, 150 мл, вид сверху и сбоку, в) центральные сечения масляного тела (1– чистая вода,
90, 150 мл, вид сверху и сбоку, в) центральные сечения масляного тела (1– чистая вода, ![]() 750 об/мин, 2 –
750 об/мин, 2 – ![]() 30 мл – граница масляного тела
30 мл – граница масляного тела ![]() 770 об/мин, 3 –
770 об/мин, 3 – ![]() 30 мл – граница жидкость – воздух
30 мл – граница жидкость – воздух ![]() 770 об/мин, 4 –
770 об/мин, 4 – ![]() 2000 мл – граница масляного тела
2000 мл – граница масляного тела ![]() 720 об/мин
720 об/мин
Сравнение форм центрального сечения масляного тела и положения поверхностей раздела жидкостей и различных фаз представлено на рисунке 2в. Центральные сечения поверхностной каверны в двухслойной жидкости при различных частотах вращения диска-активатора представлены на графике. Положения свободной поверхности контакта воздух— чистая вода без добавления масла (1) и при добавлении 30 мл масла (2) практически совпадают, поскольку масляное тело фактически заполняет каверну, существовавшую в чистой жидкости, и только небольшая часть масла распределена в форме отдельных пятен по свободной поверхности. Сравнение двух кривых показывает, что масляное тело стягивает стенки каверны в более компактную область.
В экспериментах с твердотельными маркерами полипропиленовые объекты различной формы вводились уже в установившееся вихревое течение, одновременно с этим начиналась видеозапись эксперимента. На рисунке 3 а представлена схема движения маркера (черной стрелкой отмечено направление вращения диска, белой — направление вращения жидкости, белыми кружками со стрелкой отмечены положение и ориентация маркера в течение одного оборота вокруг центра вихря).
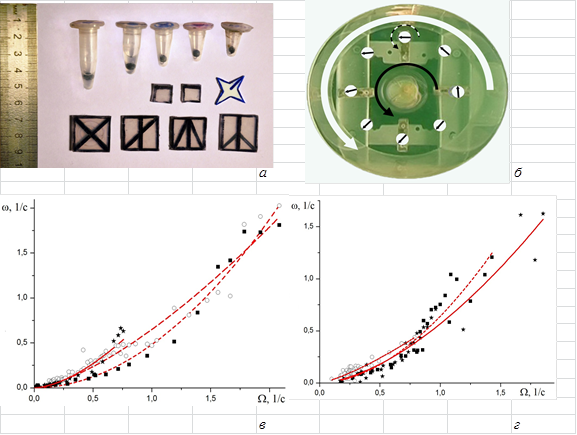
Рис. 3. Перемещение твердотельного маркера в вихревом течении (![]() 40 см,
40 см, ![]() 2,75 см,
2,75 см, ![]() 8 об/с): а) формы маркеров, б) схема движения, в, г) связь частот обращения маркера относительно центра вихря и собственного вращения маркера (каждый маркер находится на поверхности вихря отдельно), г) все три маркера находятся на поверхности вихря одновременно (0 – микропробирка; ¦ – квадратная пластинка;
8 об/с): а) формы маркеров, б) схема движения, в, г) связь частот обращения маркера относительно центра вихря и собственного вращения маркера (каждый маркер находится на поверхности вихря отдельно), г) все три маркера находятся на поверхности вихря одновременно (0 – микропробирка; ¦ – квадратная пластинка; ![]() – маркер-звезда)
– маркер-звезда)
В результате обработки отснятого материала были получены следующие основные зависимости: ω(?), ω(R), ?(R), ω(t), N(t), R(N), vφ(R), где ω – собственная частота вращения маркера (частота вращения маркера вокруг собственного центра), ? – частота обращения маркера вокруг центра вихря, R – расстояние от центра маркера до центра вихря, N – порядковый номер оборота маркера вокруг центра вихря, начиная от начала эксперимента, vφ – угловая скорость вращения маркера вокруг центра вихря. В первую очередь были проведены измерения для одиночных маркеров, помещаемых на поверхность вращающейся жидкости. Эксперимент выполнялся по три раза для каждого типа маркера при абсолютно идентичных внешних условиях. Приведенные ниже графики построены по набору данных, полученному из всех трех видеозаписей.
На рисунке 3б приведены графики зависимости частоты собственного вращения маркера ![]() от частоты обращения маркера
от частоты обращения маркера ![]() вокруг оси течения для одиночно вращающихся маркера-пробирки, маркера-квадрата и маркера-звезды и их степенные аппроксимации (табл. 1). Формы зависимостей оказываются схожи, для маркеров различной формы. Все они, помимо вращения вокруг центра вихря, вращаются вокруг своей оси. При этом более тяжелые маркеры с течением времени развивают более высокую скорость как вращения вокруг центра вихря, так и свою собственную.
вокруг оси течения для одиночно вращающихся маркера-пробирки, маркера-квадрата и маркера-звезды и их степенные аппроксимации (табл. 1). Формы зависимостей оказываются схожи, для маркеров различной формы. Все они, помимо вращения вокруг центра вихря, вращаются вокруг своей оси. При этом более тяжелые маркеры с течением времени развивают более высокую скорость как вращения вокруг центра вихря, так и свою собственную.
Несколько иная картина наблюдается при одновременном помещении на поверхность вихря всех трех типов маркеров (рис. 3в). Данный эксперимент также был проведен три раза при фиксированных внешних параметрах. Наличие взаимодействия между маркерами меняет картину их пространственного распределения в вихре, а также распределение скоростей их перемещения. Полученные зависимости аппроксимированы функцией вида ![]() . Степенные показатели аппроксимаций сохраняются неизменными в пределах погрешности для каждого типа маркера (табл. 1).
. Степенные показатели аппроксимаций сохраняются неизменными в пределах погрешности для каждого типа маркера (табл. 1).
Таблица 1
Значения коэффициентов степенной аппроксимации
|
|
Одиночные маркеры |
Маркеры в группе |
||
|
А |
В |
А |
В |
|
|
Маркер-пробирка |
0,64 ± 0,02 |
1,46 ± 0,06 |
0,60 ± 0,04 |
1,32 ± 0,07 |
|
Маркер-квадрат |
0,48 ± 0,03 |
2 ± 0,1 |
0,64 ± 0,03 |
1,9 ± 0,2 |
|
Маркер-звезда |
0,85 ± 0,02 |
1,65 ± 0,03 |
0,57 ± 0,02 |
1,65 ± 0,08 |
На рисунке 4 приведены фотографии картины переноса растворимой краски со свободно дрейфующего маркера в различные моменты времени. В процессе движения от маркера начинают распространяться два «рукава» краски. Один «рукав» направлен по направлению движения маркера, а другой — против. Следует отметить, что наличие двух «рукавов» при внесении на поверхность вихря краски наблюдалось и в других работах [1]. Картину распределения краски усложняет то, что твердотельный маркер также начинает вращаться вокруг своей собственной оси, тем самым внося возмущения в движение жидкости, что отражается на картине распространения смываемой с него краски. В процессе движения «рукава» начинают закручиваться в мелкомасштабные вихри, что существенно усложняет определение скорости распространения краски.

Рис. 4. Развитие во времени течения краски со свободно дрейфующего маркера (![]() 40 см,
40 см, ![]() 2,75 см,
2,75 см, ![]() 8 об/с): а) t = 2,56 с, г) t = 4,6 с, д) t = 16,48 с, е) t = 28,72 с, б, в) — фото маркера в увеличенном масштабе
8 об/с): а) t = 2,56 с, г) t = 4,6 с, д) t = 16,48 с, е) t = 28,72 с, б, в) — фото маркера в увеличенном масштабе
Для определения скоростей распространения переднего и заднего «рукавов» использовались координаты точек, максимально удаленных от маркера, в которых четко различалась граница краска—вода. Угловые частоты вращения вокруг центра вихря переднего и заднего концов «рукавов» краски, а также центра маркера в зависимости от времени приведены на рисунке 5.
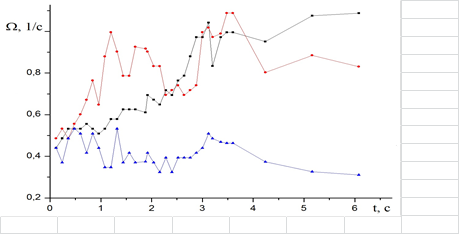
Рис. 5. Изменение угловых частот вращения вокруг центра вихря «переднего» (?) и «заднего» (^) рукавов краски, а также самого маркера (¦)
Заключение
Проведенные эксперименты показывают ярко выраженную зависимость параметров, характеризующих движение маркера на поверхности вихря, от физических свойств, формы и размеров маркера. Твердотельные маркеры обращаются вокруг центра каверны вихря и одновременно вращаются вокруг собственной оси. Угловые скорости вращения и обращения связаны функциональной зависимостью, вид которой также определяется параметрами течения и свойствами маркера (объемом, массой, размерами и формой). Однако жидкий маркер – растворимая подкраска (анилиновые чернила, штемпельная краска) не вращается относительно собственного центра, а только вытягивается. Несмешивающееся масло (касторовое, подсолнечное) в составном вихре образует масляное тело в толще и спиральные рукава на поверхности, также ориентированные навстречу основному течению.
Таким образом, перенос маркера в вихревом течении качественно и количественно зависит от его фазового состояния (твердый, жидкий) и формы. Проведенные эксперименты показали, что при визуализации течений в жидкости при помощи маркеров необходимо учитывать характеристики самих маркеров и вносить соответствующие поправки при расчетах.
Работа выполнена при финансовой поддержке РФФИ №14-01-00015-а.
Рецензенты:
Карев В.И., д.т.н., зам. директора на научной работе ФГБУН Института проблем механики имени А.Ю. Ишлинского Российской академии наук, г. Москва;
Лапшин В.Б., д.ф.-м. н., директор ФГБУ Института прикладной геофизики Росгидромета, г. Москва.
Библиографическая ссылка
Будников А.А., Чаплина Т.О. СПЕЦИФИКА ДВИЖЕНИЯ ТВЕРДОТЕЛЬНЫХ И ЖИДКИХ МАРКЕРОВ В ВИХРЕВОМ ТЕЧЕНИИ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18910 (дата обращения: 26.04.2024).



