В концепции развития образования подчеркнуто, что возможность получения качественного образования продолжает оставаться одной из наиболее важных жизненных ценностей граждан, решающим фактором социальной справедливости и политической стабильности и представлены приоритетные задачи, решение которых приведет к реализации этой цели. Основной задачей современного образования является формирование и развитие личности, способной к саморазвитию.
Для этого развитие должно протекать в различных направлениях, в т.ч. и в направлении развития отдельных видов мышления. Среди последних особое значение в жизни каждого человека имеет пространственное мышление, т.к. именно оно способствует возможности проектирования, воображения и представления различных объектов и явлений.
Пространственное мышление – это, по мнению психологов, методистов-математиков:
-
мыслительный процесс, представляющий по своему содержанию обобщенное и опосредованное отражение пространственных свойств и отношений объекта, включенного в этот мыслительный процесс;
-
многократные мыслительные действия с образами, требующие их динамичности, интуитивное определение, какие именно действия целесообразно выполнять для получения нужного результата;
-
процесс опознавания реально представленных объектов или их изображений и мысленное создание на этой основе таких же объектов, но иначе расположенных, или конструирование новых, включающий в себя также воссоздание пространственных объектов по некоторым их элементам;
-
разновидность образного мышления, основу которого составляют геометрические образы и основная функция которого оперирование образами в математическом (абстрактном, условно-схематическом) пространстве.
В своих работах [3, 4, 5, 6, 10,17] мы уже анализировали различные подходы, имеющие место в науке, к развитию пространственного мышления. В данной статье остановимся на рассмотрении одного из средств развития – системы задач.
О.Н. Орлянской [12] были проанализированы трактовки систем задач, представленные российскими учеными-методистами, и выделены следующие их характеристики:
-
общность – задачи подчинены общей идее (методу решения, кругу используемых понятий, дидактическим назначениям и т. д.) или теме общего курса, обладающей разным уровнем глобальности;
-
способ построения (аналогия, обобщение, конкретизация и др.) – каждая задача обобщена предыдущей, или ее конкретизирует, или является аналогом, или является ключевой задачей;
-
уровень организации – строго детерминированное расположение уровней связей между задачами;
-
связность элементов в системе – возможность графически представить совокупность задач связным графом;
-
полнота – совокупность задач включает в себя задачи на все изучаемые понятия, факты, способы деятельности, в том числе мотивационные, подходящие под понятие, на аналогию, следствия из фактов и прочие;
-
целевая достаточность – достаточное количество задач для тренинга в классе и дома; аналогичных задач для закрепления метода решения; задач для индивидуальных и групповых заданий разной направленности; задач для самостоятельной (в том числе исследовательской) деятельности учащихся; задач для текущего и итогового контроля с учетом запасных вариантов и т. д.;
-
целевая ориентация – определение места каждой задачи и назначения в блоке уроков;
-
рядоположенность (последовательность расположения) – наличие усложнений, разветвлений.
Рассмотрим подходы различных ученых-методистов к составлению систем задач (упражнений, заданий и т.п.), направленных на развитие пространственного мышления или его компонентов.
Учитывая особенности пространственных представлений, их отличие от первичных образов, Н.С. Подходова [15] выделяет следующие типы заданий и условия их выполнения, учитывающие особенности формирования представлений как обобщения перцептивных образов:
1. Задания на развитие представлений должны: а) выполняться в отсутствии наглядной основы; б) предлагаться не только по линии образов, отражающих различную фактуру моделей, цвет, материал и т.п., но и по линии разнообразия положений моделей фигур в образах, ведь положение фигуры в пространстве не определяет ее название.
2. Задания на представливание: а) полезно выполнять с закрытыми глазами, но, помогая себе, если нужно, руками, т.е. жестикулируя; б) при их выполнении требуют тишины и отсутствия напряженности у учащихся; в) предлагается составлять самим учащимся; г) выполняют функцию обучения переводу с вербального языка на язык образов и наоборот (в случае составления таких задач учащимися), а значит способствуют развитию умения описывать пространство и внимательному отношению к тексту любой задачи; д) неэффективны в форме заданий типа «кто быстрее».
3. Задания на проверку сформированности представлений наиболее эффективны в форме практической деятельности, создания вещественных моделей (в случае объемных фигур) или рисунков (в случае плоских фигур) соответствующих геометрических объектов.
А. Пардала [13] выделяет виды упражнений, дидактическим назначением которых является формирование и развитие пространственных представлений учащихся: математические игры, связанные с пространственными представлениями; исследование конкретных геометрических объектов - фигур и преобразований; конструктивные задачи; прикладные задачи; проекционные стереометрические задачи; задачи на проектирование геометрических тел, построение сечений; диагностические задачи на проверку сформированности пространственных представлений.
В исследовании А.Я. Цукаря [18] охарактеризованы задачи на пространственное воображение следующих видов: оценивание формы и размеров фигуры; отыскание изображения из нескольких данных для предъявленного объекта; нахождение объекта из некоторого набора, соответствующего данному изображению; завершение изображения известного объекта по его фрагменту; идентификация различных изображений одного и того же пространственного объекта; построение проекций заданной фигуры; узнавание фигуры по ее проекциям; построение изображения объекта по его проекциям; определение взаимного расположения нескольких фигур по их изображению; изображение объекта по его описанию; изготовление модели по ее чертежу, по предъявленному объекту, по описанию; узнавание и изображение объекта, полученного (мысленным) изменением (с помощью поворота, симметрии, параллельного переноса) положения заданного; узнавание и изображение фигуры, составленной из заданных по известному правилу; изображение пересечения заданных фигур (в том числе после мысленного их перемещения); изображение частей фигур после ее мысленного расчленения.
С.Б. Верченко в своем исследовании [7] представила следующую систему заданий, способствующих развитию пространственного воображения: на распознавание моделей; на рассмотрение чертежей; на одновременную работу с моделью, чертежом и рисунком.
В исследованиях Е.Н. Кабановой-Меллер, А.Д. Ботвинникова, И.С. Якиманской [1, 11] подчеркивается, что своих наиболее развитых форм пространственное мышление достигает в процессе деятельности с графическим материалом (чертежом), основанный на создании и преобразовании зрительных образов и заключающийся в чтении, создании и преобразовании чертежа. В основе правильного чтения чертежа лежит умение рассматривать одну и ту же фигуру с разных точек зрения, т.к. определить форму изображенного на чертеже объекта можно только путем неоднократного анализа под углом зрения разных проекций. Однако, как показывают ученые, овладение приемами восприятия пространственных образов по их графическим изображениям, как бы эффективны они не были, не обеспечивают еще успешности оперирования ими.
Методисты-геометры (А.Б. Василевский, Г.Д. Глейзер, С.В. Петров и др.) [2, 9, 14] предлагают в работе с учащимися использовать задачи, решаемые по чертежу, на мысленное представление объемной фигуры по отдельным ее элементам, на построение разверток объемных фигур, выполнение построения изображений некоторых объемных фигур на плоскости, построение сечений пространственных фигур. Исследователи считают решение задач на изображение пространственных фигур наиболее эффективным средством развития пространственных представлений, воображения.
Укажем некоторые действия (механизмы), направленные на развитие умений создавать и оперировать образами:
-
создание первичных образов;
-
распознавание образов пространственных объектов или их моделей (графических или реальных);
-
воссоздание образов пространственных объектов или их моделей по некоторым их элементам;
-
изменение расположения образов представленных объектов;
-
конструирование новых образов на основе представленных – преобразование образов (изменения структуры образа; изменения пространственного положения и структуры образа) и др.
Сам реальный объект, его мысленный образ и его модели (например, изображение) находятся не во взаимно-однозначных отношениях. Распознавание объектов есть процесс взаимного отождествления данного объекта, его образа и модели. Например, «узнавание» объекта по его изображению. Под созданием моделей (графических или реальных) представленных пространственных объектов понимаем, например, изображение (создание графической модели) объекта. «Воссоздать» графическую модель по некоторому фрагменту – это значит, дополнить, завершить изображение какого-либо объекта.
Под оперированием пространственными образами методистами (И.Г. Вяльцевой и др.) [8] понимается мыслительная деятельность, направленная на активизацию исходных образов в нужном направлении, их перестройку, видоизменение, трансформацию и создание на этой основе новых образов, а основным средством графической передачи образов авторы считают чертеж. Поэтому знание способов изображения пространственных фигур на плоскости создает необходимые предпосылки для воссоздания пространственных образов по восприятию их изображений (чертежей) и выполнению мысленных действий над ними.
Мы выделяем четыре вида задач на развитие пространственного мышления учащихся, связанных с реальными объектами, их изображениями, моделями и др.
Для рассмотрения таких задач, введем несколько дополнительных понятий. Объект, подлежащий какому-либо моделированию и затем воспроизведению, будем называть прообразом, а плоскую фигуру, воспроизводящую и представляющую прообраз – образом. Образ, представляющий объект на плоской поверхности, будем называть изображением этого объекта.
Итак, а) задачи на создание пространственного образа (определенного или неопределенного прообраза), определение его вида и свойств (задачи первого вида); б) задачи, в которых требуется установить соответствие между образом и прообразом, или между двумя различными образами (задачи второго вида); в) задачи, решение которых начинается с рассмотрения уже определенного образа, и заключается либо в восстановлении прообраза, либо в определении свойств прообраза (задачи третьего вида); г) задачи на мысленное преобразование пространственных образов (задачи четвертого вида).
Задача 1 (первого вида): Отмеченные точки – вершины некоторого многогранника (рис.1). Начертите многогранник так, чтобы грань BCD была видимой, а грань АКО – невидимой.
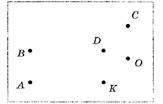
Рис.1
Сложность задачи заключается в том, что вид многогранника не определен. Поэтому у учащихся могут возникнуть разные образы.
Вопрос: можно ли не представляя многогранник выполнить задание. Конечно, на начальном этапе выполнения задания можно воспользоваться правилами изображения видимых и невидимых объектов, но на заключительном этапе все-таки необходимо представить результат (создать образ) с целью определения возможности существования такого многогранника.
Задача 2 (второго вида): На рисунке 2 представлена развертка кубика. Определите, изображение какого кубика из представленных на рисунке 3 может быть получено из этой развертки.
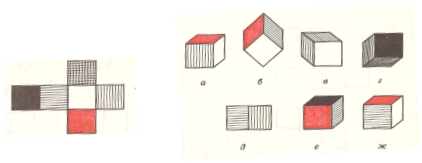
Рис. 2 Рис. 3
При решении данной задачи необходимо сопоставить две модели куба: изображение развертки и наглядное изображение. При решении задачи можно: 1) склеить по изображению развертки модель куба, обозначить соответствующим образом грани и вращая модель сопоставить с наглядными изображениями; 2) мысленно сопоставить наглядные изображения куба и его развертку. Во втором случае возможно два варианта: 1) создать мысленный наглядный образ по изображению развертки, мысленно его вращать, сопоставляя с наглядными изображениями; 2) мысленно «разворачивать» поверхность куба по наглядным изображениям, мысленно преобразовывать развертки и сопоставлять с данным изображением.
Задача 4 (третьего вида): Изобразите фигуру, получающуюся при вращении равностороннего треугольника вокруг прямой, параллельной оси треугольника и проходящей через его вершину.
Задача 5 (четвертого вида): Как могут располагаться в пространстве два отрезка, чтобы их параллельными проекциями были фигуры, изображенные на рисунке 4?
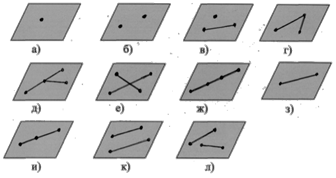
Рис.4
Кроме этого мы выделили две группы задач базового уровня: подготовительные и основные и две группы задач профильного (углубленного) уровня: основные и дополнительные.
|
базовый уровень обучения решению задач на пространственное мышление (изучение элементов геометрии в 5-6 кл., геометрии в 7-9 кл.) |
профильный уровень обучения решению задач на пространственное мышление (изучение геометрии в 7-11 кл.) |
||||
|
подготовительные задачи (задачи четырех видов, предлагаемые учащимся на пропедевтическом и первом систематическом этапах обучения геометрии) |
основные задачи (задачи четырех видов, предлагаемые учащимся на пропедевтическом и первом систематическом этапах обучения геометрии) |
основные задачи (задачи четырех видов, предлагаемые учащимся на первом и втором систематических этапах обучения геометрии) |
дополнительные задачи (задачи четырех видов, предлагаемые учащимся на первом и втором систематических этапах обучения геометрии) |
||
|
задачи, предлагаемые учащимся до введения понятий «вид», «проекция» |
задачи, предлагаемые учащимся решение после введения понятий «вид», «проекция» |
задачи, предлагаемые учащимся до введения понятий «вид», «проекция» |
задачи, предлагаемые учащимся после введения понятий «вид», «проекция» |
||
Подготовительными задачами профильного уровня являются основные задачи базового уровня.
В каждой из четырех групп задач (подготовительные базового уровня, основные базового уровня, основные профильного уровня, дополнительные профильного уровня) предлагаются задачи четырех указанных выше видов.
Задачи на развитие пространственного мышления мы рекомендуем предлагать учащимся при изучении следующих тематических блоков курса геометрии:
-
Взаимное расположение точек, прямых и плоскостей;
-
Взаимное расположение плоских и пространственных фигур;
-
Многоугольники и многогранники;
-
Тела вращения;
-
Объединение и пересечение фигур. Сечения;
-
Моделирование пространственных фигур;
-
Преобразования плоскости и пространства;
-
ГМТ.
Разработанной нами системе задач присущи все необходимые характеристики:
-
общность – задачи подчинены общей идее развитию пространственного мышления;
-
способ построения – каждая задача обобщена предыдущей, или ее конкретизирует, или является аналогом, или является ключевой задачей;
-
уровень организации – строго детерминированное расположение уровней связей между задачами;
-
связность элементов в системе – возможность графически представить совокупность задач связным графом (в нашем случае представлена таблица);
-
полнота – совокупность задач включает в себя задачи на все понятия, связанные с проектированием, изображением и т.п.;
-
целевая достаточность – наличие достаточного количества задач для тренинга; аналогичных задач для закрепления метода решения; задач для индивидуальной и групповой работы; задач для самостоятельной (в том числе проектно-исследовательской) деятельности учащихся и т. д.;
-
целевая ориентация – место каждой задачи определено в соответствии с уровнями и основными действиями, направленными на развитие умений создавать и оперировать образами;
-
рядоположенность (последовательность расположения) – задачи четырёх видов распределены по уровням (базовому и профильному).
В процессе педагогического эксперимента мы показали, что использование данной системы задач при обучении геометрии и её элементам способствует развитию пространственного мышления учащихся.
Рецензенты:
Санина Е.И., д.п.н., профессор, профессор кафедры психологии и педагогики ФГБОУ ВПО «Российский университет дружбы народов», г. Москва;
Ниматулаев М.М., д.п.н., доцент кафедры «Информатика и программирование» ФГБОУ ВПО «Финансовый университет при Правительстве Российской Федерации», г. Москва.
Библиографическая ссылка
Василенко А.В. СИСТЕМАТИЗАЦИЯ ЗАДАЧ НА РАЗВИТИЕ ПРОСТРАНСТВЕННОГО МЫШЛЕНИЯ УЧАЩИХСЯ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=17384 (дата обращения: 16.01.2026).



