Включение в процесс обучения математике компьютерных средств ведёт к изменению состояния функционирования и проектирования образовательного пространства. В этой связи перед методической наукой стоят задачи, связанные с методической поддержкой эффективного использования компьютера в учебном процессе по математике. Современная теоретическая и практическая направленность поисков в решении этой проблемы определяется двумя линиями: визуализацией учебного материала и развивающим обучением. В первом направлении изучаются методические условия использования средств визуализации при изучении нового материала, наглядной демонстрации динамики изучаемых процессов, графической интерпретации исследуемых закономерностей и т.д. (В.А. Далингер, Т.Ф. Сергеева, Иванов С.Г. и др.). Во втором направлении изучаются возможности: индивидуализации; виртуальных лабораторий; контроля, тренажёра и пр. (В.В. Дубровский, М.В. Шабанова и др.).
И хотя обозначенные линии охватывают достаточно большой спектр проблем использования компьютера в обучении математике, при всем том в каждом из направлений, по мнению многих учёных, остаются актуальными вопросы, связанные с отбором содержания учебного материала для компьютерных программ и принципами его структурирования, с целью усиления той или иной функции обучения математике.
В указанных обстоятельствах изучение компьютерного эксперимента как дидактической единицы методической системы обучения математике, ориентированного на воспитание ученика-исследователя, представляет для теории и методики обучения математике определённый интерес.
Содержание исследования
Структуру методической системы формирования исследовательской деятельности учащихся в процессе обучения их математике можно описать в виде связей и отношений между целями, содержанием, методами, формами и средствами обучения, которые интерпретируются в процессе обучения в виде дидактических отношений между: предметным содержанием обучения и содержанием исследовательской деятельности ученика, между содержанием обучения и учеником, между учителем и учеником. Следовательно, анализ компьютерного эксперимента как дидактической единицы необходимо осуществлять как на уровне каждого компонента системы, так и на уровне структуры, то есть связей.
Концептуальной основой ФГОС второго поколения является системно-деятельностный подход, в соответствии с которым на первый план в системе целей математического образования выходит деятельное содержание, представленное в виде способов деятельности по освоению математических знаний (языка, методов математики и пр.), по приобретению опыта творческой деятельности и т.д. Современная психология рассматривает знания как деятельность, оценённую с точки зрения её результата. В таком понимании способы деятельности должны быть прямым продуктом взаимодействия с некоторым объектом, носителем способа деятельности [3, С.9]. То есть этот объект должен выступать как носитель деятельности, это с одной стороны, а с другой, как средство усвоения этой деятельности. А поскольку компьютерный эксперимент по математике предполагает владение приёмами и способами: наблюдения, анализа, перевода наблюдаемых фактов на язык математики (моделирования), выдвижения гипотетических предположений, способами конструирования и поиска новых задач, приводящих к дальнейшим экспериментам, то с точки зрения целей и содержания обучения, ориентированного на воспитание ученика-исследователя, компьютерный эксперимент выступает и как носитель способов и приёмов исследования, и как средство их усвоения.
Рассмотрению компьютерного эксперимента как дидактической единицы способствуют и исследования в области методологии математики. Так, например, в современных фундаментальных исследованиях в этой области, где одним из направлений является изучение особенностей познания математических объектов, способах «бытия» этих объектов и пр., был обоснован новый взгляд на механизм познания сущности явлений математики. Показано, что познание не является актом непосредственного «отражения», а представляет собой процесс моделирования исследуемого явления с помощью предугаданной схемы [2, С.9]. В этой связи необходимо пересмотреть акценты в средствах получения знаний об исследуемом объекте, то есть в практике учебного исследования по математике необходимо усилить экспериментальную и конструирующую составляющие. Действительно, «… всё здание математики, как всякой другой науки, построено на гипотезах, правомерность которых во многих случаях весьма проблематична. На это обстоятельство обратил внимание ещё Ф. Энгельс» [2, С. 5,6]. Тогда ввиду того, что компьютерное математическое экспериментирование предполагает практику получения знания об объекте исследования, выявления свойств и зависимостей в этом объекте, то компьютерный эксперимент может быть средством и получения, и освоения знаний по математике.
На осмысление сущности компьютерного эксперимента в ситуации формирования способов исследовательской деятельности школьника оказывают результаты по изучению проблем организации познавательной самостоятельности ученика. В работах многих ученых, исследовавших результативность процесса становления знаний (В.В. Давыдова, В.И. Загвязинцева и др.) показано, что эффективность формирующего процесса напрямую зависит от степени самостоятельности в деятельности ученика как участника этого процесса. Но степень самостоятельности в деятельности обучающегося определяется его познавательными интересами (Ю.К. Бабанский, М.А. Данилов и др.), которые стимулируются и развиваются мотивами (П.И. Пидкасистый, А.В. Усова). А поскольку компьютерные экспериментирования позволяют вывести ученика в исследовательскую позицию, вовлечь его в самостоятельный исследовательский поиск [10,12], то компьютерный эксперимент в процессе формирования исследовательской деятельности учащихся может быть способом стимулирования и мотивации познавательной деятельности ученика, это с одной стороны.
С другой, согласно теории интериоризации, формирование нового для человека умственного умения начинается с внешнего действия с материальными объектами. Действие формируется по образцу, причем исходной формой действий не обязательно являются действия с реальными объектами: в равной мере эту функцию выполняют «материализованные» действия с изображениями вещей, которые воспроизводят некоторые их свойства и отношения, необходимые для действия. В исследованиях Л.Л. Гуровой [1] и ее соратников о взаимодействии между мысленными и практическими операциями было выявлено, что практические операции с материальными объектами имеют собственную функцию в формировании мыслительных операций, которые и составляют основу развития самостоятельности мышления. Это значит, что компьютерный эксперимент может выступать способом организации и управления учебно-познавательной деятельностью ученика, и, как следствие, оказывать положительное влияние на становление его исследовательской активности.
Согласно исследованиям Г.И. Саранцева, методы обучения математике можно трактовать как форму движения содержания обучения, которые в предметных методиках выступают в качестве способов организации учебного материала и взаимодействия обучающего и учащихся, направленных на решение образовательных задач [4, С. 158]. А поскольку компьютерный эксперимент может выступать в качестве способа организации и управления познавательной деятельностью ученика, то его можно рассматривать и как форму проявления методов обучения.
Итак. Осмысление характера компьютерного эксперимента на уровнях целей, содержания, форм и средств обучения позволяет утверждать, что компьютерный эксперимент обеспечивает функциональную связь всех компонентов методической системы формирования исследовательской деятельности в процессе обучения математике (таблица).
Теоретическая модель дидактического объекта «компьютерный эксперимент»
|
КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ КАК ДИДАКТИЧЕСКАЯ ЕДИНИЦА
|
|
|
УРОВНИ ДИДАКТИЧЕСКОГООБЪЕКТА
|
ХАРАКТЕРНЫЕ ПРОЯВЛЕНИЯ ДИДАКТИЧЕСКОГО ОБЪЕКТА В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ
|
|
|
Как носитель способов целенаправленного формирования исследовательской деятельности учащихся в процессе обучения их математике |
|
|
Как средство целенаправленного формирования исследовательских умений обучающихся |
|
|
Как способ организации исследовательской деятельности учащихся в процессе обучения их математике |
|
|
Как форма реализации методов обучения математике |
Проецируя полученную теоретическую модель на содержание учебного материала курса математики, можно организовать целесообразное использование компьютерного эксперимента в формировании исследовательской деятельности ученика при достижении ими в учебном процессе основных образовательных результатов.
Проиллюстрируем на примерах реализацию модели. Для этой цели нами разработан в среде «MathCAD» программный продукт по курсу стереометрии «динамические задачи» (рисунок) [5].
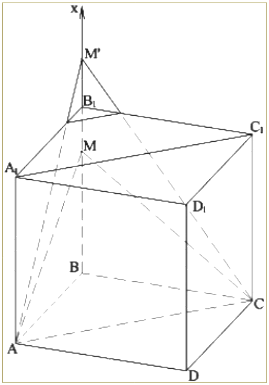
Динамическая модель построения сечения куба плоскостью
Суть этого продукта заключается в следующем. Зафиксировав любые две точки на поверхности куба или в плоскостях его граней, можно правой кнопкой двигать третью точку либо по прямой, содержащей ребро куба, либо в плоскости его грани; левой поворачивать куб и построенное сечение в различные положения (вращать вокруг рёбер, оси куба и пр.), или двигать плоскость построенного сечения в задуманном направлении. В результате ученик может моделировать различные положения трёх точек, через которые проводится сечение, может экспериментировать с положением точек на поверхности куба, с положением секущей плоскости.
В соответствии с теоретической моделью, в учебном процессе компьютерный эксперимент может выполнять разные функции: служить средством открытия нового знания, быть средством стимулирования поисковой активности ученика, быть средством целенаправленного формирования приёмов исследования, выступать одной из форм проявления исследовательского метода обучения, служить средством контроля усвоения содержания обучения и пр. В зависимости от учебной ситуации, эти функции могут быть взяты как в совокупности, так и отдельно от других. Рассмотрим примеры некоторых ситуаций.
Учебная ситуация 1. Ученик не владеет методом построения сечения многогранников плоскостью, но знает аксиомы стереометрии и следствия из них. Учитель перед началом эксперимента предлагает учащимся решить задачу (без средств компьютерной поддержки):
Предметная задача. В кубе АВСD А1В1С1D1 точка М расположена на ребре ВВ1. Постройте сечение куба АВСD А1В1С1D1 плоскостью, содержащей вершины А,С и точку М данного куба.
После проверки и обсуждения решения задачи учитель предлагает ученикам осуществить эксперимент:
Предметная задача. В кубе АВСD А1В1С1D1 точка М движется по прямой, содержащей ребро ВВ1. Исследуйте вид сечения данного куба плоскостью АМС в зависимости от положения точки М. Выясните, от чего зависит вид сечения куба плоскостью. Попробуйте предложить метод построения сечения куба плоскостью.
Методическая цель эксперимента заключается в том, что постановкой соответствующей учебной задачи в контекстной форме перед учеником ставится мыслительная задача (проанализировать возможные пространственные отношения), которая решается с опорой на динамический чертеж, тем самым мы добиваемся того, что осуществляется контролирующая функция мышления, это, во-первых. А во-вторых, ученик может наблюдать изменение вида многоугольника, полученного в сечении куба плоскостью, может поэкспериментировать с положением точек на поверхности куба, а затем самостоятельно сформулировать правило построения сечения куба плоскостью методом следов.
Учебная ситуация 2. Ученик владеет методом следов построения сечений многогранников.
Учитель предлагает построить сечение куба плоскостью, перпендикулярной его диагонали, а затем выполнить параллельный перенос построенного сечения на вектор, перпендикулярный диагонали куба. Ученику предлагается пронаблюдать за изменением вида сечения и попробовать ответить: отчего такое происходит (это явление бифуркации).
Методическая цель эксперимента заключается в том, что постановкой соответствующей мыслительной задачи (проанализировать возможные пространственные отношения), которая решается с опорой на динамический чертеж, мы добиваемся того, что осуществляется контролирующая функция мышления, это, во-первых. А во-вторых, ученик может наблюдать изменение вида многоугольника, полученного в сечении куба плоскостью, может самостоятельно познакомится с новым понятием современной математики.
Учебная ситуация 3. Ученик владеет методами построения сечений многогранников.
Учитель предлагает построить сечение куба АВСD А1В1С1D1 плоскостью, проходящей через точки М (М расположена на ребре ВВ1) и точки А,С. Затем поэкспериментировать, поворачивая куб так, что на экране можно увидеть только отрезок, на который проецируются стороны сечения. В ходе эксперимента нужно выяснить, всегда ли можно восстановить сечение по полученным проекциям?
Методическая цель эксперимента заключается в постановке мыслительной задачи, выводящей ученика в исследовательскую позицию, где он учится высказывать гипотетические предположения, опровергать или доказывать их.
В рамках проекта «Внедрение в образовательное пространство учебных учреждений города Павлодара и Павлодарской области технологии формирования исследовательской деятельности в условиях индивидуализированного обучения» (Казахстан, 2009–2014 гг.) было выявлено, что наибольшая эффективность в использовании компьютерного эксперимента в обучении математике достигается на этапе введения математического понятия (функция демонстрации), при обучении доказательству теорем (при осознании и принятии проблемы, формулировании гипотезы). Однако при обучении решению задач роль компьютерного эксперимента снижается. Мы отметили, что с усложнением условия задачи ученик не может на основе эксперимента высказать предположение о способе её решения и тем более её решить.
Подтверждением полученных экспериментальных результатов являются теоретические исследования проблемы соотношения образного и логического в познавательных процессах. В частности, в работах А.Н. Леонтьева, Т.Г. Егорова и их сотрудников ставится вопрос о выявлении действительной роли наглядного материала в учебной деятельности школьника: объективные и субъективные задачи деятельности могут не совпадать между собой. В работах Е.Н. Кабановой-Меллер представлены примеры отрицательного влияния зрительного образа на решение задачи: в силу недостаточного обобщения существенных признаков демонстрируемых объектов, учащиеся затрудняются с помощью этого наглядного материала решить задачу.
Аналогичные наблюдения и их анализ представлены в работах В.И. Зыковой, Н.А. Менчинской. А в исследованиях Л.Л. Гуровой на материале стереометрических позиционных задач доказано, что зрительное восприятие играет положительную роль только в том случае, если у решающего сформировались операции выбора, но он затрудняется осуществить этот выбор по представлению.
Учитывая теоретические и практические исследования, можно утверждать, что самостоятельная функция наглядного пособия описанного выше конструктивного выражения в решении задачи может иметь положительное влияние только в случае решения учащимися элементарной по содержанию задачи. С усложнением условий задачи наглядное пособие само по себе уже не может служить отправным моментом, предопределяющим положительный исход, поскольку решающее значение в этом случае приобретает сформированность необходимых мыслительных действий, то есть логический фактор. Использование динамических моделей является наиболее эффективным при условии отведения им опорной функции в общей системе формирования мыслительных действий и при выводе ученика в исследовательскую позицию. Именно при этих условиях достигается необходимое соответствие между абстрактными и образными компонентами мышления, и наглядные динамические чертежи действительно помогают научить решать задачи.
Выводы
Итак, результаты теоретического и практического исследования тезисно можно представить следующим образом:
1. Компьютерный эксперимент, как дидактический объект, необходимо рассматривать на четырёх уровнях.
2. В учебном процессе компьютерный эксперимент может выполнять разные функции: служить средством открытия нового знания, быть средством стимулирования поисковой активности ученика, быть средством целенаправленного формирования приёмов исследования, выступать одной из форм проявления исследовательского метода обучения, служить средством контроля усвоения содержания обучения и пр. В зависимости от учебной ситуации эти функции могут быть взяты как в совокупности, так и отдельно от других.
3. Экспериментально и теоретически доказано, что компьютерный эксперимент не оказывает существенного влияния на формирование умений решать задачи.
4. Наибольшая эффективность использования компьютерного эксперимента в учебном процессе отмечена на этапах введения понятий, на этапах высказывания гипотетических предположений.
Рецензенты:
Жафяров А.Ж., д.ф.-м.н., заведующий научной лабораторией профильного образования Новосибирского государственного педагогического университета, г. Новосибирск;
Аммосова Н.В., д.п.н., профессор, ФГБОУ ВПО «Астраханский государственный университет», г. Астрахань.
Библиографическая ссылка
Таранова М.В. КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ КАК ДИДАКТИЧЕСКАЯ ЕДИНИЦА МЕТОДИЧЕСКОЙ СИСТЕМЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ УЧАЩИХСЯ // Современные проблемы науки и образования. 2015. № 2-1. ;URL: https://science-education.ru/ru/article/view?id=17360 (дата обращения: 06.07.2025).



