Функция физических свойств материала, в плоскости Oxy, является 2-периодической; плоскость можно представить состоящей из множества одинаковых прямоугольников – ячеек (рис. 1,2). Макросвойства - механические свойства однородного макроматериала эквивалентного композитному периодическому материалу.
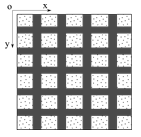
Рис. 1. Материал, армированный
Постановка задачи
На конструкцию, изготовленную из материала, армированного периодической решеткой (рис. 1.), действует некоторая система нагрузок.
В каждой точке конструкции выполняются уравнения равновесия:
![]() (1)
(1)
где ![]() - объемные силы, а
- объемные силы, а ![]() - напряжения, определяющиеся по закону Гука для анизотропной среды:
- напряжения, определяющиеся по закону Гука для анизотропной среды:
![]() (2)
(2)
где ![]() - тензор упругости, который внутри каждой упругой среды непрерывно меняется, а на границах сред претерпевает скачки. Уравнения (1)-(2) обезразмерены по правилам:
- тензор упругости, который внутри каждой упругой среды непрерывно меняется, а на границах сред претерпевает скачки. Уравнения (1)-(2) обезразмерены по правилам:
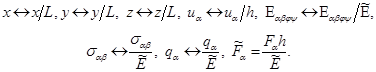 (3)
(3)
![]() (4)
(4)
где ![]() - размер ячейки,
- размер ячейки, ![]() - характерный размер тела.
- характерный размер тела.
На границе перехода от одной упругой среды к другой непрерывны перемещения и контактные напряжения:
![]() ,
, ![]() ,
, ![]() (5)
(5)
где ![]() - контактные напряжения, которые по определению вычисляются по следующей формуле
- контактные напряжения, которые по определению вычисляются по следующей формуле

Рис. 2. Периодическая ячейка
![]() . (6)
. (6)
Заданы граничные условия.
В ячейке вводится локальная система координат ![]() , координатные оси параллельны осям глобальной системы координат (рис. 2).
, координатные оси параллельны осям глобальной системы координат (рис. 2).
Асимптотическое приближение решения краевой задачи (1)-(6) в соответствии с работой 1 имеет вид при условии ![]() :
:
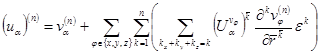 , (7)
, (7)
![]()
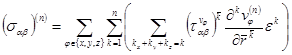 ,
, ![]() (8)
(8)
здесь ![]() - номер асимптотического приближения,
- номер асимптотического приближения, ![]() - решение для тела, состоящего, из макроматериала,
- решение для тела, состоящего, из макроматериала, ![]() - периодическая компонента решения (ячейковые перемещения),
- периодическая компонента решения (ячейковые перемещения), ![]() - ячейковые напряжения,
- ячейковые напряжения, ![]() - вектор, определяемый таким образом:
- вектор, определяемый таким образом:
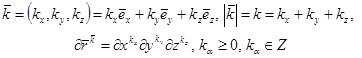 (9)
(9)
Для определения макрохарактеристик необходимо найти периодическую компоненту решения. Ячейковые перемещения определяются решением девять краевых задач, для ![]() :
:
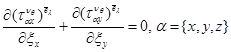 (10)
(10)
закон упругости на ячейке –
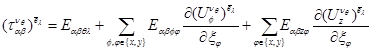 11)
11)
условия непрерывности ячейковых функций внутри ячейки на границе различных сред –
![]() (12)
(12)
условие периодичности ячейковых функций –
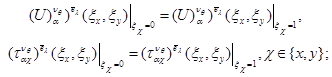 (13)
(13)
условие нормировки решения –
![]() (14)
(14)
где ![]() - интеграл от какой-то величины по ячейковым переменным, взятый по всей ячейке, усреднение этой величины по ячейке:
- интеграл от какой-то величины по ячейковым переменным, взятый по всей ячейке, усреднение этой величины по ячейке:
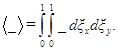 (15)
(15)
Решением девяти краевых задач (10)-(13) являются восемнадцать ячейковых перемещений ![]() , для них выполняются равенства:
, для них выполняются равенства:
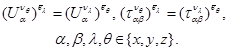 (16)
(16)
То есть, необходимо решить не девять, а шесть краевых задач (10)-(13).
Из решений краевых задач (10)-(13) вычисляются макрохарактеристики материала (обозначение – волнистая верхняя черта) по формуле:
 (17)
(17)
Выведение формул для макрохарактеристик в случае 3-периодической композитной среды приведено в работе [3].
Результаты
Построены зависимости упругих свойств макроматериала от коэффициента армирования для композитных материалов армированных решетками двух форм: тетрагональной (рис. 3а) и гексагональной (рис. 3б). Свойства материалов: модуль Юнга связующего 40 МПа, коэффициент Пуассона связующего 0.35, модуль Юнга решетки 393 МПа, коэффициент Пуассона 0.4. Что примерно соответствует структуре грунт-георешётка.
Эти зависимости представлены на рисунках 5-10. Значения макросвойств армированного грунта получены по формуле (17), ячейковые функции получены решением краевых задач (10)-(13) методом конечных элементов.
Коэффициент армирования (КА) – отношение площади сечения решетки к общей площади ячейки.
![]() , (18)
, (18)
![]() - площадь сечения решетки,
- площадь сечения решетки, ![]() - площадь ячейки. Площадь сечения решетки изменяется варьированием толщины d.
- площадь ячейки. Площадь сечения решетки изменяется варьированием толщины d.
В работах [1], [2] приведены аналогичные зависимости для материалов, армированных волокнами. В таблице 1 представлен расчет макросвойств для композитного материала армированного тетрагональной решеткой при КА = 0.009975. В первом столбце макросвойства рассчитаны по формулам из статьи [3], во втором по формулам из статьи [4]. В третьем, макросвойства рассчитаны числено, методом ячейковых функций из данной статьи. Четвертый столбец – среднее арифметическое свойств материалов, входящих в состав композита.
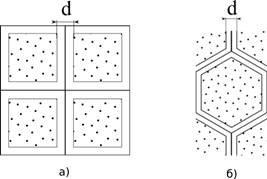
Рис. 3. Типы армирующих решеток: а) тетрагональная, б) гексагональная.
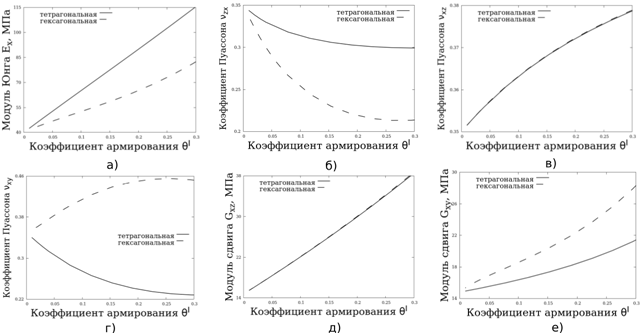
Рис. 4. Зависимость механических макросвойств от коэффициента армирования: а) Модуль Юнга ![]() , б) Коэффициент Пуассона
, б) Коэффициент Пуассона ![]() , в) Коэффициент Пуассона
, в) Коэффициент Пуассона ![]() , г) Коэффициент Пуассона
, г) Коэффициент Пуассона ![]() , д) Модуль сдвига
, д) Модуль сдвига ![]() , е) Модуль сдвига
, е) Модуль сдвига ![]() .
.
Таблица 1
Механические макросвойства, рассчитанные различными методами, при коэффициенте армирования 0.009975
|
Упругие константы |
Методы расчета |
|||
|
Кинематический [3] |
Статический [4] |
Ячейковых функций |
Среднее арифметическое |
|
|
|
42.57 |
43.56 |
42.56 |
43.52 |
|
|
43.54 |
43.54 |
43.53 |
43.52 |
|
|
0.34 |
0.34 |
0.34 |
0.35 |
|
|
0.35 |
0.35 |
0.35 |
0.35 |
|
|
14.95 |
14.95 |
14.95 |
16.11 |
|
|
15.51 |
15.51 |
15.51 |
16.11 |
Заключение
Из графиков на рис. 4 видно, что макросвойства композита зависят от коэффициента армирования не линейно. Функции зависимостей для материалов, армированных решетками разной формы, различаются существенно.
Различие модулей Юнга в плоскости Oxy макроматериалов, для двух форм решеток, терагональной и гексагональной, при одном и том же коэффициенте армирования, достигает 20% (рис. 4а). Различие коэффициентов Пуассона![]() достигает 30% (рис. 4б). Коэффициенты Пуассона
достигает 30% (рис. 4б). Коэффициенты Пуассона![]() и модули сдвига
и модули сдвига![]() для обоих типов решеток практически совпадают (рис. 4в, 4д). Различие коэффициентов Пуассона
для обоих типов решеток практически совпадают (рис. 4в, 4д). Различие коэффициентов Пуассона![]() достигает 48% (рис. 4г). Различие модулей сдвига
достигает 48% (рис. 4г). Различие модулей сдвига![]() достигает 24% (рис. 4д).
достигает 24% (рис. 4д).
Из таблицы (1) вино, что макросвойства композитного материала, армированного тетрагональной сеткой, с коэффициентом армирования 0.009975, рассчитанные при помощи различных методов, отличаются от среднего арифметического свойств материалов входящих состав композита не существенно (7% для ![]() ). Следовательно, в данном случае, т.е. в случае примера, взятого из работ [3], [4], для получения истинных макросвойств композита достаточно вычисления среднего арифметического свойств материалов, входящих в его состав, без решения каких-либо вспомогательных задач, возникающих в рамках используемой модели.
). Следовательно, в данном случае, т.е. в случае примера, взятого из работ [3], [4], для получения истинных макросвойств композита достаточно вычисления среднего арифметического свойств материалов, входящих в его состав, без решения каких-либо вспомогательных задач, возникающих в рамках используемой модели.
Рецензенты:
Острейковский В.А., д.т.н., профессор кафедры информатики и вычислительной техники СурГУ, ГБОУ ВПО Сургутский государственный университет ХМАО – Югры, г. Сургут.
Нехорошев В.П., д.т.н., профессор кафедры химии СурГУ, ГБОУ ВПО Сургутский государственный университет ХМАО – Югры, г. Сургут.
Библиографическая ссылка
Горынин Г.Л., Власко А.Ф. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МЕХАНИЧЕСКИХ МАКРОСВОЙСТВ МАТЕРИАЛОВ, АРМИРОВАННЫХ ПЕРИОДИЧЕСКИМИ РЕШЕТКАМИ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=17026 (дата обращения: 02.07.2025).



