Структура активной системы виброзащиты.
Рассмотрим роботизированную виброзащитную платформу, предназначенную для защиты технологических объектов, а также человека-оператора от низкочастотных воздействий со стороны подвижного основания.[1] В качестве приводного механизма использован электромеханический исполнительный механизм, который является наиболее простым по своему конструктивному исполнению и эксплуатационным характеристикам. В качестве датчиков обратных связей использованы акселерометры, установленные на объекте и основании, и датчик относительного перемещения.
Применение гибридного шагового двигателя в системе привода позволяет с высокой точностью преобразовывать цифровой электрический сигнал непосредственно в дискретные угловые перемещения (шаги) ротора.[2]
На рис. 1 представлено поперечное сечение однопакетного реактивного двигателя. Сердечник статора имеет шесть выступающих зубцов, в то время как ротор всего четыре. Сердечники как ротора, так и статора выполнены из магнитомягкой стали. Три набора обмоток расположены, как показано на рис. 1. Каждый набор состоит из двух катушек, соединенных последовательно. Набор обмоток называется фазой, и, соответственно, машина — трехфазным двигателем.
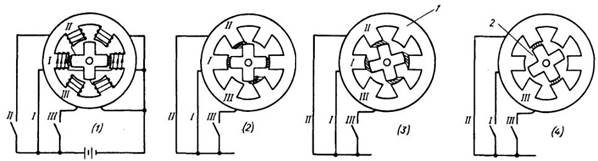
Рис. 1. Принцип работы шагового двигателя: 1 — сердечник статора; 2 — сердечник ротора.
Двигатель поворачивается за каждый импульс управления на определенный фиксированный угол. Чем меньше шаг, тем большая частота вращения может быть достигнута. Шаговые двигатели могут обеспечить маленький шаг (до 1000 шагов за один оборот)
Частота вращения задается числом шагов в секунду, и вместо показателя «частота вращения» часто используется термин «шаговая частота вращения». Однако шаговая частота вращения не определяет точно абсолютную частоту вращения.[3] Соотношение между частотой вращения и шаговой частотой вращения задается формулой
![]()
где ![]() — частота вращения, об/мин;
— частота вращения, об/мин; ![]() — шаговая частота вращения;
— шаговая частота вращения; ![]() — число шагов.
— число шагов.
Разработка математической модели. Упрощенная схема такой системы виброзащитной роботизированной платформы представлена на рис. 2. Электрические сигналы с акселерометров и датчика относительного перемещения поступают в регулятор, сигнал из которого подается на вход электрической следящей системы, управляющей поворотом ротора двигателя. Двигатель вращает винт, и гайка перемещается в направляющем элементе, изменяя положение объекта относительно основания. 4.
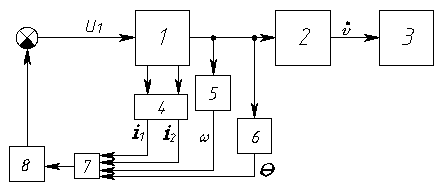
Рис. 2. Схема системы виброзащиты с электромеханическим исполнительным механизмом: 1 — электродвигатель; 2 — шарико-винтовая пара; 3 — объект виброзащиты; 4 — датчик тока; 5 — датчик скорости; 6 — датчик положения; 7 — регулятор; 8 — усилитель мощности
Построим математическую модель системы виброзащиты с учетом характеристик электромеханического приводного механизма, включающего шариковую винтовую передачу и шаговый двигатель.
В шариковой винтовой паре модель передачи скоростей и момента описывается выражениями[4]
![]()
![]()
![]() (1)
(1)
где ![]() — передаточное число по скоростным параметрам,
— передаточное число по скоростным параметрам, ![]() — передаточное число по силовым параметрам,
— передаточное число по силовым параметрам, ![]() — скорость вращения якоря двигателя,
— скорость вращения якоря двигателя, ![]() — вращающий момент на гайке,
— вращающий момент на гайке, ![]() — сила сопротивления,
— сила сопротивления, ![]() — масса платформы,
— масса платформы, ![]() — абсолютное перемещение объекта,
— абсолютное перемещение объекта, ![]() — абсолютное перемещение основания,
— абсолютное перемещение основания, ![]() — относительное перемещение объекта.
— относительное перемещение объекта.
Момент, приложенный к валу двигателя и усилие, создаваемое поступательным движением объекта, связаны зависимостью
![]() (2)
(2)
где ![]() — диаметр окружности, на которой располагаются центры шариков,
— диаметр окружности, на которой располагаются центры шариков, ![]() — угол подъема винтовой линии по цилиндру диаметром
— угол подъема винтовой линии по цилиндру диаметром ![]() ,
, ![]() — приведенный угол трения качения.[5]
— приведенный угол трения качения.[5]
С учетом выражений (1), (2), и того, что 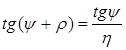 ;
; ![]() получаем передаточные отношения по скоростным и силовым параметрам
получаем передаточные отношения по скоростным и силовым параметрам
![]()
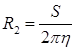 (3)
(3)
где ![]() — шаг резьбы,
— шаг резьбы, ![]() — число заходов резьбы,
— число заходов резьбы, ![]() — КПД шариковой винтовой пары.
— КПД шариковой винтовой пары.
Рассмотрим двухфазный шаговый электродвигатель с активным неявнополюсным ротором (рис. 3).
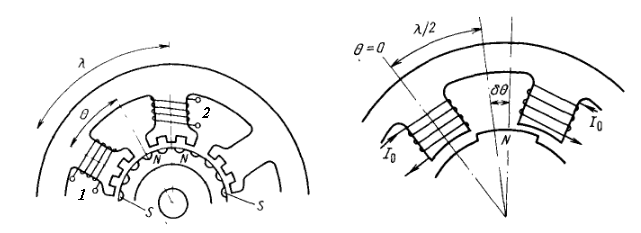
Рис. 3. Модель шагового двигателя
Примем за начало отсчета угла ![]() положение, при котором ось полюса ротора совпадает с осью первой фазы. При этом
положение, при котором ось полюса ротора совпадает с осью первой фазы. При этом ![]() ;
; ![]() ;
; ![]()
Запишем уравнения движения ротора и напряжения в обмотках статора
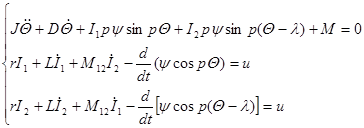 (4)
(4)
где ![]() — момент инерции ротора двигателя,
— момент инерции ротора двигателя, ![]() — ток и сопротивление 1‑й фазы статора,
— ток и сопротивление 1‑й фазы статора, ![]() — ток и сопротивление 2–й фазы статора,
— ток и сопротивление 2–й фазы статора, ![]() — напряжение источника питания,
— напряжение источника питания, ![]() — угол между осью полюсов и вектором н. с.,
— угол между осью полюсов и вектором н. с., ![]() — число пар полюсов,
— число пар полюсов, ![]() — максимальное потокосцепление возбужденного ротора с одной фазой статора,
— максимальное потокосцепление возбужденного ротора с одной фазой статора, ![]() — собственная индуктивность,
— собственная индуктивность, ![]() — коэффициент вязкого трения,
— коэффициент вязкого трения, ![]() — установившееся значение тока в обмотках,
— установившееся значение тока в обмотках, ![]() — интервалы между обмотками,
— интервалы между обмотками, ![]() — взаимная индуктивность.
— взаимная индуктивность.
Уравнения системы (4) являются нелинейными дифференциальными уравнениями. Так как нелинейные дифференциальные уравнения крайне сложно решить аналитически, линеаризуем их следующим образом. Если по обмоткам обеих фаз проходит постоянный ток ![]() , то положение равновесия здесь достигается при
, то положение равновесия здесь достигается при ![]() . Отклонение от положения равновесия обозначим
. Отклонение от положения равновесия обозначим ![]() . Оно является функцией времени t и в последующем анализе является достаточно малой величиной. Когда ротор поворачивается или колеблется, ток в обеих обмотках отклоняется от установившегося значения на
. Оно является функцией времени t и в последующем анализе является достаточно малой величиной. Когда ротор поворачивается или колеблется, ток в обеих обмотках отклоняется от установившегося значения на ![]() и
и ![]() соответственно.
соответственно.
Предположим, что
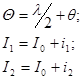 (5)
(5)
тогда имеем
![]() (6)
(6)
Учитывая, что произведение ![]() достаточно малая величина, получим
достаточно малая величина, получим
![]()
Уравнение (6) упрощается и принимает вид
![]() (7)
(7)
Тогда
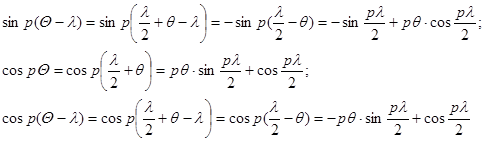 (8)
(8)
Подставив уравнения (5), (7) и (8) в (4) и приняв ![]() и
и ![]() , получим
, получим
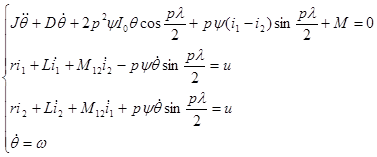 (9)
(9)
С учетом (1), (3), (4) система уравнений (9) принимает вид
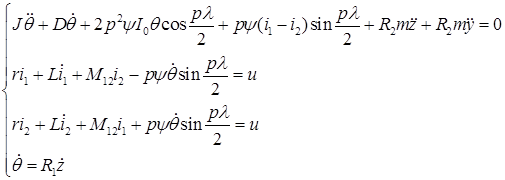 (10)
(10)
Упростим уравнения системы (10) и приведем их к виду, характерному для уравнений, описывающих систему в пространстве состояний, приняв ![]() и
и ![]() .
.
Введем 4 переменные состояния: ![]() ,
, ![]() ,
, ![]() и
и ![]() . Система уравнений (10) примет вид
. Система уравнений (10) примет вид
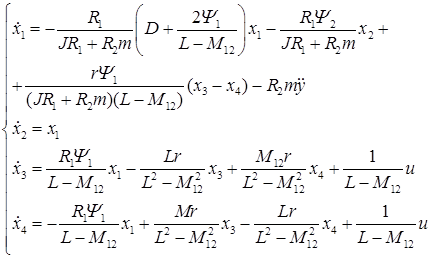
или в векторно-матричной форме
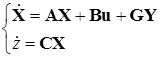
где ![]() — вектор переменных состояния,
— вектор переменных состояния, ![]() — вектор возмущающего воздействия,
— вектор возмущающего воздействия, ![]() — вектор входных сигналов A,B,C.
— вектор входных сигналов A,B,C.
От описания системы в пространстве состояний перейдём к передаточной функции, описывающей влияние напряжений на статоре ![]() на относительную скорость поступательного движения механизма
на относительную скорость поступательного движения механизма ![]()
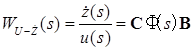
где ![]() — переходная матрица состояния,
— переходная матрица состояния, ![]() — единичная матрица.
— единичная матрица.
После проведения соответствующих вычислений можно получить передаточную функцию, описывающую влияние напряжения на статоре ![]() на угловую скорость вращения вала двигателя
на угловую скорость вращения вала двигателя ![]()
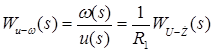
После проведения соответствующих вычислений получим передаточную функцию в виде
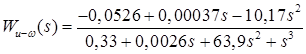
Для данной системы получим выражения для переходной характеристики, как реакции на единичное ступенчатое воздействие и частотных характеристик (АЧХ и ФЧХ) соответственно
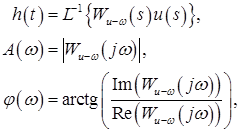 ,
,
где ![]()
Реакция полученной системы на единичное ступенчатое воздействие приведена на рис. 4, а АЧХ и ФЧХ — на рис. 5.
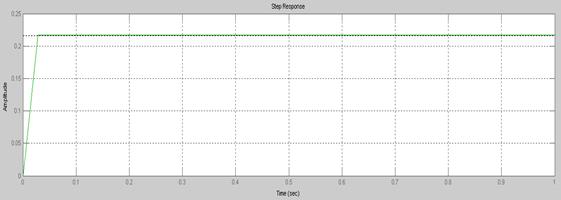
Рис. 4. Реакция рассматриваемой системы на единичное ступенчатое воздействие.
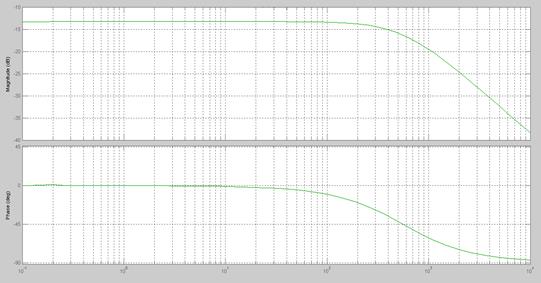
Рис. 5. Частотные характеристики (АЧХ и ФЧХ).
Из приведенных рисунков видно, что время переходного процесса при единичном ступенчатом воздействии составляет 0,0028 с, а полоса пропускания — до 500 Гц. Необходимо заметить, что колебательный характер процесса, вытекающий из вида передаточной функции, практически не проявляется из-за большой величины затухания, что является отличительной особенностью шагового двигателя.
Рецензенты:
Дуюн Т.А., д.т.н., профессор, заведующий кафедрой технологии машиностроения ФГБОУ ВПО Белгородского государственного технологического университета, г. Белгород;
Пелипенко Н.А., д.т.н., профессор Белгородского государственного национального исследовательского университета, г. Белгород.
Библиографическая ссылка
Рыбак Л.А., Черкашин Н.Н., Гунькин А.А., Чичварин А.В. МОДЕЛИРОВАНИЕ ЭЛЕКТРОМЕХАНИЧЕСКОГО ПРИВОДА С ГИБРИДНЫМ ШАГОВЫМ ДВИГАТЕЛЕМ РОБОТИЗИРОВАННОЙ ПЛАТФОРМЫ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=17012 (дата обращения: 07.07.2025).



