Цель исследования - рассмотрение потенциала различных приемов использования интерактивной доски при обучении решению текстовых задач алгебраическим методом.
Материал и методы исследования. Для решения поставленных задач и проверки исходных положений в исследовании был использован комплекс методов: методы педагогического конструирования; теоретический анализ и обобщение педагогических, психологических, методических трудов по проблеме исследования; изучение и обобщение инновационного педагогического опыта; педагогический эксперимент.
Результаты
Под текстовой задачей мы понимаем описание некоторой ситуации (явления, процесса) на естественном и/или математическом языке с требованием либо дать количественную характеристику какого-то компонента этой ситуации (определить числовое значение некоторой величины по известным числовым значениям других величин и зависимостям между ними), либо установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения, либо найти последовательность требуемых действий.
Методике обучения учащихся средней школы решению текстовых задач посвящены работы многих исследователей, данный вопрос неоднократно поднимался в отечественной дидактике обучения математике. Так В.Г. Болтянский, Л.В. Виноградова, В.А. Далингер, К.С. Муравин и Г.К. Муравин, Ф.А. Орехов, Д. Пойа, В.Ф. Чаплыгин, В.Я. Шевцов и др. исследовали потенциал различных методов решения текстовых задач в обучении математике и развития интеллектуальной сферы школьников. Г.В. Дорофеев, И.В. Дробышева, К.К. Ким, И.В. Микляева, Н.К. Рузин и др. изучают влияние текстовых задач на мотивацию учебной деятельности учащихся, а В.П. Радченко, Г.Е. Крейдлин и А.Д. Шмелев исследуют проблему языкового анализа условия текстовой задачи как средства развития продуктивного мышления. Вопросы повышения эффективности обучения решению текстовых задач средствами моделирования рассматриваются в работах А.Г. Грекуловой, К.А. Загородных, М.Т. Кац, И.А. Мешковой, А.Я. Цукаря и др. Анализ указанных работ позволил нам сделать вывод, что работа с текстовыми задачами осуществляется при традиционной классно-урочной системе. В современных условиях актуализировалась проблема обучения решению текстовых задач с использованием информационно-коммуникационных технологий.
В данной статье представлены отдельные приемы использования интерактивной доски при обучении учащихся девятых классов решению текстовых задач на процессы алгебраическим методом, которые являются частью процессуального компонента методики дифференцированного обучения решению текстовых задач алгебраическим методом с использованием интерактивных компьютерных средств. Данная методика прошла длительную апробацию в школах Волгограда и Волгоградской области.
Мы исходим из того, что текстовая задача представляет собой словесную модель ситуации, в которой описываются лишь количественные и функциональные характеристики процессов или явлений. Поэтому можно для задач на процессы унифицировать систему вопросов, регламентирующую поиск пути решения и составление математической модели задачи в виде уравнения, неравенства или их систем.
Продемонстрируем работу с задачей (*): из пункта А в пункт В одновременно отправились два автобуса. Скорость одного из них на а км/ч меньше скорости другого, а поэтому он прибыл в В на b часов позже. Найдите скорость первого автобуса, если расстояние АВ=с. Решение задачи можно найти из системы уравнений:
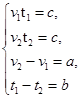 (1)
(1)
где v1 и v2 – соответственно скорости автобусов, t1 и t2 – время, затраченное ими на весь путь.
Каждое уравнение системы (1) можно изобразить с помощью графа (рис. 1) (идея исследования структур текстовых задач с использованием «трехчленного графа» была предложена Л.М. Фридманом [1]), тогда последовательно появляется граф (2):

Рис. 1. Граф к задаче (*).
«Затемненные» вершины графа соответствуют известным в задаче значениям величин. Если на ребре графа две «затемненные» вершины, то, значит, значение третьей всегда можно найти, как неизвестный компонент действия.
Начинать движение по ребрам графа следует с таких ребер модели, где есть две «затемненные» вершины. Если таковых нет, то надо вводить переменную и считать, что эта вершина также «затемненная». В нашем случае – граф (3):
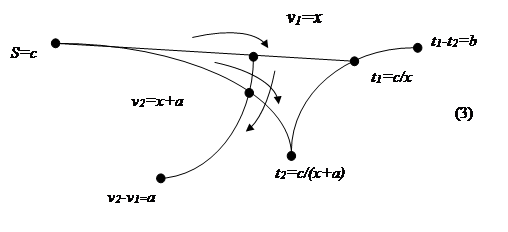
Рис. 2. Иллюстрация «движения» по ребрам графа.
Стрелками указано «движение» по ребрам графа. В результате все вершины на схеме становятся «затемненными», однако одно ребро осталось неиспользованным (без стрелки) ![]() или
или ![]() . Поиск решения закончен. Работа с графом дает возможность не строить систему уравнений, при решении которой получится одно уравнение, а сразу получить это уравнение, последовательно заменяя «светлые» вершины «темными». Данная схема работы с текстовой задачей по моделированию явных и неявных связей основывается на психологической концепции Л.К. Максимова [2] по организации учебного моделирования.
. Поиск решения закончен. Работа с графом дает возможность не строить систему уравнений, при решении которой получится одно уравнение, а сразу получить это уравнение, последовательно заменяя «светлые» вершины «темными». Данная схема работы с текстовой задачей по моделированию явных и неявных связей основывается на психологической концепции Л.К. Максимова [2] по организации учебного моделирования.
Задача (**): два портальных крана, работая вместе, разгрузили баржу за 6 ч. За какое время может разгрузить баржу, работая отдельно, каждый кран, если одному из них нужно для этого на 9 ч меньше, чем другому?
– О каких и скольких процессах ведется речь в задаче? (О работе, 2 процесса.)
– Какими величинами характеризуется работа? (Производительность, время, работа.)
– Как связаны между собой эти величины? (![]() )
)
– Какие из величин известны по условию задачи? (Время совместной работы – 6 ч.)
– Каков основной вопрос задачи? (За какое время может разгрузить баржу, работая отдельно, каждый кран?)
– Что в условии задачи сказано о работе? (Одинаковая.)
– Изобразим на графе связи между величинами (рис. 3).
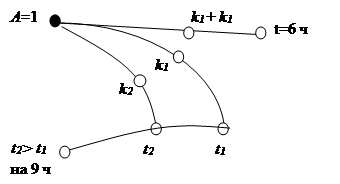
Рис. 3. Граф для задачи (**).
– Что известно о времени совместной работы двух портальных кранов? (Работая вместе, разгрузили баржу за 6 ч.)
– Что известно о времени работы портальных кранов, если они работают отдельно? (Одному из них нужно для этого на 9 ч меньше, чем другому.)
– Какую величину удобно обозначить за х?
Далее ведется работа по анализу связей между известными, принятыми за х величинами и найденными по арифметическим связям на ребрах графа.
Анализ задачного материала различных учебников алгебры для 9-го класса средней общеобразовательной школы позволил нам выделить три основных типа текстовых задач на процессы, решаемых путем составления дробно-рациональных уравнений. Работа с задачами каждого типа ведется по описанной выше схеме с использованием интерактивной доски [3]. На этом этапе работы интерактивная доска используется как средство визуализации и для повышения интенсивности представления материала. Используются эффекты анимации для появления отдельных элементов, инструмент «перо» для выполнения записей, инструмент «волшебное перо» – для привлечения внимания к пути движения по ребрам графа.
К 1-му типу отнесем следующую задачу: двое рабочих выполняли одинаковый заказ. Каждый должен был изготовить по 120 деталей за определенное время. Первый рабочий выполнил заказ на 5 часов раньше срока, так как делал на 2 детали в час больше, чем второй. Сколько деталей в час изготавливал каждый рабочий?
Решение:
![]()
![]()
![]()
![]() и
и ![]() .
.
Решая уравнение ![]() , получим два корня 6 и –8 (–8 не удовлетворяет условию задачи). Следовательно, первый рабочий изготавливал 6 дет./ч, а второй – 8 дет./ч.
, получим два корня 6 и –8 (–8 не удовлетворяет условию задачи). Следовательно, первый рабочий изготавливал 6 дет./ч, а второй – 8 дет./ч.
Ко 2-му типу отнесем задачу: на изготовление 21 детали первый рабочий затрачивает на 4 часа меньше, чем второй рабочий на изготовление 35 таких же деталей. Известно, что первый рабочий за час делает на 2 детали больше, чем второй. Сколько деталей в час делает второй рабочий?
Решение:
![]()
![]()
![]()
![]() и
и ![]() .
.
![]() ,
, ![]() ,
, ![]() (
(![]() не удовлетворяет условию задачи). Следовательно, второй рабочий делает 5 дет./ч.
не удовлетворяет условию задачи). Следовательно, второй рабочий делает 5 дет./ч.
К 3-му типу отнесем следующую задачу: два рабочих выполняли один заказ. Ежедневно первый рабочий изготавливал на 40 деталей больше, чем второй, и сделал 270 деталей. Второй рабочий работал на 2 дня больше первого и сделал 250 деталей. Сколько дней работал каждый рабочий?
Решение:
![]()
![]()
![]()
![]() и
и ![]() ,
,
![]() ,
, ![]() ,
, ![]() (
(![]() не удовлетворяет условию задачи). Следовательно, первый рабочий работал 3 дня, а второй - 5 дней.
не удовлетворяет условию задачи). Следовательно, первый рабочий работал 3 дня, а второй - 5 дней.
После того как учащиеся освоили алгоритм работы с графами при решении задач на процессы (при решении каждой из задач учитель озвучивает всю систему вопросов, сохраняя ее последовательность и структуру, фиксирует результаты поиска пути решения задачи на графе, составляет уравнение в опоре на связи между величинами, зафиксированные на графе), предлагаются различные задания на интерактивной доске.
С целью упрощения процесса изображения графа предлагается его конструировать, используя элементы, созданные с помощью инструмента «утилита множественного клонирования» (рис. 4а – используются надписи и кружки для оформления вершин графа; рис. 4б – используются надписи, кружки для оформления вершин графа, инструмент «стрелки» для иллюстрации движения по ребрам графа).
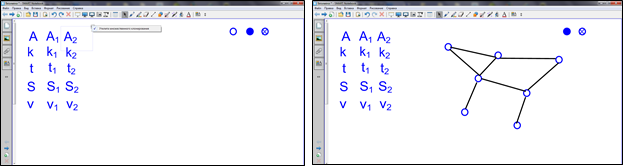
Рис. 4. Иллюстрация использования «утилиты множественного клонирования».
На последующих этапах работы по формированию умения решать задачи алгебраическим методом ученикам могут предлагаться карточки с задачами всех типов и ориентировочная схема с визуализацией типовых графов.
Карточка с задачами ([4]-[6]) всех трех типов (учащимся не предоставляется информация о типах задач):
|
1. Двое рабочих выполняли одинаковый заказ. Каждый должен был изготовить по 80 деталей за определенное время. Первый рабочий выполнил заказ на 2 час раньше срока, так как делал на 2 детали в час больше, чем второй. Сколько деталей в час изготавливал каждый рабочий? (1-й тип) 2. На изготовление 20 деталей первый рабочий затрачивает на 8 часов меньше, чем второй рабочий на изготовление 60 таких же деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час делает второй рабочий? (2-й тип) 3. Двое рабочих выполняли одинаковый заказ. Каждый должен был изготовить по 140 деталей за определенное время. Первый рабочий выполнил заказ на 3 дня раньше срока, так как делал на 6 деталей в час больше, чем второй. Сколько деталей в час изготавливал каждый рабочий? (1-й тип) 4. Два рабочих выполняли один заказ. Ежедневно первый рабочий изготавливал на 3 детали больше, чем второй, и сделал 390 деталей. Второй рабочий работал на 1 день больше первого и сделал 310 деталей. Сколько дней работал каждый рабочий? (3-й тип) 5. Два рабочих выполняли один заказ. Ежедневно первый рабочий делал на 2 детали больше, чем второй, и сделал 1560 деталей. Второй рабочий работал на 1 день больше первого и сделал 1550 деталей. Сколько дней работал каждый рабочий? (3-й тип) 6. На изготовление 63 деталей первый рабочий затрачивает на 2 часа меньше, чем второй рабочий на изготовление 72 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий? (2-й тип) |
Для учащихся с более высоким уровнем математической подготовки в карточку могут быть включены задачи других типов, которые на предыдущем этапе работы не решались, например: «На строительстве работали две бригады. После 5 дней совместной работы вторую бригаду перевели на другой объект. Оставшуюся часть работы первая бригада закончила за 9 дней. За сколько дней могла бы выполнить всю работу каждая бригада, работая отдельно, если известно, что второй бригаде на выполнение всей работы потребовалось бы на 12 дней меньше, чем одной первой бригаде?» [6].
Для организации работы по определению типа задачи и необходимой схемы графа на интерактивной доске представляется ориентировочная основа и на закладках полноразмерные схемы графов для заполнения. Ученики, проанализировав условие задачи, выбирают тип задачи и соответствующую ориентировочной основе закладку со схемой графа, которая в дальнейшем становится основой для моделирования (рис. 5). При работе с «заготовкой» графа можно использовать инструменты «перо», «стрелки», «надписи» и др. Выбор инструмента должен не усложнять работу с «заготовкой», а позволять больше внимания уделять моделированию, а не работе с интерактивной доской.
Рис. 5. Страница урока на интерактивной доске (использование закладок).
Также мы считаем эффективным прием сверки с результатом, в этом случае закладки на интерактивной доске позволяют учащимся сравнить полученный результат с образцом. При организации самостоятельной работы по решению задач можно предложить использование инструмента «шторка», за которой приготовлен образец выполнения работы. Больший эмоциональный эффект при организации проверки достигается, если не просто открывать шторку, а использовать ее различную прозрачность, высвечивая ранее приготовленный граф или решение уравнения.
В своей практике мы часто используем элементарный, на первый взгляд, прием: на интерактивной доске приготовлен окончательный вариант графа с указанием движения по ребрам, который блокируется на странице, далее цветом фона с помощью инструмента «перо» закрашивается часть или отдельные элементы, а во время работы на уроке ластиком постепенно стирается закраска, тем самым последовательно высвечивая недостающие элементы. Такая работа снижает концентрацию внимания учителя к доске, но усиливает эффект участия каждого в моделировании.
Таким образом, использование интерактивной доски позволяет повысить эффективность методики обучения учащихся девятых классов решению текстовых задач алгебраическим методом. Разнообразие приемов работы с интерактивной доской обогащает методическую систему работы учителя математики, делает ученика соавтором урока, вовлекает в поиск пути решения задачи, создает условие для моделирования и анализа. Эффективность представленных в статье приемов использования интерактивной доски оценивалась независимыми экспертами – учителями математики ряда школ Волгограда и Волгоградской области в процессе внедрения авторской методики.
Рецензенты:
Сергеев А.Н., д.п.н., профессор, зав. кафедрой информатики и информатизации образования ФГБОУ ВПО «Волгоградский государственный социально-педагогический университет», г. Волгоград;
Сахарчук Е.И., д.п.н., профессор кафедры педагогики ФГБОУ ВПО «Волгоградский государственный социально-педагогический университет», г. Волгоград.
Библиографическая ссылка
Смыковская Т.К., Машевская Ю.А., Вихляева О.М. ИСПОЛЬЗОВАНИЕ ИНТЕРАКТИВНОЙ ДОСКИ ПРИ ОБУЧЕНИИ РЕШЕНИЮ ТЕКСТОВЫХ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ // Современные проблемы науки и образования. 2014. № 6. ;URL: https://science-education.ru/ru/article/view?id=16993 (дата обращения: 17.01.2026).



